 三角比
三角比 三角比の「(90°-θ)型の変換公式」が当たり前になる考え方
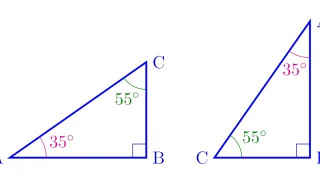
三角比sin(90°-θ), cos(90°-θ), tan(90°-θ)はいずれも,角度θの三角比sinθ, cosθ, tanθに書き直すことができます.この変換公式を用いることで,角度が揃っていない三角比も計算できることがあります.
 三角比
三角比  三角比
三角比 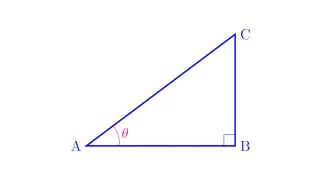 三角比
三角比  ワンステップ数学
ワンステップ数学  ワンポイント数学
ワンポイント数学 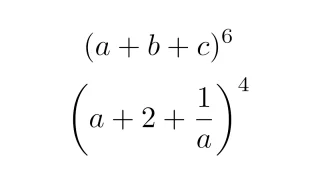 場合の数と確率
場合の数と確率  場合の数と確率
場合の数と確率 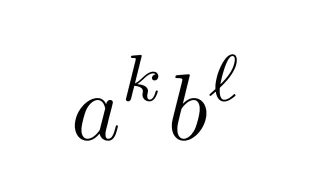 場合の数と確率
場合の数と確率  場合の数と確率
場合の数と確率  場合の数と確率
場合の数と確率