前回の記事まで因数分解の話題を中心に,2次多項式をまとめてきました.
3次以上の多項式でも因数分解のための公式がいくつかあります.
この記事では
- 3次式の因数分解の4公式
- 4次以上の因数分解の公式
をまとめます.
「多項式」の一連の記事
3次式の因数分解
3次式の展開・因数分解について,
- 4つの基本公式
- 1つの知っておくとよい公式
を紹介します.
4つの基本公式
3次式の因数分解について,次の4つの公式は基本なので確実に身につけてください.
実数$x$, $a$に対して,次の等式が成り立つ.
はじめのうちは$(x+a)^3$と$x^3+a^3$を混同しやすいので注意してください.
いずれも右辺を展開することで等しいことはすぐに分かりますね.
具体的には,
というわけですね.
$x^3+y^3+z^3-3xyz$の因数分解
次の公式は3文字の因数分解公式ですが,よく問われるので知っておきたい公式です.
実数$x$, $y$, $z$に対して,次の等式が成り立つ.
この公式も右辺を展開することで等しいことはすぐに分かりますね.
この因数分解は対称式と絡めて出題されることも意識しておくと良いでしょう.
なお,対称式とは$x$と$y$と$z$をどのように入れ替えても変化しない多項式のことをいいます.詳しくは以下の記事を参照してください.
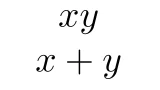
また,「3次方程式の解の公式」としてカルダノの公式というものがあり,このカルダノの公式はこの因数分解を用いて導出します.
大学入試では稀に出題される程度ですが,気になる方は大学数学の記事を執筆している姉妹ブログの以下の記事を参照してください.
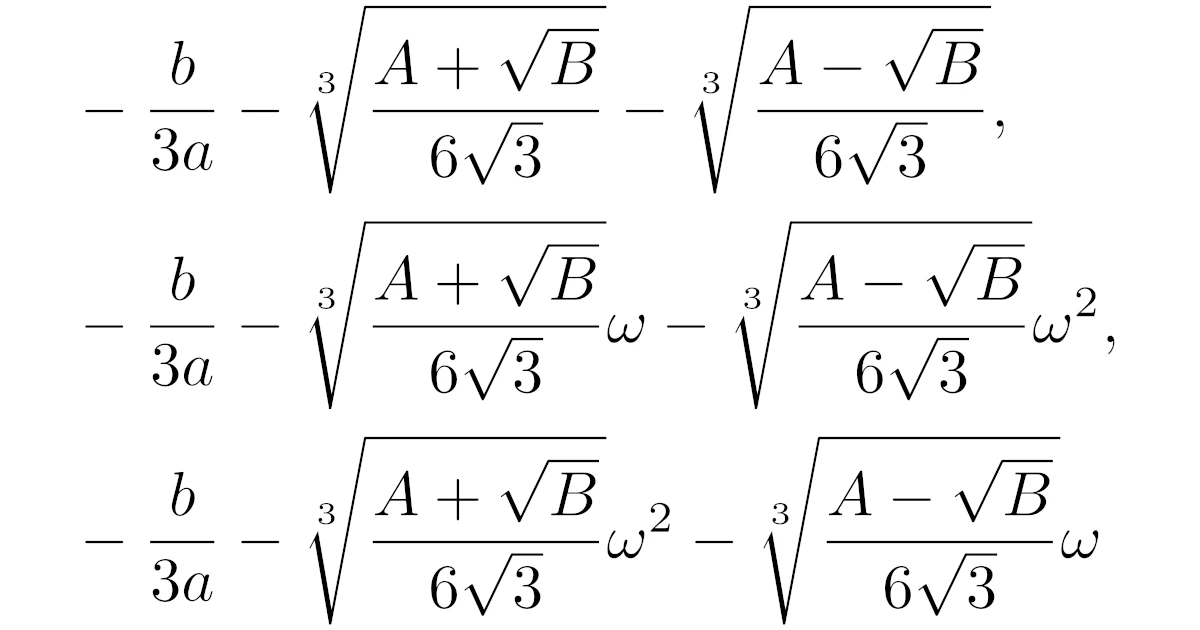
4次以上の多項式の因数分解
一般に,4次以上の因数分解では,3次式よりもさらに因数分解がしにくくなります.
複2次式の因数分解
偶数次の項のみの4次式を複2次式といいます.
複2次式はうまく2次の項を分けることで$X^2-Y^2$の形に持ち込んで因数分解できることがあります.
次を因数分解せよ.
- $x^4+x^2+1$
- $x^4-5x^4+4$
(1) $x^4+2x^2+1=(x^2+1)^2$に注目すると
となる.
(2) $x^4-4x^2+4=(x^2-2)^2$に注目すると
となる.
偶数次のみの多項式の因数分解
$x^4-10x^2+9$や$x^6-1$といった偶数次の項のみもつ多項式は,$x^2=t$などと2乗をひとつとみることで比較的因数分解できることがあります.
次を因数分解せよ.
- $x^4-10x^2+9$
- $x^6-3x^4+3x^2-1$
- $x^4-3x^2+1$
- $x^6-1$
(1) $t=x^2$とおくと,
となる.
(2) $t=x^2$とおくと,
となる.
(3) $x^4-2x^2+1=(x^2-1)^2$に注意すると,
となる.
(4) $t=x^2$とおくと,
となる.
最後の因数分解は$t=x^3$とおいても良いですね.
$x^n-y^n$の因数分解
$x^n-y^n$は
と因数分解できます.
右辺を実際に展開すれば,ほとんどの項が足し引きで消えて$x^n$と$y^n$だけが残って左辺に等しいことが分かります.
さて,この公式は$n=2$, $n=3$の場合である
- $x^2-y^2=(x-y)(x+y)$
- $x^3-y^3=(x-y)(x^2+xy+y^2)$
から連想すれば納得しやすいですね.
例えば,$n=4$の場合には
であり,$n=5$の場合には
となります.
このように$n$が$1$増えるに従って,$x^{n-1}+x^{n-2}y+\dots+y^{n-1}$の部分が増えているのが見てとれますね.
$x^n-y^n$の因数分解
$n$が奇数のとき,$x^n+y^n$は
と因数分解できます.
$x^n-y^n$の場合と同じく,右辺を実際に展開すれば,ほとんどの項が足し引きで消えて$x^n$と$y^n$だけが残って左辺に等しいことが分かります.
一方,$x^n-y^n$の場合と違うのは,実数の範囲では$n$が奇数の場合にしか因数分解ができないことです.
これは,$x^2+y^2$は実数の範囲では因数分解できませんが,$x^3+y^3$は
と因数分解できることから連想できますね.
$n=5$の場合には
となります.
$x^{n-1}-x^{n-2}y+\dots-xy^{n-2}+y^{n-1}$の部分で$+$と$-$が交互に出てくるので,最後が$+$になるためには$n$が奇数でないといけないわけですね.
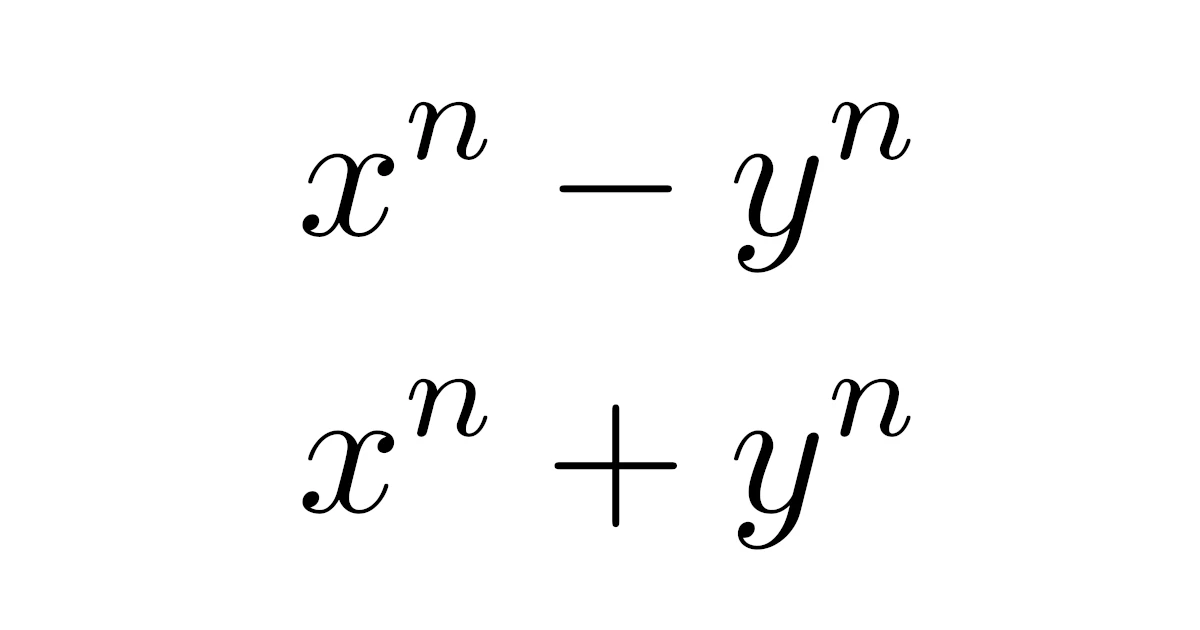
コメント