中学校で学ぶように,$y=2x+1$や$y=-x+3$のような$x$, $y$の等式は$xy$平面上の直線を表しますね.
このように,一般に$x$, $y$の等式は$xy$平面上のグラフを表しますが,そもそもグラフとはなんでしょうか?
この記事では,
- 方程式の「解」
- 方程式が表すグラフ
- グラフの平行移動
を順に説明します.
「図形と方程式」の一連の記事
$x$, $y$の方程式
方程式が表すグラフがなんなのかをきちんと整理するために,方程式の解について基本的なことを確認しておきましょう.
$x$の方程式・恒等式
文字を含んだ等式には方程式と恒等式の2種類があります.
文字$x$に関する等式について,
- 一部の$x$に対してのみ成り立つ等式を方程式
- 任意の$x$に対して成り立つ等式を恒等式
という.
具体的には,実数$x$に対して,
- $x^2-2x-3=0$はたとえば$x=0$では成り立たないので方程式
- $(x+1)(x-2)=x^2-x-2$は任意の$x$で成り立つので恒等式
というわけですね.
$x$の方程式の解
$x$の方程式は一部の$x$でしか等式を満たさないので,そのような$x$に名前を付けておくと便利そうです.これが方程式の解です.
$x$の方程式$f(x)=0$について,等式$f(a)=0$を満たす$a$をその方程式$f(x)=0$の解といい,方程式の解を全て見つけることを方程式を解くという.
要するに,方程式$f(x)=0$の未知数$x$に代入して等号が成り立つ$a$を解というだけのことですね.
たとえば,「2次方程式$x^2-2x-3=0$を解け」と言われたときは$(x-3)(x+1)=0$と左辺を因数分解して
- $x=3,-1$のときは$(x-3)(x+1)=0$を満たす
- $x\neq3,-1$のときは$(x-3)(x+1)=0$を満たさない
ということから,$x=3,-1$と答えることになるわけですね.
方程式の解とはあくまで「等式を満たすもの」であって,因数分解などは解を見つけるための手段でしかないわけですね.
$x$, $y$の方程式と解
いまのことは文字が2つ以上になっても同様です.
文字$x$, $y$に関する等式について,
- 一部の$(x,y)$に対してのみ成り立つ等式を$x$, $y$の方程式
- 任意の$(x,y)$に対して成り立つ等式を$x$, $y$の恒等式
という.また,$x$, $y$の方程式$f(x,y)=0$について,等式$f(a,b)=0$を満たす$(a,b)$を方程式$f(x,y)=0$の解といい,方程式の解を全て見つけることを方程式を解くという.
例えば,
- $x^2+y^2=1$はたとえば$(x,y)=(0,0)$では成り立たないので$x$, $y$の方程式
- $x^2+xy+y^2=(x+y)^2-xy$は任意の$(x,y)$で成り立つので$x$, $y$の恒等式
です.また,方程式$x^2+y^2=1$について
- $(x,y)=(1,0)$は$x^2+y^2=1$を満たすから解
- $(x,y)=\Bigl(-\dfrac{\sqrt{3}}{2},\dfrac{1}{2}\Bigr)$は$x^2+y^2=1$を満たすから解
- $(x,y)=(1,-2)$は$x^2+y^2=1$を満たさないから解でない
というわけですね.あくまで方程式を満たせば解で,満たさなければ解でないというだけのことです.
「方程式」と聞くと未知数が1つしか含まれていない$x^2+5x+6=0$のような等式をイメージしてしまうかもしれませんが,未知数が2つ以上含まれている$y=2x+1$や$x^3+y^2=5$のような等式も方程式と呼ぶわけですね.
方程式が表すグラフ
それでは$x$,$y$の方程式が表すグラフについて説明しましょう.
$x$, $y$の方程式$f(x,y)=0$の解を表す$xy$平面上の点を全てとってできる図を方程式$f(x,y)$が表すグラフという.
具体例をみていきましょう.
具体例1(直線)
$x$, $y$の方程式$y=\dfrac{1}{2}x+1$に対して,たとえば
- $(x,y)=(0,1)$
- $(x,y)=(2,2)$
- $(x,y)=\Bigl(-\pi,-\dfrac{1}{2}\pi+1\Bigr)$
は全て代入すれば方程式の等号を満たすので解です.
このように,方程式$y=\dfrac{1}{2}x+1$を満たす$(x,y)$を全て$xy$平面上に図示したものが方程式$y=\dfrac{1}{2}x+1$のグラフで,中学で学ぶように直線になりますね.
このグラフからも分かるように,方程式$y=\dfrac{1}{2}x+1$の解は無数にあることが分かります.
そのため,解を挙げていくとキリはありませんが,このようにグラフに図示すれば解を「視覚的に」「全て」表すことができるのでグラフは便利なわけですね.
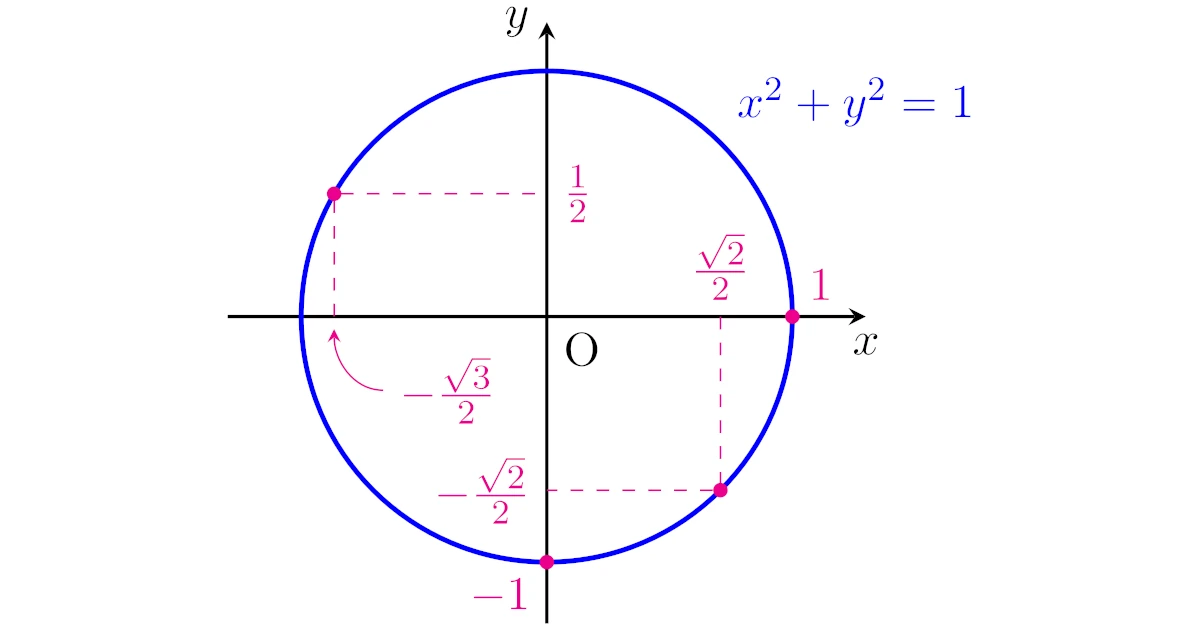
具体例2(円)
$x$, $y$の方程式$x^2+y^2=1$に対して,たとえば
- $(x,y)=(1,0)$
- $(x,y)=\Bigl(-\dfrac{\sqrt{3}}{2},\dfrac{1}{2}\Bigr)$
- $(x,y)=\Bigl(\dfrac{\sqrt{2}}{2},-\dfrac{\sqrt{2}}{2}\Bigr)$
- $(x,y)=(0,-1)$
は全て代入すれば方程式の等号を満たすので解です.
このように,方程式$x^2+y^2=1$を満たす$(x,y)$を全て$xy$平面上に図示したものが方程式$x^2+y^2=1$のグラフで,実は下図のように円になります.
グラフの平行移動
$x,y$の方程式の$xy$平面上のグラフを平行移動させてできるグラフを表す方程式がどうなるかを考えましょう.
$xy$平面上の$f(x,y)=0$のグラフを$x$軸方向,$y$軸方向にちょうど$a$, $b$だけ平行移動させたグラフの方程式は$f(x-a,y-b)=0$である.
これを示すには,
- 点$(p,q)$が方程式$f(x,y)=0$のグラフ上の点である
- 点$(p+a,q+b)$が方程式$f(x-a,y-b)=0$のグラフ上の点である
が同値であることを示せば良い.
グラフの定義より
- (1)と$f(p,q)=0$を満たすことは同値
- (2)と$f((p+a)-a,(q+b)-b)=0$を満たすことは同値
であり,
だから$(1)\iff(2)$は同値である.
要するに,$f(x,y)=0$の解が$(x,y)=(p,q)$であれば$(x,y)=(p+a,q+b)$は$f(x-a,y-b)=0$の解で,この逆も成り立つので上のように平行移動が成り立つわけですね.
たとえば,放物線$y=x^2$のグラフを
- $x$軸方向にちょうど$+2$
- $y$軸方向にちょうど$+1$
平行移動させたグラフの方程式は$y-1=(x-2)^2$ですね.
コメント