力学は高校物理で最初に学ぶ分野です.
これは物理の他の分野でも力学の知識が必要になるためで,もし高校物理で最初の力学でコケてしまうとズルズルと物理が分からなくなってしまいます.
さて,力学では力や速度といった向きと大きさを持ったものを表すために「矢印」を用います.
この「矢印」はベクトルと呼ばれ,本来ベクトルは数学で学ぶものですが,高校物理で扱うベクトルは基本的な部分に限られるので力学の分野で簡単に学ぶことになります.
この記事では,ベクトルの基本事項として
- ベクトルとは何か?
- ベクトルの和
- ベクトルの分解
を順に説明し,最後に物理におけるベクトルの使用例を紹介します.
「力学の基本」の一連の記事
ベクトル
ここではベクトルの基本事項を説明します.
ベクトルとは何か?
向きと大きさを併せたものをベクトルという.
このベクトルは矢印で表すことが多く,矢印の「矢の側」を終点,「矢の反対側」を始点という.
高校物理,高校数学では,ベクトルは$\ve{a}$のように上に矢印をつけて表します.
さて,ベクトルは「向きと大きさを併せたもの」なので,どこにあろうが平行移動させてぴったり一致するならば,それらは同じベクトルということになります.
2つのベクトル$\ve{a}$, $\ve{b}$に対して,それぞれのベクトルを表す矢印を平行移動させて一致するとき$\ve{a}=\ve{b}$と表す.
よって,下図のベクトルは全て同じベクトルですね.
つまり,直感的にはベクトルは平行移動させてもよい矢印だと思って問題ありません.
ベクトルの和
次に,2つのベクトルの和を考えましょう.
平面(または空間)上の2点$\mrm{A}$, $\mrm{B}$に対して,$\mrm{A}$を始点とし$\mrm{B}$を終点とするベクトルを$\Ve{AB}$と表す.
このベクトルの表し方を用いて,ベクトルの和を次のように定義します.
平面(または空間)上の3点$\mrm{A}$, $\mrm{B}$, $\mrm{C}$に対して,$\Ve{AB}$と$\Ve{BC}$の和$\Ve{AB}+\Ve{BC}$を
と定める.
つまり,ベクトル$\ve{a}$, $\ve{b}$の和$\ve{a}+\ve{b}$とは,$\ve{a}$の終点に$\ve{b}$の始点を繋げてできるベクトルというわけですね.
また,ベクトルの和はいま定義した通りですが,ベクトルの差$\ve{a}-\ve{b}$は次のように定義されます.
$\ve{a}$と大きさが等しく,逆向きのベクトルを$\ve{a}$の逆ベクトルといい$-\ve{a}$で表す.
また,$\ve{a}+(-\ve{b})$を$\ve{a}$から$\ve{b}$を引いた差といい$\ve{a}-\ve{b}$と表す.
実数で$5+(-3)$を$5-3$と書くのと同じですね.
ベクトルの分解
ベクトル$\ve{c}$を考えます.
このとき,下図のように$\ve{c}$が対角線になる平行四辺形を考えれば,$\ve{c}=\ve{a}+\ve{b}$となるようなベクトル$\ve{a}$, $\ve{b}$に分解することができますね.
このように,ベクトルの和とは逆に1つのベクトルを2つ以上のベクトルに分解することをベクトルの分解といいます.
ただし,上の図でも$\ve{c}$が対角線になる平行四辺形はいくつも考えられるので,ベクトルの分解はいくつも考えられますね.
そのため扱いやすいようにベクトルを分解することが大切ですが,そこまで技巧的な分解が必要な場面はまずありません.
ベクトルの例
物理でベクトルを使う基本的な例としては力と速度が挙げられます.
力
力学では物体にはたらく力を理解することが大切で,
- 力の作用点
- 力の大きさ
- 力の向き
の3つを併せて力の三要素と呼ばれます.この力の三要素は
- どの点に
- どれくらいの大きさの力が
- どの向きに
はたらいているのかということで,確かに大切そうだということは直感的にも難しくないですね.
普通ベクトルは平行移動して一致するものは等しいと考えますが,作用点を気にする場合にはベクトルの始点を作用点にとって表します.
例えば,床に置かれた物体を糸で引っ張る場合,この物体を引く力$\ve{F}$は下図のように表します.
このようにベクトルを用いることで力の三要素を視覚的に表すことができるわけですね.
速度
物理では速さと速度の意味が異なります.きちんと使い分けることが大切です.
「時間当たりの移動距離」を速さといい,「速さと向き」を併せて速度という.
例えば「東に時速$3\mrm{km}$で歩き,折り返して西に時速$3\mrm{km}$で歩いた」とき,これはずっと時速$3\mrm{km}$の「速さ」で歩いたと言えます.
一方,速度は向きを含めて考えるので,向きが変化しているため,これはずっと時速$3\mrm{km}$の「速度」で歩いたとは言えません.
この「速さ」と「速度」の使い分けは物理のルールなので,確実に区別して理解しておいてください.
速さは英語で“speed”,速度は英語で“velocity”です.
このように考えると
- 「速さ」をベクトルの大きさ
- 「進む方向」をベクトルの向き
で表すことにより,速度はベクトルで表すのが良さそうです.
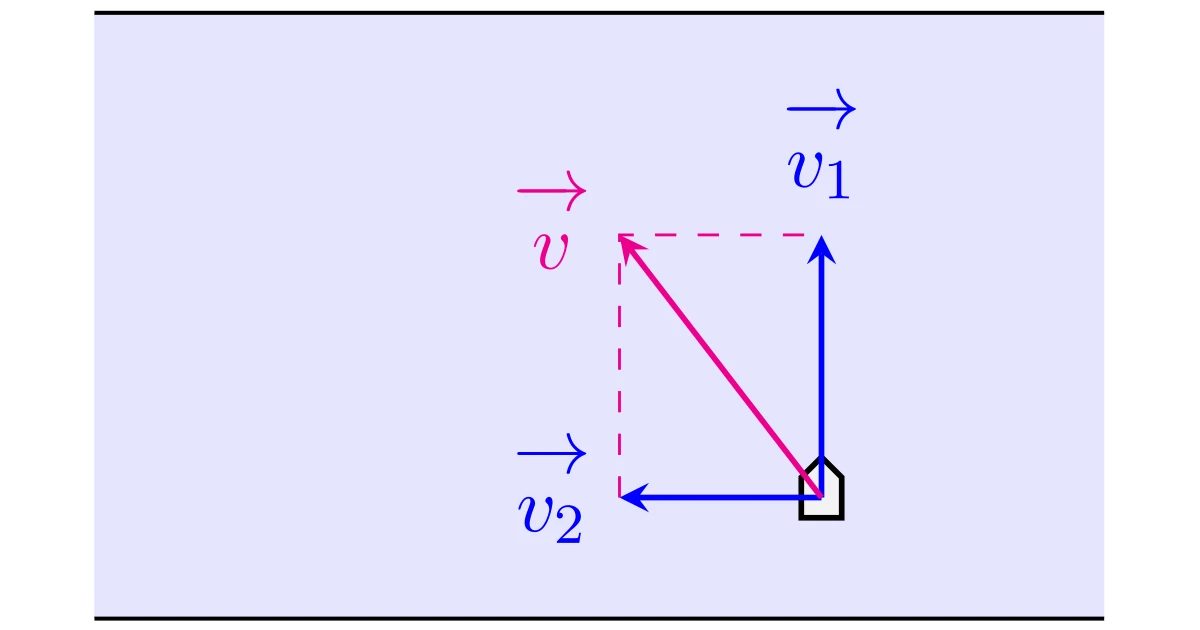
例えば,一定の速度で水が流れている川を船で渡るとき,船を川に垂直に漕ぐと流されながら船が進んでいきます.このときの船の速度は下図のように表せますね.
つまり,船の速度$\ve{v}$は川の速度$\ve{v_1}$と流れがないときの船の速度$\ve{v_2}$によって,$\ve{v}=\ve{v_1}+\ve{v_2}$と表されますね.
コメント