例えば
のような三角関数を1種類のみ含む方程式・不等式は$\sin{\theta}$や$\cos{\theta}$について解いて考えれば良いのでした.
次の問題はどのように解けばいいでしょうか?
$\theta$の方程式$\sin{\theta}-\sqrt{3}\cos{\theta}=-1$($0\leqq\theta<2\pi$)を解け.
実はこの方程式の左辺で三角関数の加法定理を用いれば,$2\sin{\bra{\theta-\dfrac{\pi}{3}}}=0$の形にまとめることができ,方程式を解くことができます.
このように$A\sin{\theta}+B\cos{\theta}$の形に三角関数の加法定理を用いて
と1つの三角関数にまとめて表すことを三角関数の合成といいます.
この記事では
- 三角関数の合成の考え方
- $\sin$への合成の具体例
- 三角関数の合成の応用
- $\cos$への合成の考え方・具体例
を順に説明します.
「三角関数」の一連の記事
三角関数の合成の考え方
三角関数の合成の基本の考え方を説明してから,一般の三角関数の合成を説明します.
基本の考え方
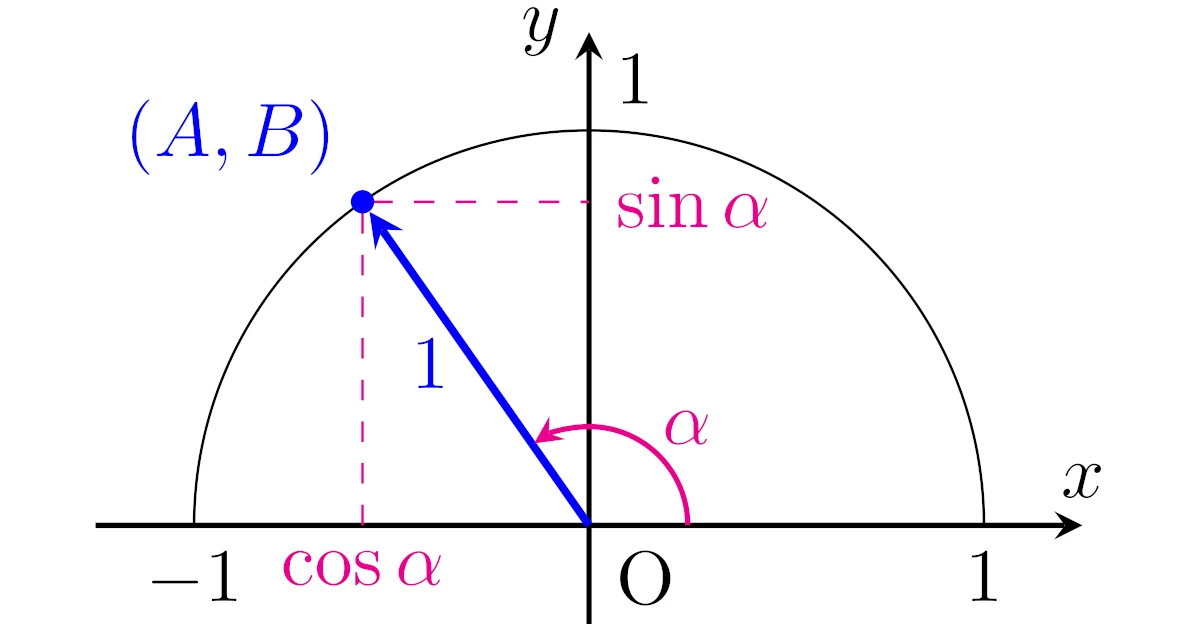
実数$A$, $B$が$A^2+B^2=1$を満たすとして,このときに$A\sin{\theta}+B\cos{\theta}$を$\sin{(\theta+\alpha)}$の形に合成しましょう.
このとき,$xy$平面上の点$(A,B)$は単位円周上に存在しますから,点$(A,B)$の$x$軸正方向からの偏角を$\alpha$とすると,三角関数の定義から
となりますね.
このとき,$A\sin{\theta}+B\cos{\theta}$は三角関数($\sin$)の加法定理を用いると,
とひとつの三角関数にまとめることができますね.
一般の場合の考え方
いまは実数$A$, $B$が$A^2+B^2=1$を満たしている場合でしたが,$A^2+B^2=1$を満たしていなくても少し工夫すれば三角関数の合成が使えます.
少なくとも一方は0でない実数$A$, $B$に対して,$A\sin{\theta}+B\cos{\theta}$を$C\sin{(\theta+\alpha)}$の形に合成しましょう.
$C=\sqrt{A^2+B^2}$とおくと
となります.つまり,$A’=\dfrac{A}{C}$, $B’=\dfrac{B}{C}$とおくと$A’^2+B’^2=1$を満たします.よって,
とおくことができますね.
そこで,$C$でくくったあとに三角関数の加法定理($\sin$の加法定理)を使えば
とひとつの三角関数にまとめることができますね.
$\sin$への合成の具体例
いまの考え方でみたように,
- $C=\sqrt{A^2+B^2}$で$A\sin{\theta}+B\cos{\theta}$をくくる
- $\dfrac{A}{C}=\cos{\alpha}$, $\dfrac{B}{C}=\sin{\alpha}$とおいて三角関数の加法定理を使う
の2ステップで三角関数の合成ができますね.
具体例1($\frac{1}{2}\sin{\theta}+\frac{\sqrt{3}}{2}\cos{\theta}$)
$\dfrac{1}{2}\sin{\theta}+\dfrac{\sqrt{3}}{2}\cos{\theta}$を$C\sin{(\theta+\alpha)}$の形に合成せよ.
係数の2乗和は$\biggl(\dfrac{1}{2}\biggr)^2+\biggl(\dfrac{\sqrt{3}}{2}\biggr)^2=1$だから,
とおける.よって,三角関数の加法定理より
となる.いま,$(*)$を満たす$\alpha$として$\alpha=\dfrac{\pi}{3}$が具体的にとれるので,
と合成できる.
いまの解答ではいったん$\alpha$をおきましたが,慣れてくれば一気に
としても構いません.
$0\leqq\theta<2\pi$と$\alpha$に制限をつけたのは,$(*)$を満たす$\alpha$が$2\pi$ごとに無数に存在するためです.$0\leqq\theta<2\pi$とすれば,そのうちのひとつに決めまりますね.
具体例2($-\sin{\theta}+\cos{\theta}$)
$-\sin{\theta}+\cos{\theta}$を$C\sin{(\theta+\alpha)}$の形に合成せよ.
係数の2乗和は$(-1)^2+1^2=2$だから,
なので,
とおける.よって,三角関数の加法定理より
となる.いま,$(*)$を満たす$\alpha$として$\alpha=\dfrac{3\pi}{4}$が具体的にとれるので,
と合成できる.
具体例1と同様に,いまの解答ではいったん$\alpha$をおきましたが,慣れてくれば一気に
としても構いません.
具体例3(${3\sin{\theta}+4\cos{\theta}}$)
$3\sin{\theta}+4\cos{\theta}$を$C\sin{(\theta+\alpha)}$の形に合成せよ.
とおける.よって,三角関数の加法定理より
と合成できる.
具体例1と具体例2ではたまたま$\alpha$が有名角で具体的に分かりましたが,この例3のように$\alpha$が具体的に表すのが難しいこともよくあります.
三角関数の合成の応用
次に三角関数の合成がどのように応用できるかを説明します.
関数の取りうる値の範囲
$\theta$が実数全体を動くとき,関数$f(\theta)=2\sin{\theta}+3\cos{\theta}$のとりうる値の範囲を求めよ.
三角関数の和の形$A\sin{\theta}+B\cos{\theta}$のままではそれぞれが増減するので値の範囲を考えるのは難しいですが,ひとつにまとめて$C\sin{(\theta+\alpha)}$の形にしてしまえば考えやすいというわけですね.
係数の2乗和は$2^2+3^2=13$だから$\bra{\dfrac{2}{\sqrt{13}}}^2+\bra{\dfrac{3}{\sqrt{13}}}^2=1$が成り立つので,
とおける.よって,三角関数の加法定理より
と合成できる.$\theta$は実数全体を動くから$\theta+\alpha$も実数全体を動くので,$\sin{(\theta+\alpha)}$のとりうる値の範囲は$-1\le\sin{(\theta+\alpha)}\le1$である.
よって,$f(\theta)$のとりうる値の範囲は
である.
三角関数を含んだ方程式
冒頭で触れた$A\sin{\theta}+B\cos{\theta}$型の方程式・不等式を解きましょう.
$\theta$の方程式$\sin{\theta}-\sqrt{3}\cos{\theta}=-1$($0\leqq\theta<2\pi$)を解け.
係数の2乗和は$1^2+(-\sqrt{3})^2=4$だから$\biggl(\dfrac{1}{2}\biggr)^2+\biggl(-\dfrac{\sqrt{3}}{2}\biggr)^2=1$が成り立つので,
とおくことができ,このような$\alpha$として$\alpha=\dfrac{\pi}{3}$がとれる.
よって,方程式の左辺は三角関数の加法定理より
と合成できるので,方程式は
となる.ここで,$0\le\theta<2\pi$から$-\dfrac{\pi}{3}\le\theta-\dfrac{\pi}{3}<\dfrac{5\pi}{3}$であることに注意すれば,
と解ける.
$\cos$への合成
ここまでは$A\sin{\theta}+B\cos{\theta}$を$C\sin{(\theta+\alpha)}$の形に合成してきましたが,同様に考えることで$C\sin{(\theta+\beta)}$の形に合成することもできます.
$\sin$への合成と同様に,$C=\sqrt{A^2+B^2}$とおいて
と$C$でくくります.
ここで$\dfrac{A}{C}=\sin{\beta}$, $\dfrac{B}{C}=\cos{\beta}$なる$\beta$をとれば,三角関数の加法定理($\cos$の加法定理)が使えて
と合成することができますね.
具体例1($-\sin{\theta}+\cos{\theta}$)
$-\sin{\theta}+\cos{\theta}$を$C\cos{(\theta-\beta)}$の形に合成せよ.
係数の2乗和は$(-1)^2+1^2=2$だから
とおくことができ,このような$\alpha$として$\alpha=\dfrac{7\pi}{4}$がとれる.
よって,三角関数の加法定理より
と合成できる.
具体例2(${3\sin{\theta}+4\cos{\theta}}$)
$3\sin{\theta}+4\cos{\theta}$を$C\cos{(\theta-\beta)}$の形に合成せよ.
コメント