三角関数$\cos{\theta}$, $\sin{\theta}$, $\tan{\theta}$も関数ですから,これらのグラフがどうなるのかは気になるところです.
$\cos{\theta}$, $\sin{\theta}$のグラフは,定義から単位円周上で点を動かして考えることができます.
この記事では
- 三角関数$\sin{\theta}$の増減とグラフ
- 三角関数$\cos{\theta}$の増減とグラフ
- 三角関数$\tan{\theta}$の増減とグラフ
を説明します.
この記事では点Oを原点,点Pを単位円周上の偏角$\theta$の点$(\cos{\theta},\sin{\theta})$とします.
「三角関数」の一連の記事
$\sin{\theta}$の増減とグラフ
点$\mrm{P}$が単位円周上を1周するときに$\sin{\theta}$がどのように増減しているかを掴み,グラフを描きましょう.
$\sin{\theta}$の増減
点$\mrm{P}$が単位円周上を1周するとき($\theta$が$0\leqq\theta\leqq2\pi$の範囲を動くとき),以下のように$\sin{\theta}$は増減します.
[1] $0\leqq\theta\leqq\dfrac{\pi}{2}$ $(0^\circ\leqq\theta\leqq90^\circ)$のとき
$\sin{\theta}$は$0$から$1$まで増加
[2] $\dfrac{\pi}{2}\leqq\theta\leqq\dfrac{3\pi}{2}$ $(90^\circ\leqq\theta\leqq270^\circ)$のとき
$\sin{\theta}$は$1$から$-1$まで減少
[3] $\dfrac{3\pi}{2}\leqq\theta\leqq2\pi$ $(270^\circ\leqq\theta\leqq360^\circ)$のとき
$\sin{\theta}$は$-1$から$0$まで増加
よって,$\sin{\theta}$の増減表は以下のようになりますね.
| $\theta$ | $0$ | $\dots$ | $\dfrac{\pi}{2}$ | $\dots$ | $\dfrac{3\pi}{2}$ | $\dots$ | $2\pi$ |
|---|---|---|---|---|---|---|---|
| $\sin{\theta}$ | $0$ | $\nearrow$ | $1$ | $\searrow$ | $-1$ | $\nearrow$ | $0$ |
$\sin{\theta}$のグラフ
以上の増減をふまえつつ,$y=\sin{\theta}$のグラフを
で順にプロットしていきましょう.
このように点$\mrm{P}$を単位円上で動かすと,$\sin{\theta}$のグラフが下図のようになることが分かりますね.
この図からも$\theta$が$2\pi$ごとに同じ値を取ることが見てとれますね.
先ほどの$\sin{\theta}$の増減表でも見たように
- $0\leqq\theta\leqq\dfrac{\pi}{2}$で単調増加
- $\dfrac{\pi}{2}\leqq\theta\leqq\dfrac{3\pi}{2}$で単調減少
- $\dfrac{\pi}{2}\leqq\theta\leqq2\pi$で単調増加
となっていることを確認してください.
$\cos{\theta}$の増減とグラフ
点$\mrm{P}$が単位円周上を1周するときに$\cos{\theta}$がどのように増減しているかを掴み,グラフを描きましょう.
$\cos{\theta}$の増減
点$\mrm{P}$が単位円周上を1周するとき($\theta$が$0\leqq\theta\leqq2\pi$の範囲を動くとき),以下のように$\cos{\theta}$は増減します.
[1] $0\leqq\theta\leqq\pi$ $(0^\circ\leqq\theta\leqq180^\circ)$のとき
$\cos{\theta}$は$1$から$-1$まで減少
[2] $\pi\leqq\theta\leqq2\pi$ $(180^\circ\leqq\theta\leqq360^\circ)$のとき
$\cos{\theta}$は$-1$から$1$まで増加
よって,$\cos{\theta}$の増減表は以下のようになりますね.
| $\theta$ | $0$ | $\dots$ | $\pi$ | $\dots$ | $2\pi$ |
|---|---|---|---|---|---|
| $\cos{\theta}$ | $1$ | $\searrow$ | $-1$ | $\nearrow$ | $1$ |
$\cos{\theta}$のグラフ
先ほどの$\sin{\theta}$と同じように考えると,$\sin{\theta}$のグラフが下図のようになることが分かりますね.
この図からも$\theta$が$2\pi$ごとに同じ値を取ることが見てとれますね.
先ほどの$\cos{\theta}$の増減表でも見たように
- $0\leqq\theta\leqq\pi$で単調減少
- $\pi\leqq\theta\leqq2\pi$で単調増加
となっていることを確認してください.
$\tan{\theta}$の増減とグラフ
最後に$\tan{\theta}$のグラフを考えましょう.
$\tan{\theta}$の図形的意味(復習)
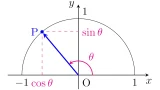
$\tan{\theta}$は直線$\mrm{OP}$と$x=1$の交点の$y$座標として得られることを思い出しておきましょう.
$\tan{\theta}$のグラフ
$y=\tan{\theta}$のグラフを
で順にプロットしていきましょう.
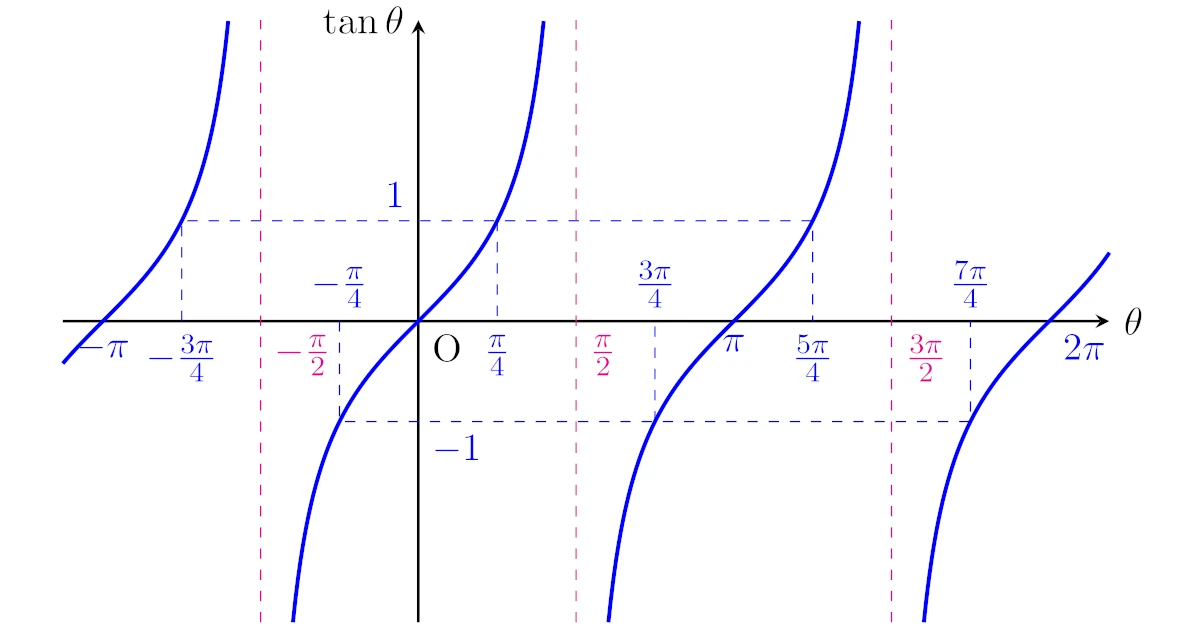
このように点$\mrm{P}$を単位円上で動かすと,$\tan{\theta}$のグラフが下図のようになることが分かりますね.
この図から$\theta$が$\pi$ごとに同じ値を取ることが見てとれますね.
また,点$\mrm{P}$が$y$軸上にあるとき$\tan{\theta}$を定義されず,$x=\dfrac{\pi}{2}+n\pi$($n$は整数)で表される直線は漸近線となりますね.
以上より,$\tan{\theta}$の増減表が以下のようになることも分かりますね.
| $\theta$ | $0$ | $\dots$ | $\dfrac{\pi}{2}$ | $\dots$ | $\dfrac{3\pi}{2}$ | $\dots$ | $2\pi$ |
|---|---|---|---|---|---|---|---|
| $\sin{\theta}$ | $0$ | $\nearrow$ | × | $\nearrow$ | × | $\nearrow$ | $0$ |
コメント