等速直線運動とその公式｜「速さ」と「速度」の違いから解説

日常的には速さや速度という言葉を同じように使いますが，物理ではこれらは明確に異なる概念です．

そのため，速さ・速度の違いを意識せずに問題を解くと，間違いになってしまうことがあります．

また，物理には等速直線運動と呼ばれる運動があり，この運動はその名の通り「同じ速度で進む運動」のことをいい，物理の中で最も基本的と言ってよい運動の１つです．

等速直線運動を理解するためには，速度をきちんと物理的な意味で理解する必要があります．

この記事では

• 速度と速さの違い
• 速度と等速直線運動

を順に説明します．

「速さ」と「速度」の違い

冒頭でも述べたように，物理では速さと速度は明確に区別されており，きちんと使い分ける必要があります．

平均の速さと瞬間の速さ

まずは

• 平均の速さ
• 瞬間の速さ

の２種類の速さを説明します．

平均の速さ

例えば，マラソンでは最初から最後まで同じスピードで走るわけではなく，他の選手との駆け引きや，ラストスパートなどで速くなったり遅くなったりします．

常に同じスピードで走っているわけではなくても，「10kmを40分で走った」というのは「全体では分速250mで走った」と考えることができますね．

つまり，途中のスピードをならして長期的なスピードを考えているわけですね．

このように，瞬間瞬間のスピードは気にせず，長期的に考えるスピードのことを平均の速さといいます．

瞬間の速さ

移動する物体を観察するとき，その観察時間が十分に短ければ，その間でスピードはほとんど変化していないと言ってよいでしょう．

この観察時間は短ければ短いほど，その間のスピードの変化はないものと考えることができ，どんどん観察時間を短くしていけば，一瞬一瞬のスピードを考えていることになりますね．

このようにして考えた瞬間のスピードのことを瞬間の速さといいます．

平均の速さを「長期的に考えるスピード」というならば，瞬間の速さは「短期的に考えるスピード」ということができますね．

速さの単位

時間の単位としては，

• 秒（記号はsecondの頭文字で“$\mrm{s}$”）
• 時間（記号はhourの頭文字で“$\mrm{h}$”）

が使われることが多く，距離の単位としてはメートル（記号はmeterの頭文字“$\mrm{m}$”）が使われることが多いです．

これらを用いると，例えば

• 「時速$3\mrm{km}$」は$3\mrm{km/h}$
• 「秒速$5\mrm{m}$」は$5\mrm{m/s}$

などと表されます．

速度と等速直線運動

次に速度と等速直線運動を説明します．

速度

速さはあくまでスピードだけですが，速度は速さに加えて移動の方向も考えます．

このため，「一定の速度で進む」と言えば，速さ・向きが一定という意味になるので向きを変えずに進むことになります．

よって，物理で「A君が一定の速度で進む」と言えば，「A君は道が曲がっていても関係なく，壁にぶつかろうが側溝に落ちようがお構いなしに，壁をぶち破ったり側溝の水の中をじゃぶじゃぶと『まっすぐ』進む」ことになります．

速度は向き・大きさを同時に考えているので，矢印（ベクトル）で図示することができますね．

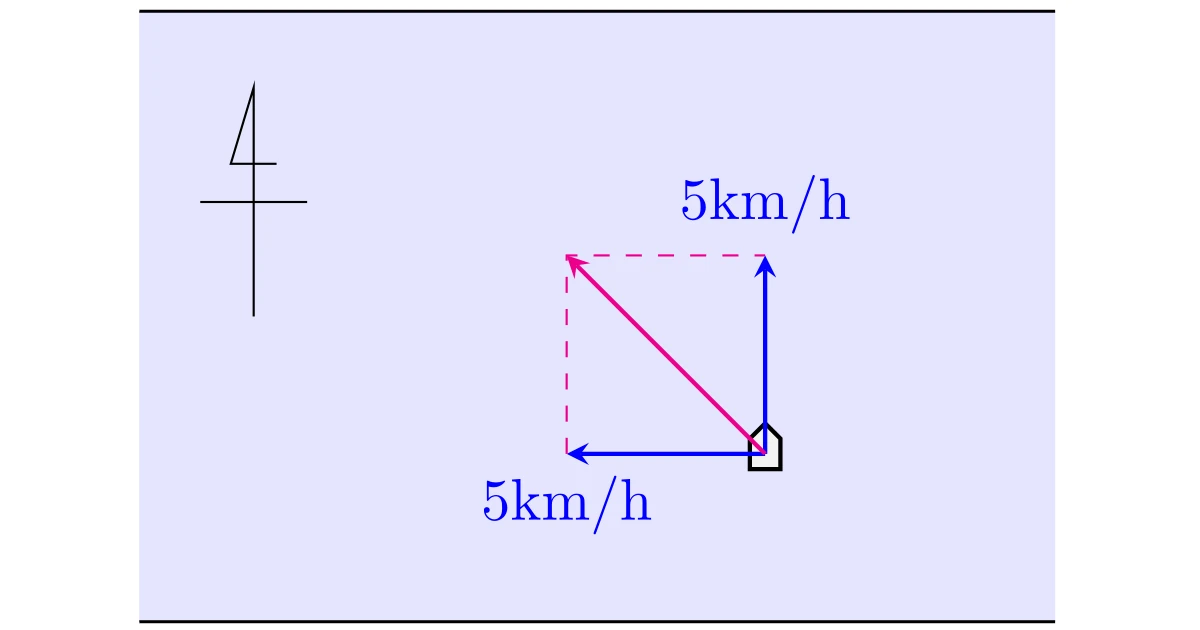
例えば，下図のように$5\mrm{km/h}$で東から西へ流れている川を，静水中で$5\mrm{km/h}$の速さで進む船が北に進もうとするとき，船は流されて北西の方角へ進みます．

このとき，実際に進む船の速さは三平方の定理から$5\sqrt{2}\mrm{km/h}$となります．

以上より，実際に進む船の速度は

• 北西の方角へ
• 速さ$5\sqrt{2}\mrm{km/h}$

となります．このように，方向と大きさを併せて初めて速度と言えることに注意してください．

等速直線運動と公式

スケートを思い浮かべると分かるように，氷の上は滑りやすいことを私たちは知っています．これは氷上とストーンの間の摩擦力は非常に小さいためで，氷の上を滑る物体はほとんど一定の速度で滑っていきます．

現実には摩擦力は0ではないのでいずれ物体は静止しますが，もし摩擦力（や空気抵抗など）が完全に0であれば物体は止まることなく一定の速度で移動します．

このような運動のことを等速直線運動といいます．

上で説明したように速度は速さと向きを併せたものでしたから，「一定の速度で移動する」とは「同じ方向に一定の速さで移動する」と言っても同じことですね．

小学校以来学んできたように，等速直線運動における速さ・時間・距離には次の関係があります．

距離$x$は時間$t$と速さ$v$に比例すると言ってもよいですね．