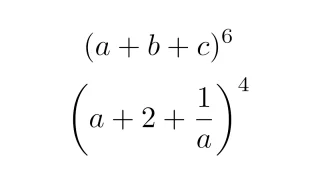 場合の数と確率
場合の数と確率 場合の数9
(a+b+c)ⁿの展開は多項定理!考え方と具体例
(a+b)ⁿの展開公式である二項定理に対して,(a+b+c)ⁿや(a+b+c+d)ⁿなど( )の中の項が3つ以上のときの展開公式を多項定理といいます.この記事では多項定理が重複順列から導けることを説明し,多項定理の具体例を紹介します.
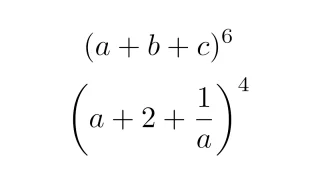 場合の数と確率
場合の数と確率 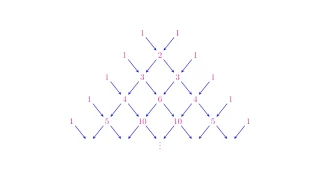 場合の数と確率
場合の数と確率 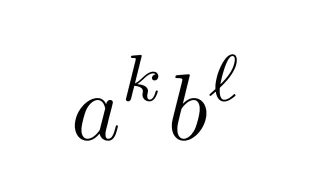 場合の数と確率
場合の数と確率 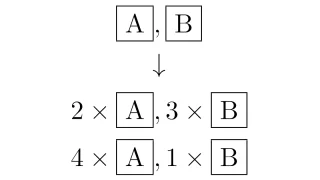 場合の数と確率
場合の数と確率 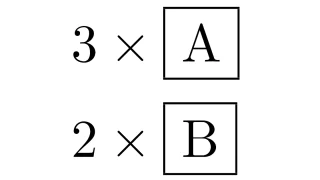 場合の数と確率
場合の数と確率  場合の数と確率
場合の数と確率 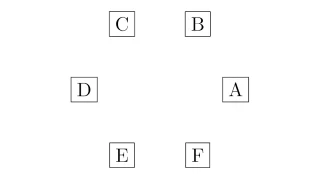 場合の数と確率
場合の数と確率  場合の数と確率
場合の数と確率 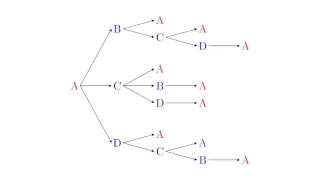 場合の数と確率
場合の数と確率  場合の数と確率
場合の数と確率