「図形と方程式」の一連の記事
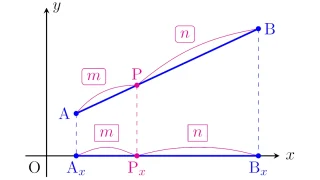
- 1 座標の超基本「内分点」「外分点」の計算
- 2 「方程式が表すグラフ」ってそもそも何?
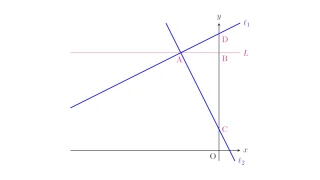
- 3 直線の傾きと平行条件・垂直条件
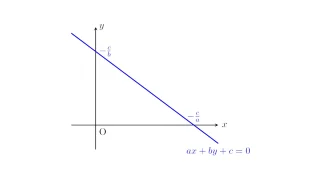
- 4 一般の直線の方程式の平行条件・垂直条件
- 5 点と直線の距離の考え方と公式を理解する
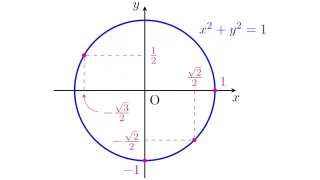
- 6 2種類の円の方程式をマスターしよう
- 7 円と直線の共有点の個数の2つの判定法
- 8 円の接線の方程式を一発で求める公式
- 9 2円の共有点を通る直線・円はこう求めよ!
Warning: Undefined array key "slug" in /home/yatamaku/yama-taku.science/public_html/wp-content/themes/cocoon-child-master/Category.php on line 472
Warning: Undefined array key "slug" in /home/yatamaku/yama-taku.science/public_html/wp-content/themes/cocoon-child-master/Category.php on line 472
Warning: Undefined array key "slug" in /home/yatamaku/yama-taku.science/public_html/wp-content/themes/cocoon-child-master/Category.php on line 472
Warning: Undefined array key "slug" in /home/yatamaku/yama-taku.science/public_html/wp-content/themes/cocoon-child-master/Category.php on line 472
Warning: Undefined array key "slug" in /home/yatamaku/yama-taku.science/public_html/wp-content/themes/cocoon-child-master/Category.php on line 472
Warning: Undefined array key "slug" in /home/yatamaku/yama-taku.science/public_html/wp-content/themes/cocoon-child-master/Category.php on line 472
Warning: Undefined array key "slug" in /home/yatamaku/yama-taku.science/public_html/wp-content/themes/cocoon-child-master/Category.php on line 472
Warning: Undefined array key "slug" in /home/yatamaku/yama-taku.science/public_html/wp-content/themes/cocoon-child-master/Category.php on line 472
Warning: Undefined array key "slug" in /home/yatamaku/yama-taku.science/public_html/wp-content/themes/cocoon-child-master/Category.php on line 472