前回の記事で説明した$xy$平面上の円の方程式について説明しました.
そこで,それまでに説明してきた$xy$平面上の直線と併せて,この記事では$xy$平面上の円と直線の関係について説明します.
円と直線の位置関係には
- 直線と円がちょうど2つ共有点をもつ
- 直線と円がちょうど1つ共有点をもつ(接する)
- 直線と円が共有点をもたない
の3種類があり,$xy$平面上の直線と円がこれらいずれになるのかを判定するには判別式または点と直線の距離を用いるのがよくある方法です.
この記事では
- 判別式による直線と円の位置関係の判定法
- 点と直線の距離による直線と円の位置関係の判定法
を順に説明します.
「図形と方程式」の一連の記事
判別式による判定法
まずは判別式の復習をしておきましょう.
2次方程式$ax^2+bx+c=0\dots(*)$に対して,$D=b^2-4ac$とすると次が成り立つ.
- $D>0\iff$方程式$(*)$が実数解をちょうど2個もつ
- $D=0\iff$方程式$(*)$が実数解をちょうど1個もつ
- $D<0\iff$方程式$(*)$が実数解をもたない
この$D=b^2-4ac$を2次方程式$ax^2+bx+c=0$ (2次式$ax^2+bx+c$)の判別式というのでした.

$xy$平面上の
- 原点中心,半径$r$の円$C$の方程式$x^2+y^2=r^2$
- 直線$\ell$の方程式$y=ax+b$
を考えます.
円$C$と直線$\ell$の共有点$(x,y)$は$x^2+y^2=r^2$と$y=ax+b$の両方を同時にみたすので,共有点は連立方程式
を解くことで得られます.$y$を消去すると,$x$の2次方程式
ができ,この2次方程式の解を$y=ax+b$に代入すると,$y$座標が求まり,この点は$x^2+y^2=r^2$をみたすことも分かります.
$x$の2次方程式の解の個数は判別式を用いて考えられることに注意すると,次が成り立つことが分かります.
[円と直線の位置関係1] 円$C:x^2+y^2=r^2$,直線$\ell:y=ax+b$について,この2式から$y$を消去してできる2次方程式の判別式を$D$とすると次が成り立つ.
- $D>0\iff$直線と円がちょうど2つ共有点をもつ
- $D=0\iff$直線と円がちょうど1つ共有点をもつ(接する)
- $D<0\iff$直線と円が共有点をもたない
単に円と直線の共有点の個数を求めるだけであれば判別式を用いれば十分ですが,実際に共有点の座標を求めるなら,具体的に方程式を解く必要があることに注意してください.
具体例1
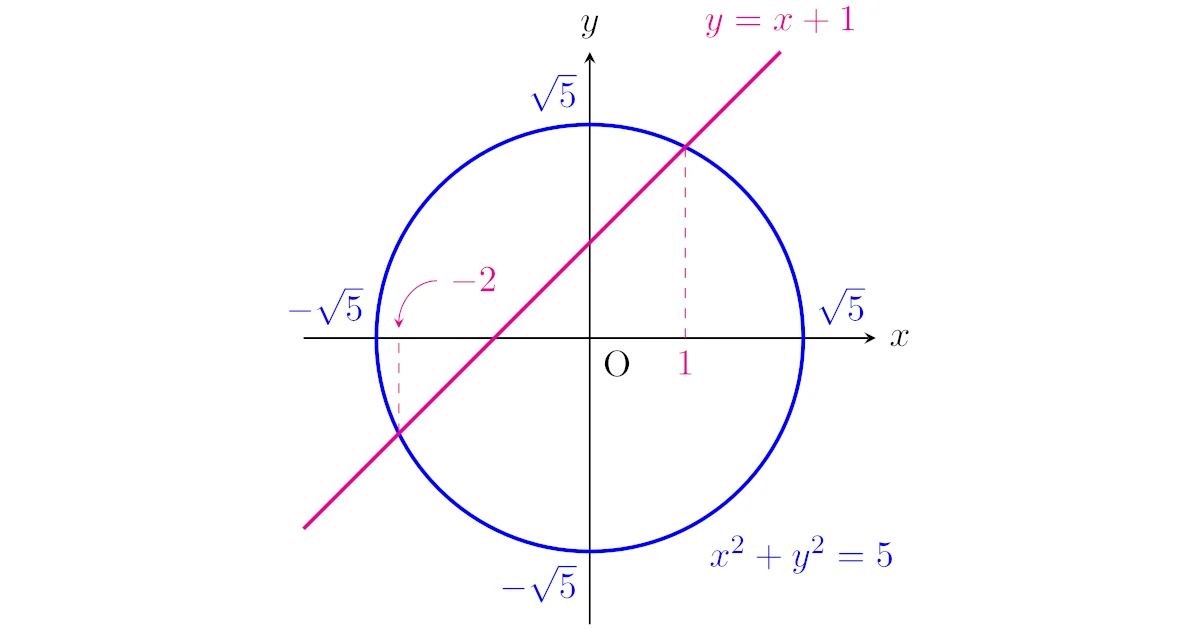
$xy$平面上の円$x^2+y^2=5$と直線$y=x+1$の共有点は何個存在するか.また,共有点が存在するとき,その共有点を全て求めよ.
共有点$(x,y)$は$x^2+y^2=5$と$y=x+1$の両方を同時にみたすから,連立方程式
の解が共有点である.$y$を消去して,
である.変形すると$(x+2)(x-1)=0$なので,共有点の$x$座標は$x=1,-2$である.
$x=1,-2$のそれぞれに対応する$y$座標は$x=2,-1$だから,共有点は$(1,2)$, $(-2,-1)$の2個存在する.
具体例2
$xy$平面上の円$x^2+y^2=2$と直線$y=x-2$の共有点は何個存在するか.また,共有点が存在するとき,その共有点を全て求めよ.
共有点$(x,y)$は$x^2+y^2=2$と$y=x-2$の両方を同時にみたすから,連立方程式
の解が共有点である.$y$を消去して,
である.変形すると$(x-1)^2=0$なので,共有点の$x$座標は$x=1$である.
$x=1$に対応する$y$座標は$-1$だから,共有点は$(1,-1)$の1個存在する.
具体例3
$xy$平面上の円$x^2+y^2=3$と直線$y=x+5$の共有点は何個存在するか.また,共有点が存在するとき,その共有点を全て求めよ.
共有点$(x,y)$は$x^2+y^2=3$と$y=x+5$の両方を同時にみたすから,連立方程式
の解が共有点である.$y$を消去して,
である.変形すると$x^2+5x+11=0$であり,この判別式は
なので,共有点は存在しない.
具体例1と具体例2では共有点が存在するため実際に2次方程式を解いていますが,具体例3では共有点が存在しないので判別式で共有点がないことを示しているわけですね.
点と直線の距離による判定法
さて,いま考えた判別式による判定法では,円の方程式と直線の方程式から文字を消去して計算する必要があったので,
- 円が原点中心でなかったり
- 直線が$y=$の形でなかったり
すると,計算が面倒になりがちです.この場合には点と直線の距離を考える方法が有効です.
[円と直線の位置関係] 円$C$と直線$\ell$について,
- 円$C$の半径を$r$
- 円$C$の中心と直線$\ell$の距離を$d$
とすると次が成り立つ.
- $d<r\iff$直線と円がちょうど2つ共有点をもつ
- $d=r\iff$直線と円がちょうど1つ共有点をもつ(接する)
- $d>r\iff$直線と円が共有点をもたない
これらはそれぞれ以下の図を考えれば当たり前ですね.
中心との距離を求める際には点と直線の距離が使えますね.
[点と直線の距離] 点$(p,q)$と直線$ax+by+c=0$の距離$d$は次で表される:
なお,点と直線の距離について,詳しくは前々回の記事を参照してください.
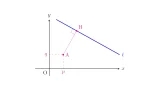
点と直線の距離の考え方と公式を理解する
具体例1
$xy$平面上の円$x^2+(y+1)^2=1$と直線$x-3y+2=0$の共有点は何個存在するか.
円の中心$(0,-1)$と直線$x-3y+1=0$との距離は
である.これは円の半径$1$より小さいので,直線と円の共有点はちょうど2個存在する.
具体例2
$xy$平面上の円$(x-4)^2+(y+3)^2=25$と直線$3x-4y+1=0$の共有点は何個存在するか.
円の中心$(4,-3)$と直線$3x-4y+1=0$との距離は,
である.これは円の半径$5$に等しいので,直線と円の共有点はちょうど1個存在する.
具体例3
$xy$平面上の円$(x-1)^2+(y+3)^2=3$と直線$x-2y+3=0$の共有点は何個存在するか.
円の中心$(1,-3)$と直線$x-2y+3=0$との距離は,
である.これは円の半径$\sqrt{3}$より大きいので,直線と円の共有点は存在しない.
点と直線の距離による判定法の計算は判別式による判定法よりもずっと楽ですが,
- この方法では共有点の座標を求めることができない
- 中心と半径が分かっていないと使えない
という2つがこの方法の欠点ですね.
コメント