２次方程式の判別式Dの考え方｜実数解の個数と虚数解の存在

次の問題はどのようにすれば解けるでしょうか？

次の２次方程式は実数解を何個もつか．

$x^2-2x-3=0$
$x^2-3x+3=0$

１つ目の２次方程式$x^2-2x-3=0$は

$\begin{align*}x^2-2x-3=0 &\iff(x-3)(x+1)=0 \\&\iff x=3,-1\end{align*}$

と因数分解から具体的に解けて実数解を２個もつことが分かります．一方，$x^2-3x+3=0$の左辺は平方完成により

$\begin{align*}x^2-3x+3 =\bra{x-\frac{3}{2}}^2+\frac{3}{4} >0\end{align*}$

となるので，$x^2-3x+3=0$は実数解を持ち得ないことが分かります．

実は，具体的に解いたり平方完成しなくても，２次方程式の実数解の個数は判別式というものを用いることで求めることができます．

また，２次方程式が実数解をもたない場合には虚数解というものを考えることができます．

この記事では，

２次方程式の判別式
虚数解

について説明します．

「多項式」の一連の記事

２次方程式の判別式
２次方程式の虚数解
1. 虚数の定義
2. ２次方程式の虚数解

２次方程式の判別式

まずは２次方程式の実数解の個数が分かる判別式について説明します．

２次方程式の解の公式と実数解の個数

まずは２次方程式の解の公式を思い出しましょう．

$a$, $b$, $c$を実数とする．２次方程式$ax^2+bx+c=0$の解は

$\begin{align*}x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\end{align*}$

と表せる．

実数解の個数を考える上で重要な部分は，この２次方程式の解の公式の$\pm\sqrt{b^2-4ac}$です．

一般に

$A\geqq0$のとき$\sqrt{A}$は０以上の実数
$A<0$のとき$\sqrt{A}$は実数でない

となることから，

$b^2-4ac>0$であれば実数解は$\dfrac{-b+\sqrt{b^2-4ac}}{2a}$, $\dfrac{-b-\sqrt{b^2-4ac}}{2a}$の２個
$b^2-4ac=0$であれば実数解は$\dfrac{-b}{2a}$の１個
$b^2-4ac<0$であれば$\sqrt{b^2-4ac}$は実数ではなく実数解は０個

となりますね．

つまり，２次方程式の解の公式の$\sqrt{\quad}$の中身$b^2-4ac$の正負から，実数解の個数が求められるわけですね．

判別式の定義

$a$, $b$, $c$を実数とする．２次方程式$ax^2+bx+c=0\dots(*)$に対して，

$\begin{align*}D=b^2-4ac\end{align*}$

を２次方程式$(*)$の判別式（discriminant）という．

歴史的には$D=b^2-4ac$を「２次式$ax^2+bx+c$の判別式」と言っても間違いではないようです．

さて，先ほど説明したことをまとめると次のようになりますね．

$a$, $b$, $c$を実数とする．２次方程式$ax^2+bx+c=0\dots(*)$の判別式$D$に対して，次が成り立つ．

$D>0\iff$方程式$(*)$は実数解をちょうど２個もつ
$D=0\iff$方程式$(*)$は実数解をちょうど１個もつ
$D<0\iff$方程式$(*)$は実数解をもたない

具体例１（$x^2-2x+2=0$）

$x$の２次方程式$x^2-2x+2=0$の実数解の個数を求めよ．

$x^2-2x+2=0$の判別式$D$は

$\begin{align*}D=(-2)^2-4\cdot1\cdot2=4-8=-4<0\end{align*}$

なので，実数解の個数は０個である．

具体例２（$x^2-3x+2=0$）

$x$の２次方程式$x^2-3x+2=0$の実数解の個数を求めよ．

$x^2-3x+2=0$の判別式$D$は

$\begin{align*}D=(-3)^2-4\cdot1\cdot2=9-8=1>0\end{align*}$

なので，実数解の個数は２個である．

具体例３（$-2x^2-x+1=0$）

$x$の２次方程式$-2x^2-x+1=0$の実数解の個数を求めよ．

$-2x^2-x+1=0$の判別式$D$は

$\begin{align*}D=(-1)^2-4\cdot(-2)\cdot1=1+8=9>0\end{align*}$

なので，実数解の個数は２個である．

具体例４（x^2-2\sqrt{3}x+1=0$）

$x$の２次方程式$3x^2-2\sqrt{3}x+1=0$の実数解の個数を求めよ．

$3x^2-2\sqrt{3}x+1=0$の判別式$D$は

$\begin{align*}D=(-2\sqrt{3})^2-4\cdot3\cdot1=12-12=0\end{align*}$

なので，実数解の個数は１個です．

２次方程式の虚数解

さて，２次方程式の実数解の個数を判別式で判定できるようになりましたが，実数解を持たない場合に「解を持たない」と言ってしまってよいのでしょうか？

少なくとも，$b^2-4ac<0$の場合にも形式的には

$\begin{align*}x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\end{align*}$

と表せるので，$\sqrt{A}$が$A<0$の場合にもうまくいくように考えたいところです．

虚数の定義

そこで次のような数を定めましょう．

２乗して$-1$になる数を虚数単位といい$i$で表す．

この定義から$i^2=-1$ですね．実数は２乗すると必ず０以上の実数となるので，この虚数単位$i$は実数ではない「何か」ということになります．

さて，$i$を単なる文字のように考えると，たとえば

$\begin{align*}(2i)^2=2^2i^2=4\cdot(-1)=-4\end{align*}$

ということになります．

一般に，虚数単位$i$は$i^2=-1$を満たす文字のように扱うことができ，$a+bi$（$a$, $b$は実数，$b\neq0$）で表される数を虚数と呼びます．

虚数について詳しくは数学IIIで学ぶことになりますが，以下の記事は数学IIIが不要な人にも参考になる内容なので，参照してみてください．

虚数・虚数単位って一体なに？複素数の考え方と基礎知識

実数は２乗すると０以上の実数となりますが，２乗して−１となる数を「虚数単位」といいます．虚数単位を用いると，実数解を持たない２次方程式の解を表せるなど，多くのメリットがあります．

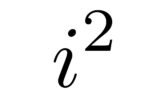
２次方程式の虚数解

虚数単位を定めると$A<0$の場合の$\sqrt{A}$も虚数単位を用いて表すことができるので，実数解を持たない２次方程式の解を虚数として表すことができます．

具体例１（$x^2+1=0$）

$x$の２次方程式$x^2+1=0$を解け．

２次方程式の解の公式より，$x^2+1=0$の解は

$\begin{align*}x=&\frac{-0\pm\sqrt{0^2-4\cdot1\cdot1}}{2\cdot1} \\=&\frac{\pm\sqrt{-4}}{2} =\frac{\pm2i}{2} =\pm i\end{align*}$

となります．

$i^2=-1$, $(-i)^2=-1$なので，パッと$x=\pm i$と答えることもできますね．

２次方程式の虚数解の具体例２（$x^2+3=0$）

$x$の次の２次方程式$x^2+3=0$を解け．

２次方程式の解の公式より，$x^2+3=0$の解は

$\begin{align*}x=&\frac{-0\pm\sqrt{0^2-4\cdot1\cdot3}}{2\cdot1} \\=&\frac{\pm\sqrt{-12}}{2} =\frac{\pm2\sqrt{3}i}{2} =\pm\sqrt{3}i\end{align*}$

となります．

$(\sqrt{3}i)^2=-3$, $(-\sqrt{3}i)^2=-3$なので，パッと$x=\pm\sqrt{3}i$と答えることもできますね．

２次方程式の虚数解の具体例３（$x^2+2x+2=0$）

$x$の次の２次方程式$x^2+2x+2=0$を解け．

２次方程式の解の公式より，$x^2+2x+2=0$の解は

$\begin{align*}x=&\frac{-2\pm\sqrt{2^2-4\cdot1\cdot2}}{2\cdot1} \\=&\frac{-2\pm\sqrt{-4}}{2} =\frac{-2\pm2i}{2} =-1\pm i\end{align*}$

となります．

平方完成により

$\begin{align*}x^2+2x+2=0 &\iff(x+1)^2=-1 \\&\iff x+1=\pm i \\&\iff x=-1\pm i\end{align*}$

と求めても構いません．