２次関数の最小値・最大値は平方完成が鉄板！

$xy$平面において，中学校では１次関数$y=ax+b$のグラフは直線であり，２次関数$y=ax^2$のグラフは原点$(0,0)$を頂点とする放物線になるのでした．

実は２次関数はこの形だけではなく，一般に

$\begin{align*}y=ax^2+bx+c\quad(a\neq0)\end{align*}$

の形の関数も２次関数といいます．

この形の２次関数もグラフは放物線となりますが，中学のときと違うのは放物線の頂点が原点ではないところです．

よって，放物線の頂点を求める方法が欲しいわけですが，そのためには平方完成というものを用いることになります．

この記事では，

平方完成
２次関数のグラフ
２次関数の最大値・最小値

を順に説明します．

「多項式」の一連の記事

平方完成
２次関数のグラフと最大値・最小値
1. ２次関数のグラフ（放物線）
2. ２次式の最大値と最小値

平方完成

まずは平方完成を解説します．

ポイントとなる因数分解公式

まずは前々回の記事で説明した次の２乗の因数分解公式を思い出しておきましょう．

$\begin{align*}&x^2+2ax+a^2=(x+a)^2,\\&x^2-2ax+a^2=(x-a)^2\end{align*}$

$x^2+2ax+a^2=(x+a)^2$で$a$を$-a$に置き換えれば$x^2-2ax+a^2=(x-a)^2$が得られるので，これらは本質的に同じ公式です．

多項式１
「展開」「因数分解」の基本の４公式

多項式を扱う上で「展開」と「因数分解」は避けては通れません．特に２次式の展開と因数分解にはそれぞれ４つの基本公式があり，これらは当たり前のように扱えるようになっておくことが大切です．

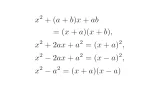
これらの公式で重要なことは，１次の係数$\pm2a$の$\frac{1}{2}$倍$\bra{\pm2a\times\frac{1}{2}}^2$が定数項$a^2$に等しくなっているという点です：

$\begin{align*}\bra{\pm2a\times\frac{1}{2}}^2=(\pm a)^2=a^2\end{align*}$

このことを用いて２次式を変形するのが平方完成です．

平方完成の仕組み

平方完成とは次のような式変形のことを言います．

２次式$ax^2+bx+c$ ($a\neq0$)を

$\begin{align*}a(x+p)^2+q\end{align*}$

の形の式に変形することを平方完成という．

たとえば，次のように平方完成ができます．

$\begin{align*} &x^2+2x=(x+1)^2-1, \\&x^2+6x+1=(x+3)^2-8, \\&3x^2-6x+1=3(x-1)^2-2, \\&2x^2-2x+1=2\bra{x-\frac{1}{2}}^2+\frac{1}{2} \end{align*}$

実は，一般に２次式$x^2+bx+c$ ($a\neq0$)の平方完成は次の手順を踏むことでできます．

$b$の$\frac{1}{2}$倍の$2$乗$\bra{b\times\frac{1}{2}}^2=\frac{b^2}{4}$を足し引きする：$x^2+bx+\frac{b^2}{4}-\frac{b^2}{4}+c$
$x^2+bx+\frac{b^2}{4}$を$(\quad)$でひとまとめにする：$\bra{x^2+bx+\frac{b^2}{4}}-\frac{b^2}{4}+c$
$(\quad)$の部分に２乗の因数分解公式を用いる：$\bra{x+\frac{b}{2}}-\frac{b^2}{4}+c$

一般的に書くと難しく感じるかもしれませんが，以下で具体的にやってみましょう．実際にやってみれば，それほど難しいものではないことが分かって頂けると思います

例１

２次式$x^2+2x$を平方完成せよ．

$x^2+2x$の１次の係数$2$の$\frac{1}{2}$倍の$2$乗は$\bra{2\times\frac{1}{2}}^2=1$なので，この$1$を足し引きして

$\begin{align*}x^2+2x=&x^2+2x+1-1\\=&(x^2+2x+1)-1\end{align*}$

とします．このとき$x^2+2x+1$に２乗の因数分解公式が使えて

$\begin{align*}x^2+2x=(x+1)^2-1\end{align*}$

となります．

例２

２次式$x^2+6x+1$を平方完成せよ．

$x^2+6x+1$の１次の係数$6$の$\frac{1}{2}$倍の$2$乗は$\bra{6\times\frac{1}{2}}^2=9$なので，この$9$を足し引きして

$\begin{align*}x^2+6x+1=&x^2+6x+9-9+1\\=&(x^2+6x+9)-9+1\end{align*}$

とします．このとき$x^2+6x+9$に２乗の因数分解公式が使えて

$\begin{align*}x^2+2x=(x+3)^2-8\end{align*}$

となります．

例３

２次式$3x^2-6x+1$を平方完成せよ．

２次の係数が$3$なので，一旦２次の係数$3$で１次と２次をくくると平方完成ができます．

$3x^2-6x+1$の２次の係数$3$で１次と２次をくくって

$\begin{align*}3x^2-6x+1=3(x^2-2x)+1\end{align*}$

です．$(\quad)$の中の１次の係数$-2$の$\frac{1}{2}$倍の$2$乗は$\bra{-2\times\frac{1}{2}}^2=1$なので，この$1$を$(\quad)$の中で足し引きして

$\begin{align*}3x^2-6x+1=&3(x^2-2x+1-1)+1\\=&3\{(x^2-2x+1)-1\}+1\end{align*}$

とします．このとき$x^2-2x+1$に２乗の因数分解公式が使えて

$\begin{align*}3x^2-6x+1=&3\{(x-1)^2-1\}+1\\=&3(x-1)^2-3+1\\=&3(x-1)^2-2\end{align*}$

となります．

例４

２次式$2x^2-2x+1$を平方完成せよ．

この問題も２次の係数が$2$なので，一旦この$2$で１次と２次をくくります．

$2x^2-2x+1$の２次の係数$2$で１次と２次をくくって

$\begin{align*}2x^2-2x+1=2(x^2-x)+1\end{align*}$

です．$(\quad)$の中の１次の係数$-1$の$\frac{1}{2}$倍の$2$乗は$\bra{-1\times\frac{1}{2}}^2=\frac{1}{4}$なので，この$\frac{1}{4}$を$(\quad)$の中で足し引きして

$\begin{align*}2x^2-2x+1=&2\bra{x^2-x+\frac{1}{4}-\frac{1}{4}}+1\\=&2\brb{\bra{x^2-x+\frac{1}{4}}-\frac{1}{4}}+1\end{align*}$

とします．このとき$x^2-x+\frac{1}{4}$に２乗の因数分解公式が使えて

$\begin{align*}2x^2-2x+1=&2\brb{\bra{x-\frac{1}{2}}^2-\frac{1}{4}}+1\\=&2\bra{x-\frac{1}{2}}^2-\frac{1}{2}+1\\=&2\bra{x-\frac{1}{2}}^2+\frac{1}{2}\end{align*}$