因数定理・剰余の定理は当たり前！考え方と具体例から理解する

３次以上の多項式の因数分解を考えるとき，以前の記事で説明したような因数分解公式が使えれば良いのですが，公式を適用できないこともよくあります．

このように公式が使えない場合には因数定理を用いて因数分解を考えるのが定石です．

因数定理という名前を聞くと難しそうに感じてしまうかも知れませんが，実は因数定理は難しいどころかほとんど当たり前と言ってよいような定理です．

また，因数定理の兄弟のような定理として剰余の定理があります．

剰余の定理は「多項式$f(x)$を１次式$x-a$で割ったときの余り」がすぐに求められる定理で，やはり剰余の定理も分かってしまえばほとんど当たり前の定理です．

この記事では

因数定理の考え方と具体例
剰余の定理の考え方と具体例

を具体例とともに順に説明します．

「多項式」の一連の記事

因数定理
1. 因数定理の内容と証明
2. 因数定理の具体例
剰余の定理
1. 剰余の定理の内容と証明
2. 剰余の定理の具体例
因数定理と剰余の定理の関係
1. 因数定理を用いた剰余の定理の証明
2. 剰余の定理を用いた因数定理の証明

因数定理

たとえば，多項式$f(x)$が因数分解できて

$\begin{align*}f(x)=(x-1)(x^2+x+1)\end{align*}$

となったとすると，$x=1$で$x-1=0$となるので$f(1)=0$ですね．このことを一般化して次が成り立つことが分かりますね．

[事実１]　多項式$f(x)$と定数$a$に対して，多項式$g(x)$を用いて$f(x)=(x-a)g(x)$と表せるとき，$f(a)=0$が成り立つ．

「多項式$f(x)$が$x-a$を因数にもつとき$f(a)=0$となる」と言っても同じことですね．

それでは，次にこの逆を考えましょう．つまり，もし多項式$f(x)$が$f(a)=0$を満たせば，$f(x)$は$x-a$を因数にもつでしょうか？

言い換えれば，多項式$f(x)$が$f(a)=0$を満たすにもかかわらず，$f(x)=(x-a)g(x)$と表せないことはあるでしょうか？

結論から言えば，多項式$f(x)$が$f(a)=0$を満たすなら必ず$f(x)=(x-a)g(x)$と表せることが証明でき，この事実を因数定理といいます．

因数定理の内容と証明

[因数定理]　多項式$f(x)$と定数$a$に対して，$f(a)=0$が成り立つとき$f(x)$は$x-a$を因数にもつ．

確かにもし$f(x)=(x-a)g(x)+b$となる$0$でない実数$b$が存在すれば，$f(a)=0$となることはありませんから成り立つことは当たり前に思えますね？

実際，因数定理は次のように証明できます．

一般に多項式を１次式で割った余りは定数なので，$f(x)$を$x-a$で割った商を$g(x)$，余りを$b$とする．すなわち，

$\begin{align*}f(x)=(x-a)g(x)+b\end{align*}$

とする．このとき，仮定$f(a)=0$と

$\begin{align*}f(a)=(a-a)g(a)+b=b\end{align*}$

を併せて$b=0$を得る．

よって，$f(x)=(x-a)g(x)$が成り立つ．すなわち，$f(x)$は$x-a$を因数にもつ．

なお，多項式の割り算については前回の記事を参照してください．

多項式７
多項式の割り算の商・余りを考え方から理解する

多項式の割り算において，整数の割り算と同様の考え方で商と余りが定義されます．この記事では多項式の割り算の考え方から説明し，具体例から商と余りの求め方を解説します．

因数定理の具体例

３次以上の多項式を因数分解するときは，最初に公式で因数分解できないかを考えます．

具体例１

$x^3-6x^2+11x-6$を因数分解せよ．

実際に$x$にいろいろ数を代入してみて，$0$となるような数$a$を見つけることができれば，因数定理から$x-a$を因数に持つことが分かります．

この場合は$x=1$で$0$となることが分かるので，因数定理から$x-1$を因数に持つことが分かります．

この３次式に$x=1$を代入すると

$\begin{align*}1^3-6\cdot1^2+11\cdot1-6=1-6+11-6=0\end{align*}$

となるから，因数定理より$x^3-6x^2+11x-6$は$x-1$を因数にもつ．

$x^3+4x^2-5$を$x-1$で割ると

$\begin{align*}\begin{matrix} &&x^2&-5x&-6&\\ \cline{2-6} x-1&\!\!\!\big)&x^3&-6x^2&11x&-6\\ &&x^3&-x^2&&\\ \cline{2-6} &&&-5x^2&11x&-6\\ &&&-5x^2&5x&\\ \cline{2-6} &&&&6x&-6\\ &&&&6x&-6\\ \cline{2-6} &&&&&0 \end{matrix}\end{align*}$

なので，商は$x^2-5x-6$，余りは$0$である．すなわち，

$\begin{align*}x^3-6x^2+11x-6=(x^2-5x-6)(x-1)\end{align*}$

が成り立つ．さらに，２次式$x^2-5x-6$は

$\begin{align*}x^2-5x-6=(x-3)(x-2)\end{align*}$

と因数分解できるから，以上をまとめて

$\begin{align*}x^3-6x^2+11x-6=(x-3)(x-2)(x-1)\end{align*}$

を得る．

因数定理から$x^3+4x^2-5$は$x-1$を因数にもつことが既に分かっているので，$x^3+4x^2-5$を$x-1$で割ったときの余りが$0$なのは当たり前ですね．

具体例２

次の問題も考え方は例１と全く同じで，実際に$x$に数を代入して$0$になるものを見つけましょう．

$3x^3-7x^2-7x+3$を因数分解せよ．

この３次式に$x=-1$を代入すると，

$\begin{align*}3\cdot(-1)^3-7\cdot(-1)^2-7\cdot(-1)+3=-3-7+7+3=0\end{align*}$

となるから，因数定理より$3x^3-7x^2-7x+3$は$x+1$を因数にもつ．

$3x^3-7x^2-7x+3$を$x+1$で割ると

$\begin{align*}\begin{matrix} &&3x^2&-10x&3&\\ \cline{2-6} x+1&\!\!\!\big)&3x^3&-7x^2&-7x&3\\ &&3x^3&3x^2&&\\ \cline{2-6} &&&-10x^2&-7x&3\\ &&&-10x^2&-10x&\\ \cline{2-6} &&&&3x&3\\ &&&&3x&3\\ \cline{2-6} &&&&&0 \end{matrix}\end{align*}$

なので，商は$3x^2-10x+3$，余りは$0$である．すなわち，

$\begin{align*}3x^3-7x^2-7x+3=(3x^2-10x+3)(x+1)\end{align*}$

が成り立つ．さらに，２次式$3x^2-10x+3$は

$\begin{align*}3x^2-10x+3=(3x-1)(x-3)\end{align*}$

と因数分解できるから，以上をまとめて

$\begin{align*}3x^3-7x^2-7x+3=(3x-1)(x-3)(x+1)\end{align*}$

を得る．

剰余の定理

因数定理は次の[事実１]の逆なのでした．

[事実１(再掲)]　多項式$f(x)$と定数$a$に対して，多項式$g(x)$を用いて$f(x)=(x-a)g(x)$と表せるとき，$f(a)=0$が成り立つ．

この[事実１]と同じように，次の[事実２]も当たり前ですね．

[事実２]　多項式$f(x)$と定数$a$, $b$に対して，多項式$g(x)$を用いて$f(x)=(x-a)g(x)+b$と表せるとき，$f(a)=b$が成り立つ．

「多項式$f(x)$を$x-a$で割った余りが$b$のとき$f(a)=b$となる」と言っても同じことですね．

剰余の定理の内容と証明

[事実１]の逆は正しく因数定理と言ったように，[事実２]の逆も正しく，これが剰余の定理です．

[剰余の定理]　多項式$f(x)$と定数$a$, $b$に対して，$f(a)=b$が成り立つとき$f(x)$を$x-a$で割った余りは$b$である．

剰余の定理は「$f(a)=c$となるとき，$f(x)=(x-a)g(x)+c$となる多項式$g(x)$が存在する」とも言い換えられますね．

一般に多項式を１次式で割った余りは定数なので，$f(x)$を$x-a$で割った商を$g(x)$，余りを$c$とする．すなわち，

$\begin{align*}f(x)=(x-a)g(x)+c\end{align*}$

とする．このとき，仮定$f(a)=b$と

$\begin{align*}f(a)=(a-a)g(a)+c=c\end{align*}$

を併せて$b=c$を得る．

よって，$f(x)=(x-a)g(x)+b$が成り立つ．すなわち，$f(x)$を$x-a$で割った余りは$b$である．

剰余の定理の具体例

多項式を１次式で割ったときの余りは，剰余の定理を用いれば一発で分かります．

具体例１

$x^3-6x^2+4x+3$を$x-5$で割った余りを求めよ．

剰余の定理より，求める余りは$x^3-6x^2+4x+3$に$x=5$を代入したものに等しく

$\begin{align*}5^3-6\cdot5^2+4\cdot5+3=125-150+20+3=-2\end{align*}$

である．

剰余の定理を使わなくても，実際に$x^3-6x^2-4x+3$を$x-5$で割って

$\begin{align*}x^3-6x^2+4x+3=(x-5)(x^2-x-1)-2\end{align*}$

としても余りが$-2$であることは分かりますが，剰余の定理を使う方がよっぽど楽ですね．

具体例２

次の問題も「多項式を１次式で割った余り」なので，例１と同様に解けますね．

$3x^4-4x^2-2x+7$を$x-2$で割った余りを求めよ．

剰余の定理より，求める余りは$3x^4-4x^2-2x+7$に$x=2$を代入したものに等しく

$\begin{align*}3\cdot2^4-4\cdot2^2-2\cdot2+7=48-16-4+7=35\end{align*}$

である．

因数定理と剰余の定理の関係

この記事では因数定理と剰余の定理を別々に証明しました．しかし，実は

因数定理を用いて剰余の定理を示す
剰余の定理を用いて因数定理を示す

ということができます．

つまり，剰余の定理と因数定理は本質的に同じ定理ということになります．

因数定理を用いた剰余の定理の証明

剰余の定理

[剰余の定理(再掲)]　多項式$f(x)$と定数$a$, $b$に対して，$f(a)=b$が成り立つとき$f(x)$を$x-a$で割った余りは$b$である．

多項式$f(x)-f(a)$に$x=a$を代入すると$0$となるから因数定理より，多項式$g(x)$を用いて$f(x)-f(a)=(x-a)g(x)$と表せる．

よって，$f(a)$を移項して$f(x)=(x-a)g(x)+f(a)$となるから，$f(x)$を$x-a$で割った余りは$f(a)$である．

$f(x)-f(a)$が$x=a$で$0$になることから，因数定理が適用できるわけですね．

剰余の定理を用いた因数定理の証明

[因数定理(再掲)]　多項式$f(x)$と定数$a$に対して，$f(a)=0$が成り立つとき$f(x)$は$x-a$を因数にもつ．

剰余の定理より多項式$f(x)$は多項式$g(x)$を用いて$f(x)=(x-a)g(x)+f(a)$と表せる．

$f(a)=0$が成り立つことから$f(x)=(x-a)g(x)$となるから，$f(x)$は$x-a$を因数にもつ．

因数定理は剰余の定理の余りが$0$の場合に相当するというわけですね．

このように，因数定理と剰余の定理は互いに密接に関わっていることが分かりますね．

多項式８
因数定理・剰余の定理は当たり前！

因数定理

因数定理の内容と証明

因数定理の具体例

具体例１

具体例２

剰余の定理

剰余の定理の内容と証明

剰余の定理の具体例

具体例１

具体例２

因数定理と剰余の定理の関係

因数定理を用いた剰余の定理の証明

剰余の定理を用いた因数定理の証明

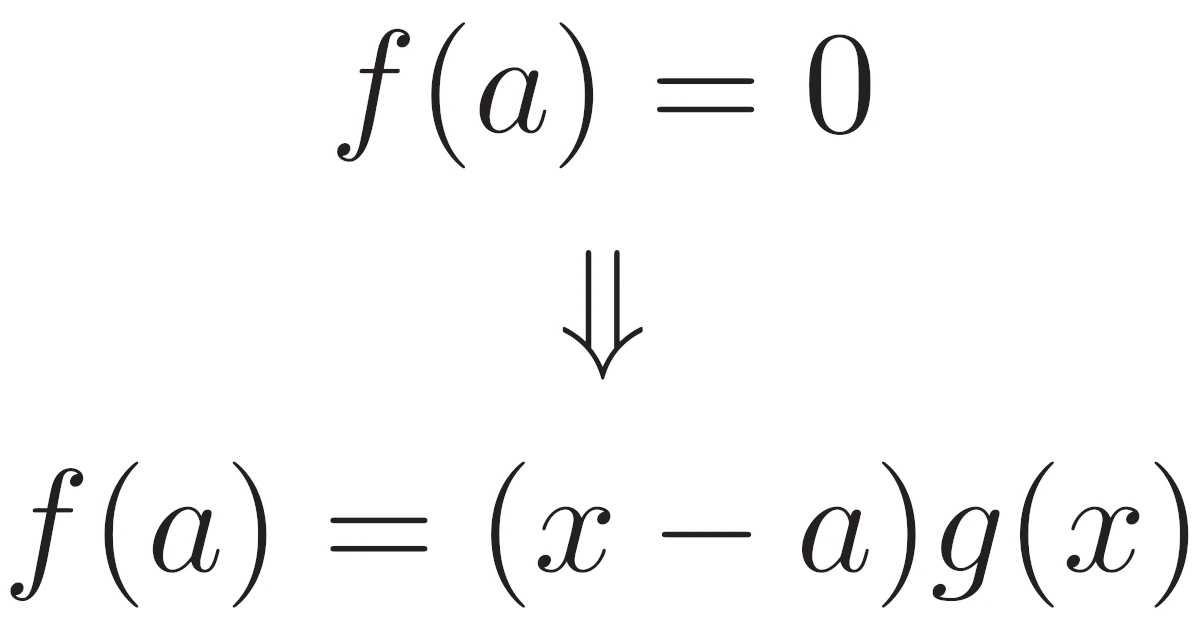
コメント