算数と数学との大きな違いの1つに,文字式を使うか使わないかということが挙げられます.
中学1年生の数学では最初に文字の計算を学び始め,特定の数字ではなく「文字」で計算することにより多くのことが分かるようになるのでした.
そのため,数学を学ぶにあたって文字の計算がきちんとできることは必須になるわけですが,その中でも展開と因数分解は数学のいたるところに現れるので,確実にできるようになっておく必要があります.
この記事では,中学の復習として
- 2次式の展開
- 2次式の因数分解
- 基本公式の図形的意味
を順に復習します.
「多項式」の一連の記事
2次式の展開
例えば,$(x+2)(x-4)$は
と計算することができますね.このように,多項式の積などの括弧$(\quad)$を外す計算を展開というのでした.
展開の基本公式
展開については次の公式が基本的なのでした.
実数$x$, $a$, $b$に対して,等式
が成り立つ.
この等式は上の例のように単純に左辺を展開して$x$でまとめれば得られますね.
展開の基本公式の具体例
いくつか具体例を見ておきましょう.
具体例1
$(x+2)(x+3)$を展開せよ.
基本公式で$a=2$, $b=3$として
と展開できる.
具体例2
$(x+2)^2$を展開せよ.
基本公式で$a=2$, $b=2$として
と展開できる.
具体例3
$(x-3)^2$を展開せよ.
基本公式で$a=-3$, $b=-3$として
と展開できる.
具体例4
$(x+5)(x-5)$を展開せよ.
基本公式で$a=5$, $b=-5$として
と展開できる.
2次式の因数分解
展開とは逆に多項式を積の形に書き直すことを因数分解というのでした.
因数分解の基本公式
展開では分配法則でただ計算するだけなので難しくはありませんが,$x^2-2x-8$を因数分解して$(x+2)(x-4)$に戻すことは少し難しいのでした.
そこで,先ほどの展開公式を因数分解公式として左辺と右辺を入れ替えて眺めてみましょう.
実数$x$, $a$, $b$に対して,等式
が成り立つ.
つまり
- $ab$が定数項
- $a+b$が1次の係数
と表せるような$a$, $b$を見つけてくれば,$(x+a)(x+b)$と因数分解できるわけですね.
展開公式からすぐに導出できますが,標語的にも「積が定数,和が1次」と当たり前にしておきましょう.
因数分解の基本公式の具体例
いくつか具体例を見ておきましょう.
具体例1
$x^2-x-20$を展開せよ.
$ab=-20$, $a+b=-1$となる$a$, $b$として,$a=-5$, $b=4$が見つかるので基本公式より
と因数分解できる.
具体例2
$x^2+18x+81$を展開せよ.
$ab=81$, $a+b=18$となる$a$, $b$として,$a=9$, $b=9$が見つかるので基本公式より
と因数分解できる.
具体例3
$x^2-12x+36$を展開せよ.
$ab=36$, $a+b=-12$となる$a$, $b$として,$a=-6$, $b=-6$が見つかるので基本公式より
と因数分解できる.
具体例4
$x^2-49$を展開せよ.
$ab=-49$, $a+b=0$となる$a$, $b$として,$a=7$, $b=-7$が見つかるので基本公式より
と因数分解できる.
因数分解の補足
いまみた因数分解の問題では$a$, $b$が簡単に見つかりましたが,一般には簡単に見つかるとは限りません.
例えば,$x^2-2x-2$を因数分解すると
となりますが,$ab=-2$, $a+b=-2$から$a=-1+\sqrt{3}$, $b=-1-\sqrt{3}$を見つけるのは難しいですね.
このような場合にどうすれば因数分解できるかについては,のちの記事で説明しています.
展開・因数分解の4公式
上では基本公式
のみを考えました.
公式
この公式は万能なのですが,$(x+a)^2$, $(x-a)^2$, $(x+a)(x-a)$の形もよく出てくるので,次の4つで併せて当たり前にしておきましょう.
実数$x$, $a$, $b$に対して,次の等式が成り立つ.
2つ目〜4つ目の公式はいずれも1つ目の公式の特別な場合で,右辺を展開すれば同様に証明できますね.
具体例
2つ目〜4つ目の公式を用いて,先ほどの因数分解の具体例2〜具体例2をもう一度解いておきましょう.
次を展開せよ.
- $x^2+18x+81$
- $x^2-12x+36$
- $x^2-49$
- 公式$x^2+2ax+a^2=(x+a)^2$で$a=9$として,
- 公式$x^2-2ax+a^2=(x-a)^2$で$a=-6$として,
- 公式$x^2-a^2=(x+a)(x-a)$で$a=7$として,
当然ですが,慣れてくればパッと答えを出せるようになります.
展開・因数分解の基本公式の図形的意味
$x>0$, $a$, $b>0$なら,次の図から等式
は直感的に理解することもできます.
この長方形の面積は
- 4つの部分の面積の和
- 縦$(x+a)$・横$(x+b)$の長方形の面積
と2通りで考えることができ,それぞれ
- $x^2+ax+bx+ab(=x^2+(a+b)x+ab)$
- $(x+a)(x+b)$
なので,等式$x^2+(a+b)x+ab=(x+a)(x+b)$が従いますね.
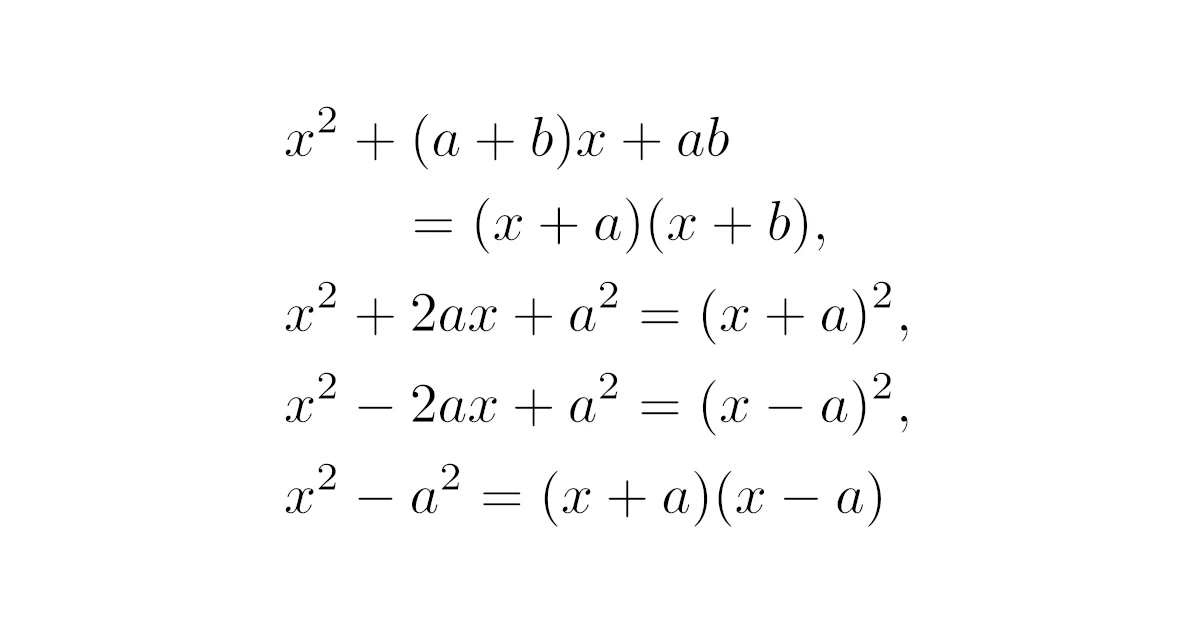
コメント