微分可能な関数$f(x)$に対しては導関数$f'(x)$を考えることにより,$xy$平面上のグラフ$y=f(x)$の接線の傾きを考えることができるのでした.
導関数$f'(x)$を用いると
- $f'(x)>0$ → $x$での接線の傾きが正 → $x$で$f$は増加
- $f'(x)<0$ → $x$での接線の傾きが負 → $x$で$f$は減少
と関数$f(x)$の増減を考えることもできますね.
このように,微分法は関数の増減を調べるために非常に便利ですが,関数はいつでも微分可能であるとは限りません.
微分可能でないことを微分不可能と言いますが,高校数学では微分不可能であるような関数を扱うことは多くありません.
とはいえ,数学IIIでは微分の考え方をある程度扱うため実際の入試でも問われることもあり,微分不可能であるような具体例もきちんと知っておくことも大切です.
この記事では
- 微分可能性
- 微分可能性と連続性の関係
- 微分不可能な関数の具体例
を順に説明します.
この記事と併せて,例えば次の記事も参照してみてください.
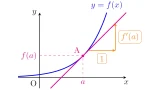
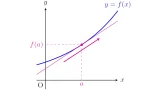
y=f(x)のグラフの描き方は4ステップでOK
微分可能性
最初に微分可能性の定義を確認しておきましょう.
関数の極限
微分可能であることの定義には極限が必要なので,まずは極限を復習しておきましょう.
関数$f(x)$に対して,$x$が$a$と異なる値を取りながら$a$に限りなく近づくとき,$f(x)$がある一定の値$\alpha$に限りなく近付くならば,このことを
または
$x \to a$のとき$f(x)\to\alpha$
と表し,「$x\to a$のとき$f(x)$は$\alpha$に収束する」といい,この$\alpha$を「$x\to a$のときの$f(x)$の極限値」という.
微分不可能な関数を考える際には,極限に関する次の定理が重要です.
関数$f(x)$と実数$a$に対して,極限$\lim\limits_{x\to a}f(x)$が存在するためには
- $x>a$で$x\to a$とする右極限$\lim\limits_{x\to a+0}f(x)$
- $x<a$で$x\to a$とする左極限$\lim\limits_{x\to a-0}f(x)$
が共に存在して一致することが必要十分である.
この「右極限」と「左極限」は数学IIIの範囲ですね.
また,$a=0$のときは,右極限を$\lim\limits_{x\to +0}f(x)$,左極限を$\lim\limits_{x\to -0}f(x)$と表しますね.
要するに
- $x$を大きい方から$a$に近付けたときに$f(x)$が近付く値(右極限)
- $x$を小さい方から$a$に近付けたときに$f(x)$が近付く値(左極限)
が一致すれば$f(x)$は$x\to a$の極限をもち,この逆も成り立つというわけですね.
関数の微分可能性
関数が微分可能であるとは次のように定義されます.
関数$f(x)$と実数$a$に対して,極限
が有限の値として存在するとき,$f(x)$は$x=a$で微分可能であるという.また,微分可能でないとき,微分不可能であるという.
定義式は
で書かれることもありますが,どちらも同じ式であることについては以下の記事を参照してください.
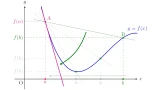
微分可能性を考えるときには
- どの関数が
- どこで
という2つの情報が重要です.
直感的には「$f(x)$が$x=a$で微分可能である」とは「グラフ$y=f(x)$は$x=a$で接線が引ける(なめらか)である」ということを表しています.
微分可能性と連続性の関係
関数$f(x)$が$a$で微分可能性であれば,$f(x)$は$a$で連続性となります.
このことを確認しておきましょう.
連続性の定義
関数$f(x)$と実数$a$に対して,$\lim\limits_{x\to a}f(x)$が存在して$f(a)$に一致するとき,$f(x)$は$x=a$で連続であるという.また,連続でないとき不連続であるという.
微分可能性と同様に,連続性を考えるときには
- どの関数が
- どこで
という2つが重要です.
直感的には「$f(x)$が$x=a$が連続である」とは「グラフ$y=f(x)$が$x=a$で繋がっている」ということを表しています.
微分可能性と連続性の関係
関数$f(x)$のグラフ$y=f(x)$が滑らかなら,もちろんグラフは繋がっているはずですから,次の定理が成り立つことは自然ですね.
関数$f(x)$と実数$a$に対して,$f(x)$が$x=a$で微分可能であれば$f(x)$は$x=a$で連続である.
逆は成り立たないことに注意してください.つまり,連続であっても微分不可能であることもありえます.
関数$f(x)$と実数$a$に対して,$f(x)$が$x=a$で微分可能であることから,極限
が有限の値として存在する.この極限値を$\alpha$とすると,
が成り立つ.以上より,$f(x)$が$x=a$で連続であることが従う.
別の書き方をすれば,極限
について,分母は$\lim\limits_{b\to a}(b-a)=0$なので,もし分子の極限が$0$でなければ$\lim\limits_{b\to a}\dfrac{f(b)-f(a)}{b-a}$が有限の値になり得ませんから,分子の極限も$0$になるしかないわけですね.
さて,微分不可能なこの定理の対偶である次の定理は,微分不可能な関数を考える際に有効なことがあります.
関数$f(x)$と実数$a$に対して,$f(x)$が$x=a$で不連続であれば,$f(x)$は$x=a$で微分不可能である.
つまり,微分可能かどうかを見る前に不連続であれば,その時点で問答無用で微分不可能であることが分かるわけですね.
微分可能性の例
それでは,いくつか具体例を考えましょう.
例1
次の関数$f(x)$は$x=0$で微分可能か.
グラフを見ると$x=0$で不連続ですから,微分不可能であることがみてとれますね.
きちんと式で処理するなら次のようになります.
右極限は
であり,左極限は
だから,右極限と左極限は一致しない.
よって,極限$\lim\limits_{x\to0}f(x)$が存在しないから$f(x)$は$x=0$で不連続なので,$f(x)$は$x=0$で微分不可能である.
例2
次の関数$f(x)$は$x=0$で微分可能か.
例1と同じくグラフを見ると$x=0$で不連続ですから,微分不可能であることがみてとれますね.
右極限は
であり,左極限は
だから,右極限と左極限は一致するので,極限$\lim\limits_{x\to0}f(x)$が存在して$0$となる.
しかし,$f(0)=1$だから,$\lim\limits_{x\to0}f(x)\neq f(0)$となって$f(x)$は$x=0$で不連続である.したがって,$f(x)$は$x=0$で微分不可能である.
右極限$\lim\limits_{x\to+0}f(x)$と$f(0)$が異なっていれば不連続となるので,
「$\lim\limits_{x\to+0}f(x)=0\neq1=f(0)$だから$f(x)$は$x=0$で不連続」
としても問題ありません.
例3
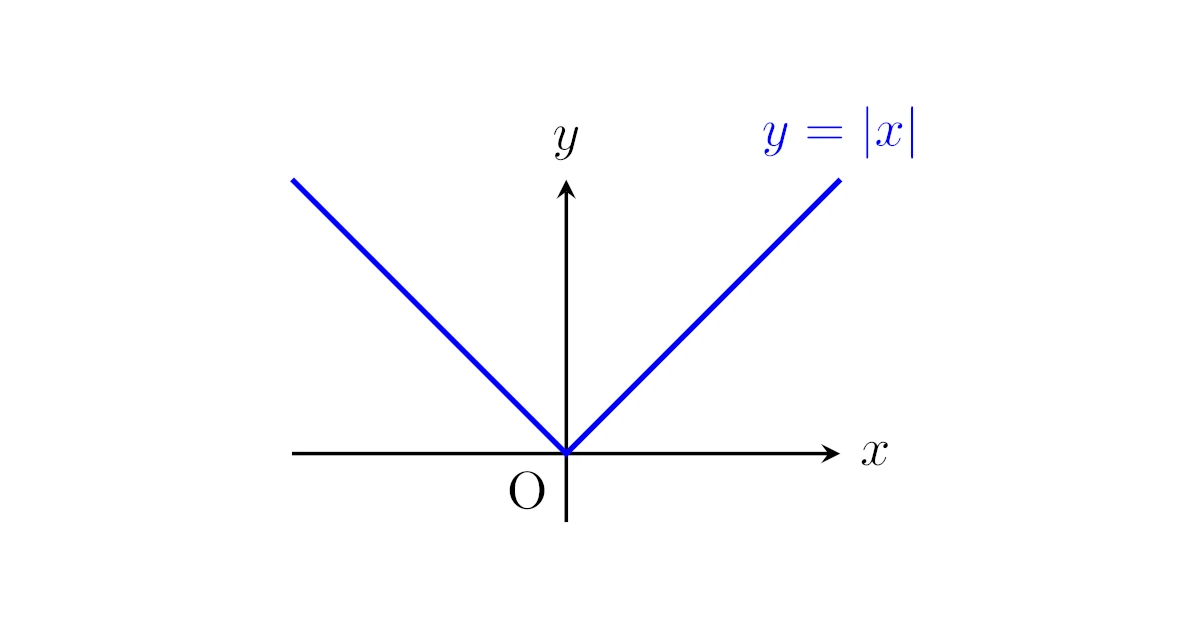
関数$f(x)=|x|$は$x=0$で微分可能か.
まず$y=f(x)$のグラフは$x=0$で「尖っている」ので微分不可能であることみてとれますが,$f(x)$は$x=0$で連続なので例1,例2のように「不連続性から微分不可能」とはできません.
よって,微分不可能であることは定義から示す必要があるわけですね.
$\dfrac{f(x)-f(0)}{x-0}$の$0$での右極限は
であり,左極限は
である.これらは一致していないから,$f(x)$は$x=0$で微分不可能である.
なお,途中の計算では
- $x>0$なら$|x|=x$
- $x<0$なら$|x|=-x$
であることを用いています.

絶対値の定義から一瞬で解ける問題
例4
次の関数$f(x)$は$x=0$で微分可能か.
$x=0$を境目にして異なる式で表されていますが,「つなぎ目」の$x=0$ではなめらかに繋がっているので微分可能となります.
$\dfrac{f(x)-f(0)}{x-0}$の$0$での右極限は
であり,左極限は
である.これらは一致しているから,$f(x)$は$x=0$で微分可能である.
コメント