絶対値をきちんとイメージから分かっていれば，例えば
- 不等式$|x-3|<5$
- 方程式$|x-2|+|x-4|=6$
などはものの数秒で答えを出すことができます．
なお，実際に予備校で教えていると
「絶対値は中身が０以上ならそのまま外す，中身が負ならマイナスをかけて外す」
と言う人は多いのですが，これは絶対値の性質であって定義ではありません．
性質が言えることはそれで素晴らしいことですが，「じゃあ，これが成り立つ理由は？」を聞くと途端に考え込んでしまう人が多いのも事実で，こうなると応用力が身に付くかは怪しくなってきます．
この記事で絶対値のイメージをしっかり理解して，自信を持って絶対値を扱えるようにしてください．
絶対値の定義
絶対値のイメージは「距離」で次のように定義されます．
[絶対値] 実数$a$に対して，$a$と原点０との距離を$a$の絶対値といい，$|a|$と表す．
絶対値はただ「原点との距離」を表しているだけなのですね．
ここで次の[事実]は当たり前ですが重要です．
実数$a$, $b$の大小関係が$b<a$であれば，$a$と$b$の距離は$a-b$である．
いわゆる「距離は『大 引く 小』」です．中学で耳にタコができるほど言われた人もいるかもしれませんね．
要するに，数直線上の２点について，右にあるものから左にあるものを引けば２点間の距離が求まるということです．
数直線を思い浮かべて，以下の例を考えてください．
- $2$と原点$0$との距離は$2-0=2$ですから，$|2|=2$です．
- $-2$と原点$0$との距離は$0-(-2)=2$ですから，$|-2|=2$です．
- $\pi$と原点$0$との距離は$\pi-0=\pi$ですから，$|\pi|=\pi$です．
- $0$と原点$0$との距離は$0-0=0$ですから，$|0|=0$です．
- $-\dfrac{2}{3}$と原点$0$との距離は$0-\bra{-\dfrac{2}{3}}=\dfrac{2}{3}$ですから，$\abs{-\dfrac{2}{3}}=\dfrac{2}{3}$です．
絶対値の定義と，いまみた事実を考えれば当たり前ですね？
帰結１
さて，次の[帰結１]も当たり前にしておきましょう．
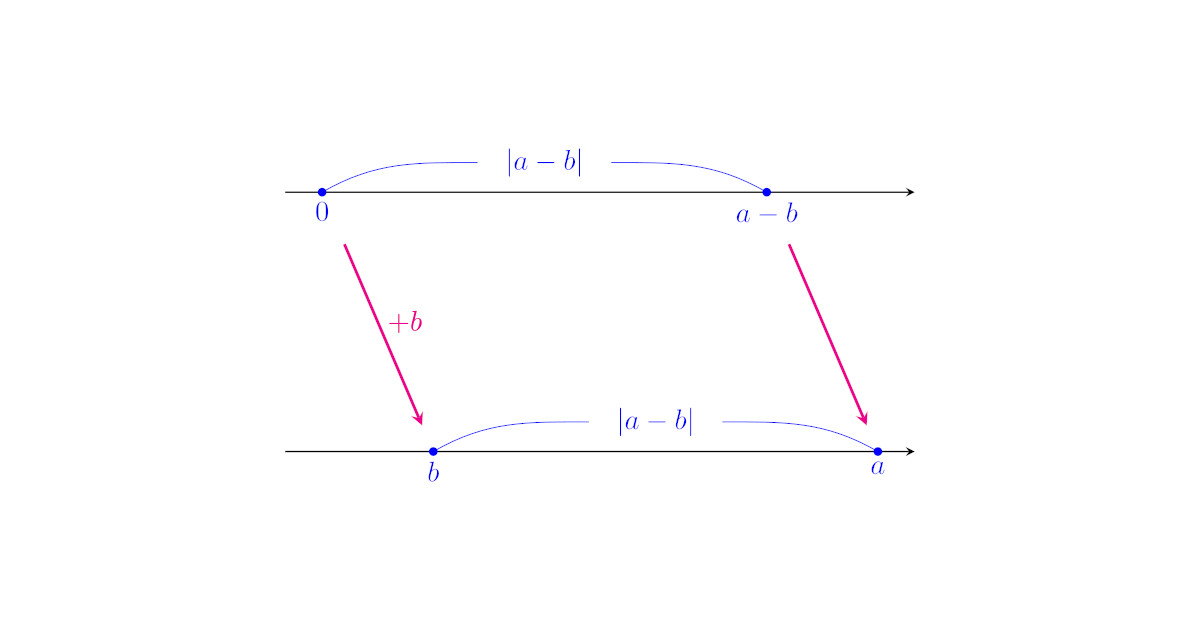
[帰結１] 実数$a$, $b$に対して，$|a-b|$は$a$と$b$の距離を表す．
$|a-b|$を定義通りに言えば「$a-b$と原点０との距離」ですね．
数直線上で$a-b$を右にちょうど$b$だけ動かした$a$と，原点０を右にちょうど$b$だけ動かした$b$との距離も，並行移動しただけですから$|a-b|$です．
したがって，$|a-b|$は$a$と$b$の距離を表すことが分かりました．
具体例
[絶対値の定義]や[帰結１]をしっかり意識していれば，次のような問題は瞬時に解けます．
次の方程式，不等式を解け．
- $|x|=2$
- $|x|<2$
- $|x-3|\leqq5$
- $|x-2|+|x-4|=8$
答えは以下の通りになります．
定義から$|x|$は$x$と原点０との距離を表す．よって，$|x|=2$は「$x$と原点０との距離が２」ということに他ならない．
したがって，$x=\pm2$を得る．
定義から$|x|$は$x$と原点０との距離を表す．よって，$|x|<2$は「$x$と原点０との距離が２より小さい」ということに他ならない．
したがって，$-2<x<2$を得る．
[帰結1]から$|x-3|$は$x$と３との距離を表す．よって，$|x-3|\leqq5$は「$x$と３との距離が５以下」ということに他ならない．
したがって，$3-5<x<3+5$，すなわち$-2<x<8$を得る．
[帰結１]から$|x-2|$は$x$と２との距離を表し，$|x-4|$は$x$と４との距離を表すから，$|x-2|+|x-4|=8$は「$x$と２との距離と，$x$と２との距離の和は８である」ということに他ならない．
２と４の距離は２なので，数直線上の２から左に３の点，数直線上の４から右に３の点は条件を満たす．
したがって，$x=-1,7$を得る．
実数$a$, $b$に対して，$|a|$は数直線上の原点０と$a$の距離を表し，$|a-b|$は数直線上の$a$と$b$の距離を表す．
帰結２
絶対値の定義のイメージができていると非常に強力な様が見てとれましたが，実際の記述答案では式変形で解くことが望まれます．
そこで，$a\ge0$のときの$|a|$と，$a<0$のときの$|a|$を分けて考えてみましょう．
[1] $a\geqq0$のとき，
なので，
となります．
[2] $a<0$のとき，
なので，
となります．
[1]は$a=3$を，[2]は$a=-3$を代入して読んでみると分かりやすいと思います．
これらをまとめたものが，絶対値の定義から分かる帰結の２つ目です．
[帰結２] 絶対値について，次が成り立つ．
これが冒頭に書いた「絶対値は中身が０以上なら……」の正体ですね．
具体例
この[帰結２]から先の問について，きちんと答案を作りましょう．
[再掲] 次の方程式，不等式を解け．
- $|x|=2$
- $|x|<2$
- $|x-3|\leqq5$
- $|x-2|+|x-4|=8$
絶対値がある場合には，絶対値の中身の正負で場合分けするのが定石です．
次の[1],[2]に分けて考える．
[1] $x\geqq0$のとき，
$|x|=x$だから，
である．これは$x\geqq0$を満たす．
[2] $x<0$のとき，
$|x|=-x$だから，
である．これは$x<0$を満たす．
[1], [2]より，解は$x=\pm2$である．
次の[1],[2]に分けて考える．
[1] $x\geqq0$のとき，
$|x|=x$だから，
である．これと$x\geqq0$を併せて$0\leqq x<2$である．
[2] $x<0$のとき，
$|x|=-x$だから，
である．これと$x<0$を併せて$-2<x<0$である．
[1], [2]より，解は$-2<x<2$である．
次の[1],[2]に分けて考える．
[1] $x\geqq3$のとき，
$x-3\geqq0$より，$|x-3|=x-3$だから，
である．これと$x\geqq3$を併せて$3\leqq x<8$である．
[2] $x<3$のとき，
$x-3<0$より，$|x-3|=-(x-3)$だから，
である．これと$x<3$を併せて$-2\leqq x<3$である．
[1], [2]より，解は$-2\leqq x\leqq8$である．
次の[1]-[3]に分けて考える．
[1] $x\geqq4$のとき，
$x-2\geqq x-4\geqq0$より，$|x-2|=x-2$かつ$|x-4|=x-4$だから，
である．これは$x\geqq4$を満たす．
[2] $4>x\geqq2$のとき，
$x-2\geqq 0>x-4$より，$|x-2|=x-2$かつ$|x-4|=-(x-4)$だから，
である．どんな$x$に対してもこの式は満たし得ないから解なし．
[3] $2>x$のとき，
$0>x-2>x-4$より，$|x-2|=-(x-2)$かつ$|x-4|=-(x-4)$だから，
である．これは$2>x$を満たす．
[1]-[3]より，解は$x=-1,7$である．
帰結１と帰結２の解法の関係
さて，以下の２つの解法を考えました．
- [絶対値]の定義と[帰結１]から数直線で考える解法
- [帰結２]から式変形で考える解法
最後に，これらは一見違った解法のように見えて，実は同じであることを見ておきましょう．
問３の場合
問3の$|x-3|\leqq5$では$x\geqq3$と$x<3$に分けて考えました．
$x\geqq3$の場合，$x-3\geqq0$より右辺$|x-3|$は$x-3$となりますが，数直線上でも
となるので，「大 引く 小」で同じく$|x-3|$は$x-3$となります．
また，$x<3$の場合も，$x-3<0$より右辺$|x-3|$は$-(x-3)=3-x$となりますが，数直線上でも
となるので，「大 引く 小」で同じく$|x-3|$は$3-x$となります．
このように，数直線上の3以上の$x$で考えるといずれの考え方でも$|x-3|=x-3$となり，3より小さい$x$で考えるといずれの考え方でも$|x-3|=3-x$となり，同じ結果が得られることになります．
問４の場合
問４の$|x-2|+|x-4|=8$では$x$が２と４の間にあるとき，「$x$と２の距離$|x-2|$」と「$x$と４の距離$|x-4|$」の和は「２と４の距離」に等しく，常に２になります．
これは「大 引く 小」から$|x-4|=4-x$かつ$|x-2|=x-2$なので両者を足すと２になるからですね．
これは式変形で考えても同様のことが起こります．
$x$が$4>x\geqq2$を満たすとき，$x-2\geqq0>x-2$だから
となって，確かにいつでも一定値２となりますね．
いずれの考え方でも，左辺$|x-2|+|x-4|$は２となるので，右辺の８になり得ず解は存在しないというわけです．
$|x-a|$を「$x$と$a$の距離」という観点で見れば，距離は「大 引く 小」で考えることになるので，$a$と$x$の左右が入れ替わる$x\geqq a$と$x<a$で場合分けすることの妥当性がみてとれる．
【次の記事：ワンポイント数学３｜根号(ルート)の基本と二重根号の外し方】
実数$a$に対して，$\sqrt{a^2}=a$は間違いだと自信を持って言えるでしょうか？実は，$\sqrt{a^2}$の根号を外すときには，絶対値が必要になります．この記事では，根号(ルート)の基本から二重根号の外し方まで解説します．