(a+b)ⁿの展開は二項定理！実は組み合わせを使えば当たり前

場合の数と確率
2017.09.16
場合の数と確率

２乗の展開公式と３乗の展開公式

    \begin{align*}&(a+b)^2=a^2+2ab+b^2, \\&(a+b)^3=a^3+3a^2b+3ab^2+b^3\end{align*}

は当たり前にしておきたい公式ですが，一般に$(a+b)^n$はどのように展開できるでしょうか？

実は組み合わせの考え方を用いると，$(a+b)^n$の展開公式である二項定理を導くことができます．

この記事では

  • 二項定理はどんな定理か？
  • 二項定理の考え方

を順に説明します．

「場合の数と確率」の一連の記事

  1. 1 樹形図が全ての基本！和の法則・積の法則
  2. 2 順列ₙPₖの考え方と公式は樹形図からイチコロ
  3. 3 実はカンタンな円順列・数珠順列の考え方
  4. 4 組み合わせₙCₖの求め方から性質まで攻略
  5. 5 重複順列の考え方・求め方をシンプルに理解する
  6. 6 重複組み合わせの問題２パターンを攻略する！
  7. 7 (a+b)ⁿの展開は二項定理！組み合わせを使って導出 (今の記事)
  8. 8 (a+b)ⁿが楽に展開できるパスカルの三角形
  9. 9 (a+b+c)ⁿの展開は多項定理！考え方と具体例

二項定理の内容と具体例

結論から言えば，$(a+b)^n$は次のように展開されます．

［二項定理］実数$a$, $b$と正の整数$n$に対して，

    \begin{align*}(a+b)^{n}=\Co{n}{0}a^{n}+\Co{n}{1}a^{n-1}b+\Co{n}{2}a^{n-2}b^2+\dots+\Co{n}{n-1}ab^{n-1}+\Co{n}{n}b^{n}\end{align*}

が成り立つ．

この展開公式を二項展開といい，このことから係数の$\Co{n}{k}$を二項係数ということもあります．

二項定理が成り立つ考え方と証明は後回しにして，まずは具体例を考えましょう．

具体例１（$(a+b)^3$の展開）

$(a+b)^{3}$を展開せよ．

二項定理を使わなくても，公式として

    \begin{align*}(a+b)^3=a^3+3a^2b+3ab^2+b^3\end{align*}

を学びますが，二項定理からもこの等式が得られることを確かめておきましょう．

二項定理より

    \begin{align*}(a+b)^{3}=\Co{3}{0}a^{3}+\Co{3}{1}a^{2}b+\Co{3}{2}ab^{2}+\dots+\Co{3}{3}b^{3}\end{align*}

である．

    \begin{align*}&\Co{3}{3}=\Co{3}{0}=1,\quad \Co{3}{2}=\Co{3}{1}=3\end{align*}

なので，

    \begin{align*}(a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+\dots+b^{3}\end{align*}

を得る．

具体例２

正の整数$n$が数が大きくなるほど$(a+b)^n$を真面目に展開するのは面倒です．$(a+b)^7$くらいでも，普通に展開すると大変です．

ところが，二項定理を使えば，それほど面倒なく展開することができます．

$(a+b)^{7}$を展開せよ．

二項定理より

    \begin{align*}(a+b)^{7}=\Co{7}{0}a^{7}+\Co{7}{1}a^{6}b+\Co{7}{2}a^{5}b^{2}+\dots+\Co{7}{7}b^{7}\end{align*}

である．

    \begin{align*}&\Co{7}{7}=\Co{7}{0}=1,\quad \Co{7}{6}=\Co{7}{1}=7, \\&\Co{7}{5}=\Co{7}{2}=21,\quad \Co{7}{4}=\Co{7}{3}=35\end{align*}

なので，

    \begin{align*}(a+b)^{7}=a^{7}+7a^{6}b+21a^{5}b^{2}+35a^{4}b^{3}+35a^{3}b^{4}+21a^{2}b^{5}+7ab^{6}+b^{7}\end{align*}

を得る．

係数$\Co{n}{k}$の順番に関する注意

組み合わせの基本公式$\Co{n}{k}=\Co{n}{n-k}$を思い出すと，係数は全て逆順でもいいことが分かりますね．例えば，$(a+b)^{3}$は

    \begin{align*}(a+b)^{3}=\Co{3}{0}a^{3}+\Co{3}{1}a^{2}b+\Co{3}{2}ab^{2}+\dots+\Co{3}{3}b^{3}\end{align*}

としても

    \begin{align*}(a+b)^{3}=\Co{3}{3}a^{3}+\Co{3}{2}a^{2}b+\Co{3}{1}ab^{2}+\dots+\Co{3}{0}b^{3}\end{align*}

としても正しいですね．

また，$\Co{n}{n}=\Co{n}{0}=1$ですから，$a^n$の係数と$b^n$の係数は常に１ですね．

組み合わせの場合の数ₙCₖ｜考え方・求め方・基本性質を攻略
「６個の文字A, B, C, D, E, Fから３つ選ぶ場合の数」のように，いくつかのものからいくつかを選ぶことを「組み合わせ」と言い，場合の和では基本中の基本です．この記事では，組み合わせの場合の数の考え方と求め方を説明します．
yama-taku.science

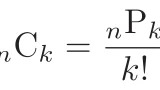
二項定理の考え方

二項定理は組み合わせの考え方を用いることで証明することができます．

証明の方針

二項定理の証明の考え方をみるために，$(a+b)^4$の展開を考えてみましょう．$(a+b)^4$は４つの$a+b$の積なので

    \begin{align*}(a+b)^4=(a+b)(a+b)(a+b)(a+b)\end{align*}

ですね．これを展開すると，各$(a+b)$から$a$または$b$のいずれかを選んでかけていくことになります．

つまり，

  1. $(\boldsymbol{\color{magenta}a}+b)(\boldsymbol{\color{magenta}a}+b)(\boldsymbol{\color{magenta}a}+b)(\boldsymbol{\color{magenta}a}+b)$の太字部分をかけて$a^4$
  2. $(\boldsymbol{\color{magenta}a}+b)(\boldsymbol{\color{magenta}a}+b)(\boldsymbol{\color{magenta}a}+b)(a+\boldsymbol{\color{magenta}b})$を太字部分をかけて$a^3b$
  3. $(\boldsymbol{\color{magenta}a}+b)(\boldsymbol{\color{magenta}a}+b)(a+\boldsymbol{\color{magenta}b})(\boldsymbol{\color{magenta}a}+b)$を太字部分をかけて$a^3b$
  4. $(\boldsymbol{\color{magenta}a}+b)(\boldsymbol{\color{magenta}a}+b)(a+\boldsymbol{\color{magenta}b})(a+\boldsymbol{\color{magenta}b})$を太字部分をかけて$a^2b^2$
  5. ……

ができあがるわけですね．

このように，４つの$a+b$から$a$か$b$を選ぶことによって全ての項が表せるわけですから，例えば$a^3b$の項は４つの$(a+b)$のうちから

  • ３つの$(a+b)$から$a$
  • １つの$(a+b)$から$b$

を取り出すことでできますね．

４つの$(a+b)$のうちから$b$を取り出す$(a+b)$を１つ選ぶ組み合わせの場合の数だけ$a^3b$ができあがるので，$a^3b$の係数は$\Co{4}{1}$となりますね．

「４つの$(a+b)$のうちから$a$を取り出す$(a+b)$を３つ選ぶ」と考えれば，$a^3b$の係数は$\Co{4}{3}$となりますね．

他の項も同様に考えれば，

    \begin{align*}(a+b)^n=\Co{4}{0}a^{4}+\Co{4}{1}a^{3}b+\Co{4}{2}a^{2}b^{2}+\Co{4}{3}ab^{3}+\Co{4}{4}b^{4}\end{align*}

が成り立つことが分かりますね．

二項定理の証明

いまの$n=4$の場合の考え方が理解できていれば，一般の$n$に対しても次のように二項定理を証明することができます．

$(a+b)^n$を展開すると，$a^n$, $a^{n-1}b$, $a^{n-2}b^2$, ……, $b^n$の項が現れる．

    \begin{align*}(a+b)^n=(a+b)(a+b)\dots(a+b)\end{align*}

の展開において，$n$個の$(a+b)$のうちから$b$を取り出す$(a+b)$を$k$個選ぶ組み合わせの場合の数だけ$a^{n-k}b^k$ができあがるので，$a^{n-k}b^k$の係数は$\Co{n}{k}$である．

よって，$(a+b)^n$は

    \begin{align*}(a+b)^n=\Co{n}{0}a^{n}+\Co{n}{1}a^{n-1}b+\Co{n}{2}a^{n-2}b^2+\dots+\Co{n}{n-1}ab^{n-1}+\Co{n}{n}b^{n}\end{align*}

と展開できる．

重複順列を使った考え方

上では組み合わせを使って二項定理を考えましたが，重複順列を使っても導出することができます．

 

$a$を$k$個と$b$を$\ell$個の合わせて$n$文字を並べることを考えます．

このとき，$abaabba\dots$という並びは

    \begin{align*}(a+b)^n=(a+b)(a+b)\dots(a+b)\end{align*}

の右辺で，

  • １つ目の$(a+b)$から$a$を
  • ２つ目の$(a+b)$から$b$を
  • ３つ目の$(a+b)$から$a$を
  • ４つ目の$(a+b)$から$a$を
  • ５つ目の$(a+b)$から$a$を
  • ……

と各$(a+b)$から$a$と$b$をどう取り出したかに対応しています．

つまり，$a$を$k$個と$b$を$\ell$個の合わせて$n$文字の並べ方と$a^{k}b^{n-k}$の個数が一致することになります．

$a$を$k$個と$b$を$\ell$個の合わせて$n$文字を並べる場合の数は

    \begin{align*}\frac{n!}{k!\ell!}=\frac{n!}{k!(n-k)!}=\Co{n}{k}\end{align*}

となって，確かに二項定理が得られましたね．

そもそも重複順列も組み合わせを用いて計算するので，上の組み合わせを使った証明と本質的には同じですね．

コメント