４つの化学の基本法則｜原子説・分子説の周辺を総まとめ

１８世紀後半ごろから，実験などによって様々な化学の基本法則が発見されてきました．

その中でも

質量保存の法則
定比比例の法則
倍数比例の法則
気体反応の法則

は今日でも頻繁に用いられ，これらなしで現在の化学を語ることはもはや不可能となっています．

私たちが原子，分子という概念にたどり着いているのも，これら化学の基本法則が契機になっています．

この記事では，原子説・分子説とこれらの契機となった上記の４つの化学の基本法則について時系列にまとめます．

おすすめ参考書
1. 理系大学受験化学の新研究(卜部吉庸著）
化学の基本法則の流れと覚え方
原子説まで
分子説まで

化学の基本法則の流れと覚え方

化学の基本法則の発見と，原子説・分子説の時代的な流れは

質量保存の法則（ラボアジエ）
定比例の法則（プルースト）
原子説（ドルトン）
倍数比例の法則（ドルトン）
気体反応の法則（ゲーリュサック）
分子説（アボガドロ）

です（かっこの中身は発見者または提唱者）．これらは

原子説まで
分子説まで

の２つのパートに分けると整理しやすいでしょう．

覚え方としては

基本法則：知って！現場気分
提唱者：ラボのフルート盗るゲーム？アホか！

など．

原子説まで

ドルトンによって原子説が提唱されるまでの流れを説明します．

質量保存の法則

１７７４年，ラボアジエ（フランス）によって質量保存の法則が発見されました．

［質量保存の法則］化学反応の前後において，物質の総質量は変化しない．

質量保存の法則は実験で簡単に確かめることができるので，小学校，中学校の理科の実験でもよく扱われますね．

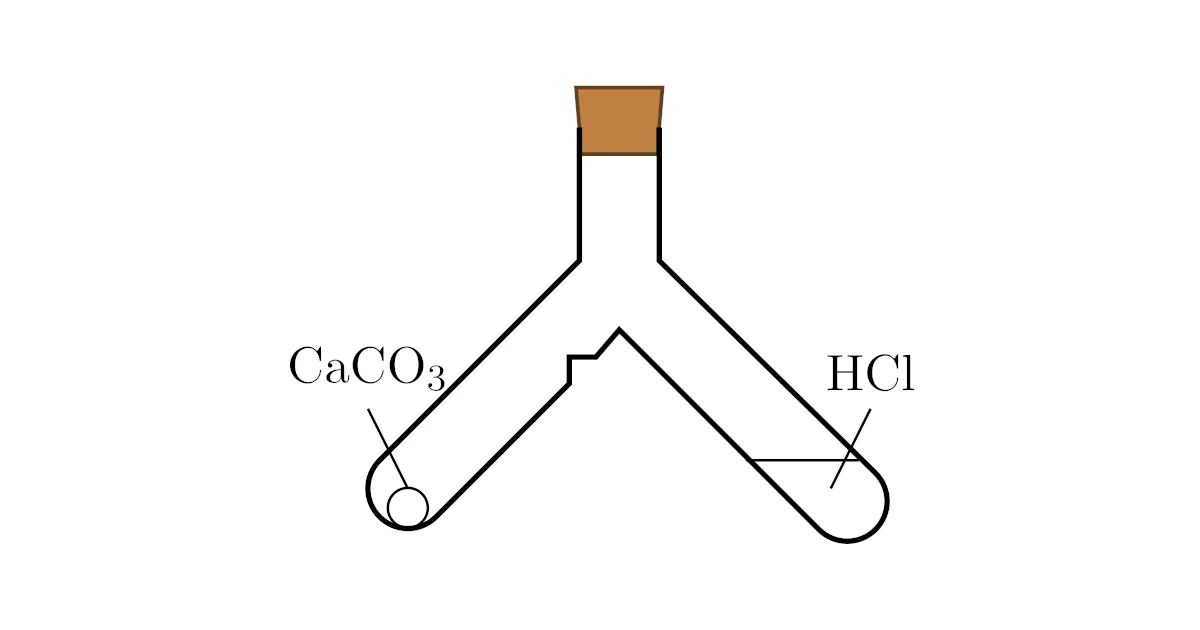
例えば，二股試験管に塩酸$\mrm{HCl}$と石灰石（炭酸カルシウム）$\mrm{CaCO_3}$を反応しないように入れて栓をします．このとき，質量を計ると全部で$100[\mrm{g}]$だったとしましょう．

その後，二股試験管を傾けて石灰石（炭酸カルシウム）$\mrm{CaCO_3}$の方に傾けて塩酸$\mrm{HCl}$を注ぐと

$\begin{align*}\mrm{CaCO_3+2HCl\to CaCl_2+CO_2+H_2O}\end{align*}$

の反応で塩化カルシウム$\mrm{CaCl_2}$，二酸化炭素$\mrm{CO_2}$，水$\mrm{H_2O}$が生じます．

この状態で質量を測るとやはり$100[\mrm{g}]$のまま変化しないというのが質量保存の法則です．

しかし，反応後に栓を抜くと発生した二酸化炭素$\mrm{CO_2}$が空気中へ抜け出るので，質量が$100[\mrm{g}]$から減少するというところまでよく問われますね．

反応を止めたいときは二股試験管を傾けることで，石灰石（炭酸カルシウム）$\mrm{CaCO_3}$がくぼみに引っかかり塩酸$\mrm{HCl}$だけを元に戻せるという点までフォローしておきましょう．

定比例の法則

１７９９年，プルースト（フランス）によって定比例の法則が発見されました．

［定比例の法則］物質Aと物質Bが同一の化合物であるとき，物質Aを構成する元素の質量比と物質Bを構成する元素の質量比はいつでも等しい．

例えば，水道水Aとカスピ海の水Bを比べたとき，これらは同一の化合物$\mrm{H_2O}$ですから，

Aの水素原子$\mrm{H}$と酸素原子$\mrm{O}$の質量比
Bの水素原子$\mrm{H}$と酸素原子$\mrm{O}$の質量比

が等しいというのが定比例の法則です．

これは水だけではなく，どんな物質に対しても全体の質量にかかわらず，構成する元素の質量比は一定であるという法則が定比例の法則です．

水$\mrm{H_2O}$について具体的な数値で言えば，水素原子$\mrm{H}$の原子数が$1$，酸素原子$\mrm{O}$の原子数が$16$であり，水$\mrm{H_2O}$に含まれる水素原子は$2$個，酸素原子は$1$個ですから，

$($水素原子$\mrm{H}$の質量$):($酸素原子$\mrm{O}$の質量$)=(1\times2):(16\times1)=1:8$

です．

原子説

質量保存の法則と定比例の法則の説明の都合で原子を用いて説明してきましたが，実はこれらの法則が発見された当時，原子説はまだ提唱されていませんでした．

すなわち，当時は「なんでかよく分からないけど，質量保存の法則と定比例の法則が成り立つ」という状況だったわけです．

そこで，ドルトン（イギリス）は

質量保存の法則：化学反応の前後において，物質の総質量は変化しない．
定比例の法則：物質Aと物質Bが同一の化合物であるとき，物質Aを構成する元素の質量比と物質Bを構成する元素の質量比はいつでも等しい．

をもとに「物質を構成する最小単位が存在すると考えると，うまくいくのではないか？」と考え，１８０３年に次の原子説を提唱しました．

[原子説]　次の１〜４をみたす粒子を原子という．

全ての物質はそれ以上分割できない粒子からなる．
各元素に対応する原子が存在し，同種の原子は同じ大きさ，質量，性質を持つ．
化合物は２種類以上の原子が一定の割合で結合してできている．
化学変化では原子の結合の仕方が変わるだけで，新たに原子が出現するのではない．

当時の科学知識でも元素という言葉は用いられていましたが，元素は「それ以上分解できない『ある性質』をもった『ナニカ』」という認識でしかありませんでした．

そこで，ドルトンは「その各元素は実は粒子である」として原子説を組み立てることで，質量保存の法則と定比例の法則を説明したわけですね．

分子説まで

次に，原子説が提唱されてから，アボガドロによって分子説が提唱されるまでの流れを説明します．

倍数比例の法則

さて，ドルトンは自身の原子説をもとに倍数比例の法則が成り立つことを予想し，実際に実験で確かめました．

［倍数比例の法則］元素$\mrm{X}$と元素$\mrm{Y}$から構成される化合物Aと化合物Bを考える．このとき，同じ質量の元素$\mrm{X}$に対して

元素$\mrm{X}$と化合して化合物Aになる元素$\mrm{Y}$の質量
元素$\mrm{X}$と化合して化合物Bになる元素$\mrm{Y}$の質量

の比は簡単な整数比になる．

例えば，炭素元素$\mrm{C}$と酸素元素$\mrm{O}$から構成される２つの化合物

一酸化炭素$\mrm{CO}$
二酸化炭素$\mrm{CO_2}$

を考えます．$10[\mrm{g}]$の炭素原子$\mrm{C}$を用意して，

一酸化炭素$\mrm{CO}$になる酸素元素$\mrm{O}$の質量を測定すると$40[\mrm{g}]$
二酸化炭素$\mrm{CO_2}$になる酸素元素$\mrm{O}$の質量を測定すると$80[\mrm{g}]$

とって，確かに$40:80=1:2$と簡単な整数比になります．

このように「[原子説]が正しければ化合物はいくつかの原子から構成されているはず．だから，質量比は原子の個数の比になるはずだから，複雑な比にはならないだろう」という発想で，「簡単な整数比になる」とドルトンは考えたわけですね．

気体反応の法則

１８０８年，ゲーリュサック（フランス）によって気体反応の法則が発見されました．

［気体反応の法則］同温，同圧のもとで，化学反応に関係する気体の体積には簡単な整数比が成り立つ．

一般に，気体の体積は温度と圧力の影響を受けやすく簡単に体積が変化するため，気体の体積を考えるときには，どのような温度，圧力のもとで計るのかを明示しておく必要があります．

そのために気体反応の法則には「同温，同圧」という条件があるわけですね．

発見された法則が成り立つ理由を考えることは科学の大切な仕事ですから，発見者のゲーリュサックは原子説を用いて気体反応の法則を説明しようとしました．

そのために，ゲーリュサックは「同温，同圧下では，同数の原子（または複合原子）からなる気体の体積は等しい」と仮定をしました．

例えば，現代では気体窒素$\mrm{N}_2$と気体酸素$\mrm{O}_2$が反応して

$\begin{align*}\mrm{2N_2+O_2 \to 2N_2O}\end{align*}$

と二酸化窒素$\mrm{N_2O}$が生じることが知られています．

ゲーリュサックが気体反応の法則を発見した当時も，化学反応式という概念はないものの

気体窒素$\mrm{X}$
気体酸素$\mrm{Y}$
二酸化窒素$\mrm{Z}$

の体積比が$2:1:2$であることは実験によって正しいことが分かっていました．

ゲーリュサックの仮定が正しければ，気体の体積比と原子（または複合原子）の個数比は一致するので，反応する気体窒素$\mrm{X}$，気体酸素$\mrm{Y}$，二酸化窒素$\mrm{Z}$の個数比も$2:1:2$です．

しかし，当時は「気体窒素は水素原子$\mrm{X}$１個で存在し，気体酸素も酸素原子$\mrm{Y}$１個で存在する」と考えられていたので，「２個の気体窒素と１個の気体酸素」から「２個の二酸化窒素」になるには，酸素原子を２つに分割しなければなりません．

しかし，原子説の１から「原子はそれ以上分割できない」ので，原子説との矛盾が起きてしまいました．

分子説

矛盾が起きてしまった以上どこかに誤りがあることになります．

１８１１年，この矛盾を解決するためアボガドロ（イタリア）は分子説を提唱しました．

［分子説］次の１〜３をみたす原子が結合したものを分子という．

気体は何個かの原子が結合してできている．
同温・同圧下では，どの気体も同体積の中には同数の分子が含まれる
分子が反応するときには原子に分かれることができる．

分子説を採用すれば，「窒素原子$\mrm{N}$が２個結合して１個の気体窒素$\mrm{N}_2$になり，酸素原子$\mrm{O}$が２個結合して１個の気体酸素$\mrm{O}_2$になっている」と考えると，先ほどの矛盾は解消されます．

アボガドロは「原子は物質を作る最小粒子，分子は物質固有の性質を失わない最小粒子」と特徴付けることで原子と分子を説明しました．

つまり，当時「気体水素$\mrm{H}_2$は水素原子$\mrm{H}$１個で存在し，気体水素$\mrm{O}_2$も酸素原子$\mrm{O}$１個で存在する」と思われていたものが間違いで，「物質はいくつかの原子が結合して初めて気体となり得る」という主張をしたことが分子説の新規性なのです．

しかし，当時この分子説はトンデモ理論だったようで，なかなか受け入れられなかったそうです．

アボガドロの法則

分子説が受け入れられるようになってくると，分子説の２はアボガドロの法則と呼ばれ，非常に重要な役割を担うことになります．

［アボガドロの法則］同温・同圧下では，気体の種類によらず同体積の中には同数の分子が含まれる．

例えば，同温・同圧下で同じ体積の水素気体$\mrm{H_2}$と酸素気体$\mrm{O_2}$があれば，この気体中の水素気体$\mrm{H_2}$と酸素気体$\mrm{O_2}$の個数は等しいというわけですね．

水素$\mrm{H_2}$と酸素$\mrm{O_2}$でなくても，どんな気体であっても体積が等しければ，同じ温度，同じ圧力のもとでは同じ個数の分子が含まれているというのがアボガドロの法則です．

アボガドロの法則は化学での気体の体積の計算などで必須なので，当たり前にしておいてください．