化学の計算を２つのタイプに分けて攻略する！

高校化学では「暗記」と「計算」の両方を必要とします．例えば

無機化学などの「暗記」に偏る分野
状態方程式などの「計算」に偏る分野

のように，化学は両方の勉強が必要な分野なので好き嫌いが分かれやすい科目のひとつです．

この記事では，暗記と計算のうちの「計算」の勉強の仕方を説明します．

計算問題の種類

化学の計算問題の多くは次の２通りに分けられます．

化学反応に無関係な計算
化学反応に関係する計算

(1)は温度や圧力や体積などを公式を用いるタイプの計算で，(2)は化学反応の物質量($\mrm{mol}$)比を考えるタイプの計算です．

分子や原子の挙動や性質を調べるのが化学なのでどうしても化学反応が絡んでくることは多いですが，必ずしも化学反応が絡むわけではありません．例えば，理想気体の状態方程式や，浸透圧の計算などは化学反応に無関係ですね．

そのような場合には，公式が必要になることが多いです．

化学反応式が絡む計算では，化学反応式から物質量($\mrm{mol}$)比を考えて計算することが多いです．

公式を使うタイプの計算

浸透圧の計算などもありますが，ここでは

ボイルの法則
シャルルの法則
ボイル・シャルルの法則

といった理想気体絡み計算について書きます．

しかし，私はこれらをあまり区別して使いません．というのは，これらは（理想気体の）状態方程式から導くことができるからです．

歴史的には(理想気体の)状態方程式の方が後なのですが，それぞれの法則がどのようなものかを理解するには（理想気体の）状態方程式から考える方が整理しやすいでしょう．

以下，考える気体は全て理想気体とします．

状態方程式

体積$V$の容器に物質量$n$，温度$T$の気体を入れたところ，圧力$P$となったとします．このとき，$\dfrac{PV}{nT}$は常に同じ値をとります．

このときの値を気体定数といい，$R$で表します．

つまり，$PV=nRT$が成り立ち，この式を状態方程式といいます．

ボイルの法則

ボイルの法則は温度$T$が一定の状態で考えます．すなわち，物質量$n$，気体定数$R$だけでなく$T$も変化しません．

このとき，$nRT$は変化しませんから，どれだけ$P$と$V$を変化させても$PV(=nRT)$は変化しません．つまり，$PV$は常に同じ値です．

ですから，$P$, $V$を$P_1$, $V_1$にしようが，$P_2$, $V_2$にしようが，$PV$は常に同じ値ですから

$\begin{align*}P_1V_1=P_2V_2\end{align*}$

が成り立ちます．

シャルルの法則

シャルルの法則は圧力$P$が一定の状態で考えます．すなわち，物質量$n$，気体定数$R$だけでなく圧力$P$も変化しません．

このとき，$\dfrac{nR}{P}$は変化しませんから，どれだけ$T$と$V$を変化させても$\dfrac{V}{T}\bra{=\dfrac{nR}{P}}$は変化しません．つまり，$\dfrac{V}{T}$は常に同じ値です．

ですから，$V$, $T$を$V_1$, $T_1$にしようが，$V_2$, $T_2$にしようが，$\dfrac{V}{T}$は常に同じ値ですから

$\begin{align*}\frac{V_1}{T_1}=\frac{V_2}{T_2}\end{align*}$

が成り立ちます．

ボイル・シャルルの法則

ボイル・シャルルの法則はボイルの法則・シャルルの法則を併せたもので，$P$, $V$, $T$のどれも一定にせずに考えます．

このとき，$nR$は変化しませんから，どれだけ$P$と$V$と$T$を変化させても$\dfrac{PV}{T}(=nR)$は変化しません．つまり，$\dfrac{PV}{T}$は常に同じ値です．

ですから，$V$, $T$を$P_1$, $V_1$, $T_1$にしようが，$P_2$, $V_2$, $T_2$にしようが，$\dfrac{PV}{T}$は常に同じ値ですから

$\begin{align*}\frac{P_1V_1}{T_1}=\frac{P_2V_2}{T_2}\end{align*}$

が成り立ちます．

化学反応式を使うタイプの計算

化学で計算が嫌いな人はこちらでつまずいている人が多い印象です．

必ず成り立つこと

次の事実は当たり前にしておきましょう．

化学反応式について，「係数の比＝物質量($\mrm{mol}$)の比」が成り立つ．

これは本当によく使いますので，必ず身につけてください．

そもそも「物質量($\mrm{mol}$)は個数を表すもの」という認識をしていることが大切です．

つまり，1２個をひとまとめにして１ダースというように，$6.0\times10^{23}$個をひとまとめにして$1[\mrm{mol}]$といっているだけです．

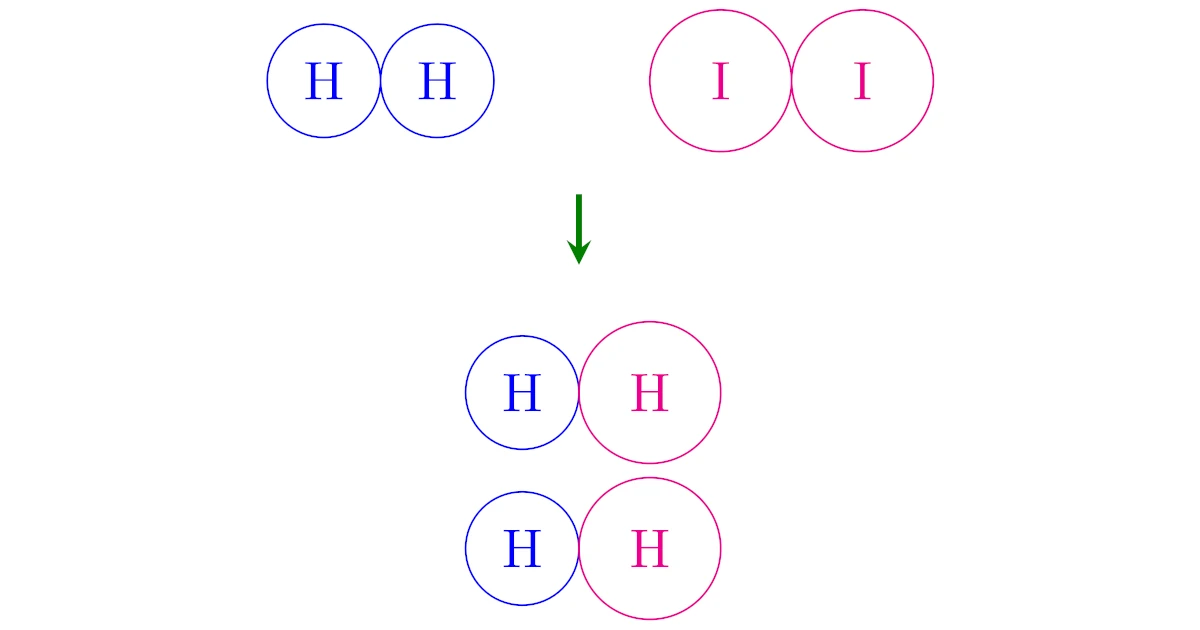
化学反応式

$\begin{align*}\mrm{H_2 + I_2 \to 2HI}\end{align*}$

は「１個の$\mrm{H_2}$と１個の$\mrm{I_2}$を反応させると，$\mrm{HI}$が２個発生する」という個数の関係を式に直したものに過ぎません．

個数が$1:1:2$となるので，

$6.0\times10^{23}$個の$\mrm{H_2}$
$6.0\times10^{23}$個の$\mrm{I_2}$

を反応させると，$\mrm{HI}$が$2\times6.0\times10^{23}$個発生するということと同じです．

さらに，$6.0\times10^{23}$個のことを$1[\mrm{mol}]$というのでしたから，これは

$1[\mrm{mol}]$の$\mrm{H_2}$
$1[\mrm{mol}]$の$\mrm{I_2}$

を反応させると，$\mrm{HI}$が$2[\mrm{mol}]$発生するということになっているわけですね．

このように，係数の比は個数の比であり，個数の比は物質量($\mrm{mol}$)比ですから，「係数の比＝物質量($\mrm{mol}$)の比」は常に使えます．

例題

「なんか『係数の比』っていろいろ等しいものあるらしいけど覚えられへん……」という人がいますが，むしろ「係数の比＝物質量($\mrm{mol}$)の比」以外を使うことはオススメしません．

まず，化学反応式から直接的に分かるのは，あくまで物質量($\mrm{mol}$)の比なので必ず物質量($\mrm{mol}$)を経由します．

標準状態で$5.6[\mrm{L}]$の$\mrm{H_2}$を，$\mrm{I_2}$と過不足なく反応させて$\mrm{HI}$を発生させた．このとき発生した$\mrm{HI}$の体積を求めよ．ただし，標準状態の気体の体積は$22.4[\mrm{L}]$であるとする．

この問題を見て，「係数の比=体積比って成り立ったっけ？」などとは考えない方がよいでしょう．

いつでも正しい「係数の比＝物質量($\mrm{mol}$)の比」のみを使えば間違えることはありません．

$\mrm{H_2}$の物質量($\mrm{mol}$)は，$\dfrac{5.6}{22.4}=\dfrac{1}{4}$より$0.25[\mrm{mol}]$である．

よって，化学反応式の係数比から$\mrm{HI}$は$2\times0.25=0.5$より$0.50[\mrm{mol}]$発生する．

したがって，$\mrm{HI}$は$22.4\times0.50=11.2$より$11.2[\mrm{L}]$発生する．

一度，$\mrm{H_2}$の体積を物質量($\mrm{mol}$)に変換してから，「係数の比＝物質量($\mrm{mol}$)の比」を使って$\mrm{HI}$の物質量($\mrm{mol}$)に変換して，体積に変換すればいいのです．

化学反応式において，「係数の比＝物質量($\mrm{mol}$)の比」はどんな場合でも正しいですから，ガンガン使ってください．

化学の計算を２つのタイプに分けて攻略する！

おすすめ参考書

理系大学受験化学の新研究(卜部吉庸著）

計算問題の種類