前々回の記事では$(a+b)^n$の展開公式である二項定理を説明しました.
二項定理は二項$a+b$に関する展開公式でしたが,これが$(a+b+c)^n$や$(a+b+c+d)^n$と項が増えたときの展開公式を多項定理といいます.
このため,多項定理は二項定理の拡張ということができます.
二項定理が場合の数の考え方を使って導出されたのと同様に,多項定理も同じく場合の数を用いて導出することができます.
この記事では
- 二項定理の考え方の復習
- 多項定理
を順に説明します.
「場合の数と確率」の一連の記事
二項定理の考え方の復習
前々回の記事の最後に二項定理の重複順列による導出を説明しました.
そもそも$(a+b)^n$は
と$n$個の$(a+b)$の積のことから,これを展開すると各$(a+b)$から$a$または$b$のいずれかを選んでかけていくことになりますね.
例えば,$n=4$のときは
- $(\boldsymbol{\color{magenta}a}+b)(\boldsymbol{\color{magenta}a}+b)(\boldsymbol{\color{magenta}a}+b)(\boldsymbol{\color{magenta}a}+b)$の太字部分をかけて$a^4$
- $(\boldsymbol{\color{magenta}a}+b)(\boldsymbol{\color{magenta}a}+b)(\boldsymbol{\color{magenta}a}+b)(a+\boldsymbol{\color{magenta}b})$を太字部分をかけて$a^3b$
- $(\boldsymbol{\color{magenta}a}+b)(\boldsymbol{\color{magenta}a}+b)(a+\boldsymbol{\color{magenta}b})(\boldsymbol{\color{magenta}a}+b)$を太字部分をかけて$a^3b$
- $(\boldsymbol{\color{magenta}a}+b)(\boldsymbol{\color{magenta}a}+b)(a+\boldsymbol{\color{magenta}b})(a+\boldsymbol{\color{magenta}b})$を太字部分をかけて$a^2b^2$
- ……
ができあがるわけですね.
そこで,例えば
の太字部分をかけるとき,このことを$aaba$と各$(a+b)$から$a$, $b$を取り出す順に並べて表すと,これは3つの$a$と1つの$b$による重複順列になっていますね.
よって,$(a+b)^4$の展開での$a^3b$の係数は,4つの$(a+b)$から$a$を3つ,$b$を1つ並べる場合の数に等しいので,$\dfrac{4!}{3!1!}=\Co{4}{1}$となるわけですね.
これを全ての$a^kb^\ell$に対して考えれば,
となるわけですね.
多項定理
$(a_1+a_2+\dots+a_r)^{n}$の展開公式である多項定理は以下の通りです.
$r$個の実数$a_1$, $a_2$,……,$a_r$と正の整数$n$に対して,$(a_1+a_2+\dots+a_r)^{n}$の$a_{1}^{n_1}a_{2}^{n_2}\dots a_{r}^{n_r}$ ($n=n_1+n_2+\dots+n_k$)の係数は
である.
多項定理の証明
いまの二項定理の重複順列による考え方と同様に多項定理を証明することができます.
$(a_1+a_2+\dots+a_r)^n$は
と$n$個の$(a_1+a_2+\dots+a_r)$の積である.
この展開における$a_1^{n_1}a_2^{n_2}\dots a_r^{n_r}$ ($n_1+n_2+\dots+n_r=n$)の係数は,$a_1$を$n_1$個,$a_2$を$n_2$個,……,$a_r$を$n_r$個並べる場合の数に等しい.
これは重複順列で場合の数は$\dfrac{n!}{n_1!n_2!\dots n_r!}$であるから,
$a_1^{n_1}a_2^{n_2}\dots a_r^{n_r}$の係数は$\dfrac{n!}{n_1!n_2!\dots n_r!}$である.
多項定理の具体例
具体的に多項定理から次の問題を解いてみましょう.
次の問いに答えよ.
- $(a+b+c)^{6}$を展開したときの$a^2b^3c$の係数を求めよ.
- $\bra{a+2+\frac{1}{a}}^{4}$を展開したときの$a^2$の係数を求めよ.
(1) 多項定理より
である.
(2) $\bra{a+2+\frac{1}{a}}^{4}$を展開したときの一般項は
である$(k+\ell+m=4)$.
いまは$a^2$の係数を問われているので$k-m=2$となる場合を考えればよく,$k+\ell+m=4$と併せると$(k,\ell,m)=(2,2,0),(3,0,1)$である.
よって,多項定理より$(k,\ell,m)=(2,2,0)$のときの項は
であり,$(k,\ell,m)=(3,0,1)$のときの係数は
なので,$\bra{a+2+\frac{1}{a}}^{4}$を展開したときの$a^2$の係数は$24+8=32$である.
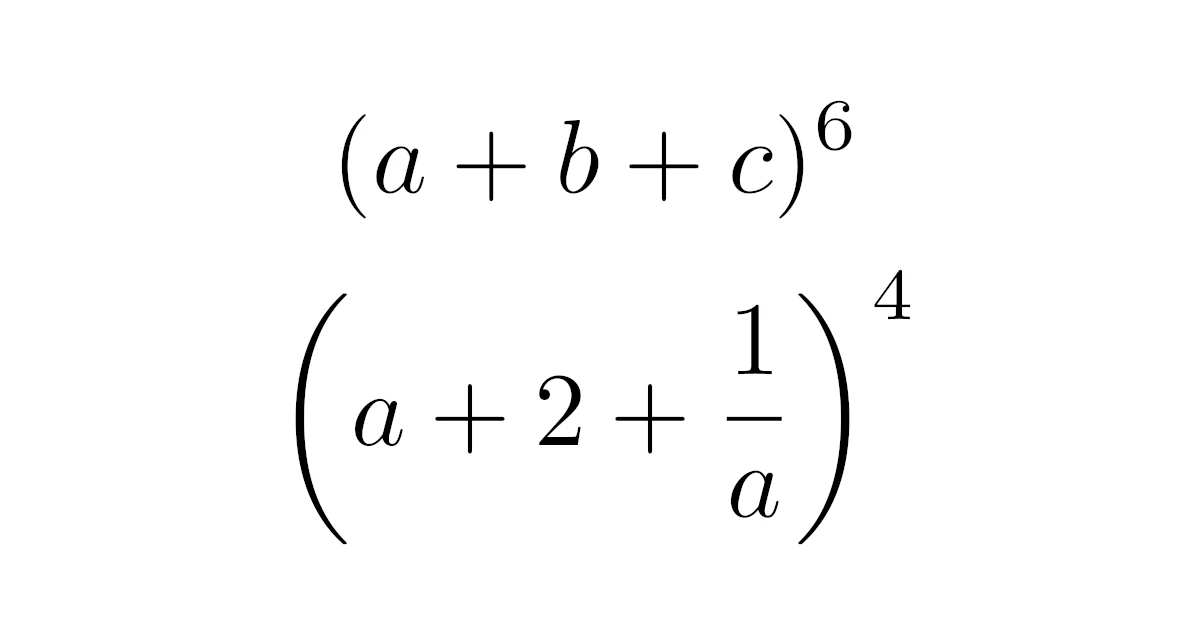
コメント