加速度と等加速度直線運動の基本｜考え方を例題から解説

物体が運動するとき，多くの場合で速度が変化します．

そのため，物体の運動を考える際には「速度がどれくらい変化するか」を表す加速度を理解することが大切です．

そこで，速度が変化する運動の中でも最も基本的な運動である等加速度直線運動があります．等加速度直線運動はその名の通り加速度が一定の運動なので，非常に考えやすい運動のひとつです．

この記事では

• 加速度
• 等加速度直線運動

を順に説明します．

加速度

加速度とはどれだけ速度が変化しているかを表すものです．

具体例から加速度を考えてみましょう．

具体例１

東向きに速さ$1\mrm{m/s}$で運動している物体$\mrm{A}$を考えます．この物体を一定の力で東向きに押して

• １秒後には東向きに速さ$2\mrm{m/s}$
• ２秒後には東向きに速さ$3\mrm{m/s}$
• ３秒後には東向きに速さ$4\mrm{m/s}$
• ……

と１秒ごとに東向きに速さが$+1\mrm{m/s}$されているとしましょう．

このとき，物体は「東向き$1\mrm{m/s^2}$の加速度で運動する」ということができます．

このように，物体の速度が単位時間でどれだけ変化するかを表すものが加速度なわけですね．

また，加速度は速度の変化なので，加速度は大きさと向きを考えるためベクトルであることに注意してください．

具体例２

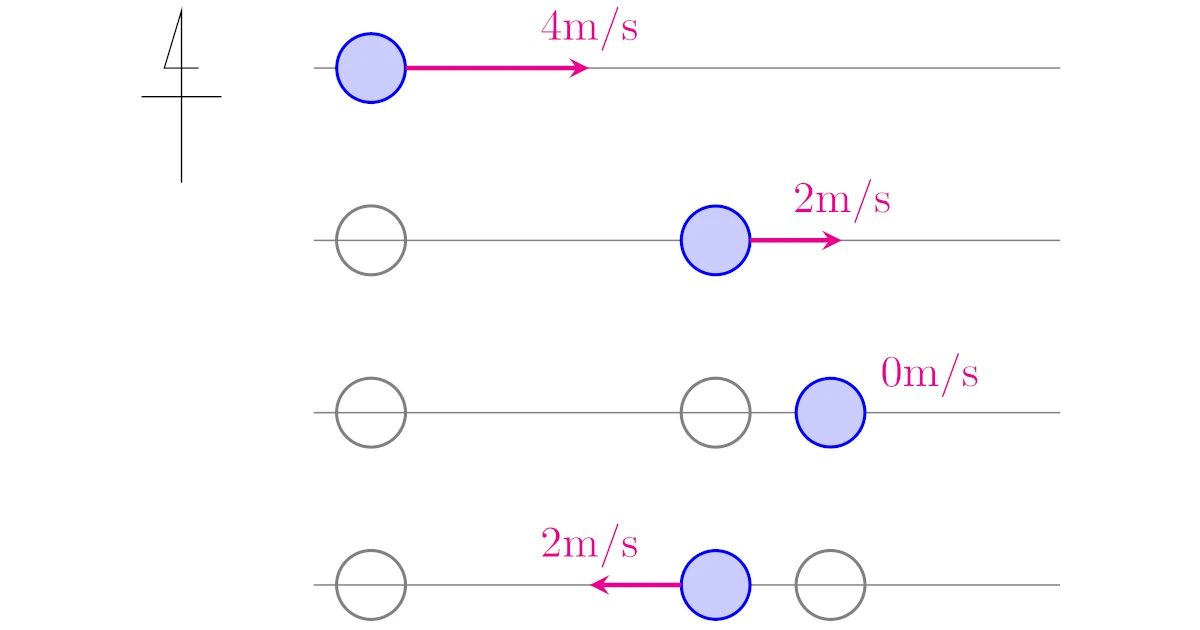
東向きに速さ$4\mrm{m/s}$で運動している物体$\mrm{A}$を考えます．この物体を一定の力で西向きに押して

• １秒後には東向きに速さ$2\mrm{m/s}$
• ２秒後には速さ$0\mrm{m/s}$
• ３秒後には西向きに速さ$2\mrm{m/s}$（東に速さ$-2\mrm{m/s}$）
• ……

と１秒ごとに西向きに速さが$+2\mrm{m/s}$されているとしましょう．イメージとしては，東向きに転がっている物体を支えて押し返しているようなものですね．

このとき，物体は「西向き$2\mrm{m/s^2}$の加速度で運動する」または「東向き$1\mrm{m/s^2}$の加速度で運動する」ということができます．

最初の速度と加速度が逆向きなので，２秒後に速さが$0\mrm{m/s^2}$になり，そのあとは西向きに運動し始めているわけですね．

等加速度直線運動

いま考えた２つの具体例は等加速度直線運動の具体例にもなっています．

等加速度直線運動の定義

上で考えた２つの具体例は

• 具体例１：初速度（最初の速度）の向きと加速度の向きが同じ向きなので，物体の運動はどんどん加速する
• 具体例２：初速度の向きと加速度の向きが逆向きなので，物体の運動はどんどん減速して一旦速度が0になり，逆向きに加速を始める

という例になっています．

このように，加速度と速度が同じ向きの場合は分かりやすいですが，逆向きの場合は一旦速度が0になって逆に進み始めることになるので注意してください．

等加速度直線運動の具体例

最も身近な等加速度直線運動の例としては物体の落下が挙げられます．

自由落下

物体からパッと手を離して落下させるとき，手を離した瞬間の速度は0ですが，時間が経つにつれてどんどん加速して落ちていきます．

実はこのときの加速度は一定であり，地球上では１秒あたり約$9.8\mrm{m/s}$ずつ加速してしていきます．すなわち，加速度の大きさが約$9.8\mrm{m/s^2}$の等加速度直線運動をします．

この$9.8[\mrm{m/s^2}]$の地球に向かう加速度のことを重力加速度といい，これについてはのちの記事で説明します．

鉛直投げ上げ

物体を真上に投げ上げた場合にも，同じく物体に重力加速度がはたらきます．

この場合には，上で見た具体例２のように投げ上げた瞬間の速度と重力加速度は逆向きになっています．

投げ上げてしばらくは真上に進みますが，どんどん減速してやがて空中で速度が0になり，加速しながら落ちてきます．