重力加速度とは何か？３種類の物体の落下を例題から理解する

等加速度直線運動の最も基本的な例に「物体の落下」があります．

物体の落下の等加速度直線運動においては，重力加速度というものが加速度となります．

この記事では，

重力加速度とは何か？
３種類の物体の落下（自由落下，鉛直投げ上げ，鉛直投げ下ろし）

を順に解説します．

「直線運動の基本」の一連の記事

重力加速度とは何か？
3種類の物体の落下
座標の向きを逆にするとどうなるのか？

重力加速度とは何か？

まずは物体の落下における加速度が，どんな物体でも一定であることを説明します．

落下の加速度

次の問題を考えてみてください．

$1\mrm{kg}$の金属$\mrm{A}$と$10\mrm{kg}$の金属$\mrm{B}$をスカイツリーの頂上から同じ高さで手を離し，自由落下させる．このとき次のうち正しいものを選べ．ただし，空気抵抗は無視する．

金属$\mrm{A}$が先に地面に到達する
金属$\mrm{B}$が先に地面に到達する
金属$\mrm{A}$と金属$\mrm{B}$は同時に地面に到達する

この問題に対して，ガリレオ・ガリレイは以下のような[ピサの斜塔の実験]を行いました．

［ピサの斜塔の実験］ピサの斜塔上の同じ高さから重さの違う２つの物体を落下させ，地面に到達する時間が同じであるかどうかをみるために行った実験．

実験の結果，２つの球はほぼ同時に地面に到達した．

[ピサの斜塔の実験]から上の問題の答えは(3)であることが分かりますが，直感に合わないと思う人がいるかもしれません．

確かに家の２階から紙と鉄球を同時に落下させると，おそらく鉄球の方が圧倒的に早く地面に到達しますが，これは空気抵抗があることが原因です．

例えば，空気が無視できる火星上で同じことをすれば，紙と鉄球は同時に地面に到達します．

このように，空気抵抗が無視できる条件下の自由落下では，重さに関係なく同じ加速度の等加速度運動をすることは当たり前にしておきたいところです．

直感的な理由

「実験でそうなったからそうだ！」というのも気持ち悪いですから，次のように考えてみると納得できるかもしれません．

例えば，全く同じ$1\mrm{kg}$の鉄球と$1\mrm{kg}$の鉄球を同時に落とすと，これは同時に地面に到達しますね．

ここで，この２つの鉄球を接着剤でくっつけて落とすとどうでしょうか？

くっつけられた２つの$1\mrm{kg}$の鉄球は，それぞれが$1\mrm{kg}$の鉄球として落下するので，普通の$1\mrm{kg}$の鉄球と同時に地面に到着します．

接着剤でくっつけた２つの鉄球は合わせて$2\mrm{kg}$の質量をもちますが，落下の仕方は$1\mrm{kg}$の鉄球と変わりません．

このことから「質量によって落下の様子は変わらない」ことが見てとれますね．

重力加速度

実はこの物体の落下は（空気抵抗を無視すると）等加速度直線運動になっています．

このとき，質量によらず同じように落下するということは，どの物体にも同じだけの加速度がかかっているということになります．

つまり，地球上の物体の落下には，固有の加速度があるということになります．

物体が落下するときの等加速度直線運動の加速度を重力加速度という．

地球上では重力加速度の大きさは約$9.8\mrm{m/s^2}$です．

重力加速度の大きさは地球上で一様に同じ値というわけではありません．地球の極付近と赤道付近でも変わってきます．

また，我々は日常的に「下」という言葉を使いますが

日本にいる我々が地面を指して言う「下」
地球の反対側の人々が地面を指して言う「下」

は逆向きですね．そこで，物理では地面に向かう「下」を次のように表現します．

地球の中心に向かう向きを鉛直下向きといい，地球の中心から離れる向きを鉛直上向きという．鉛直上向き，鉛直下向きを合わせて鉛直方向という．

この言葉を使うと「重力加速度の向きは鉛直下向き」といえますね．

3種類の物体の落下

物体の落下には

自由落下
鉛直投げ上げ
鉛直投げ下ろし

の３パターンがあります．

原理的にはこれらは同じものですが，最初はこれらを別々に理解した方が分かりやすいことが多いので，この記事ではこれら３パターンを分けて説明します．

先ほど説明したように物体の落下は等加速度直線運動なので，以下では等加速度直線運動の基本公式を思い出しておきましょう：

$\begin{align*}\begin{cases}v=v_{0}+at \\x=v_{0}t+\frac{1}{2}at^2 \\v^2-{v_0}^2=2ax\end{cases}\end{align*}$

物体の落下においては，これらの関係式での加速度$a$が重力加速度となるわけですね．

自由落下

パッと手を離して物体を落下させるような，初速度が０の物体の落下を自由落下といいます．

高さ$490\mrm{m}$の上空で小球を持った手を離し，小球を静かに落下させる．

地面に小球が到達するのは，手を離してから何秒後か求めよ．
地面に小球が到達したとき，小球の速さを求めよ．

ただし，重力加速度は$9.8\mrm{m/s^2}$であるとし，空気抵抗は無視する．

鉛直下向きを正方向，小球を離した位置を原点とし，

小球が地面に到達するまでの時間を$t[\mrm{s}]$
小球が地面に到達したときの速さを$v[\mrm{m/s}]$

とおく．このとき，初速度は$v_{0}=0\mrm{m/s}$，地面に到達したときの変位は$x=490\mrm{m}$，重力加速度は$g=9.8\mrm{m/s^2}$である．

(1) 変位$x$と時間$t$の関係式$x=v_0t+\dfrac{1}{2}at^2$より，

$\begin{align*}490=0\times t+\dfrac{1}{2}\times 9.8\times t^2\end{align*}$

だから，$t^2=100$となり$t>0$より$t=10$を得る．すなわち，10秒後に小球は地面に到達する．

(2) 速度$v$と時間$t$の関係式である$v=v_0+at$より，

$\begin{align*}v=0+9.8\times 10=98\end{align*}$

を得る．すなわち，小球は速さ$98\mrm{m/s}$で地面に到達する．

鉛直投げ下ろし

物体に鉛直下向きの初速度を与える物体を落下を鉛直投げ下ろしといいます．

ある高さから小球を速さ$19.6\mrm{m/s}$で鉛直下向きに投げる．その後，小球が地面に到達したとき，小球の速さは$98\mrm{m/s}$であることが観測された．

小球を投げ下ろした地点の高さを求めよ．
小球が地面に到達するのは，投げ下ろしてから何秒後か求めよ．

ただし，重力加速度は$9.8\mrm{m/s^2}$であるとし，空気抵抗は無視する．

鉛直下向きを正方向，小球を投げ下ろした位置を原点とし，

小球を投げ下ろした地点の高さを$x[\mrm{m}]$
小球が地面に到達するまでの時間を$t[\mrm{s}]$

とおく．このとき，初速度は$v_{0}=19.6\mrm{m/s}$，地面に到達したときの速度は$v=98\mrm{m/s}$，重力加速度は$g=9.8\mrm{m/s^2}$である．

(1) 変位$x$と速度$v$の関係式である$v^2-{v_0}^2=2ax$より，

$\begin{align*}98^2-19.6^2=2\times 9.8\times x\end{align*}$

だから$x=470.4$を得る．すなわち，小球を投げ下ろした高さは$470.4\mrm{m}$である．

(2) 時間$t$と速度$v$の関係式である$v=v_0+at$より，

$\begin{align*}98=19.6+9.8\times t\end{align*}$

だから$t=8$を得る．すなわち，小球を投げ下ろして$8$秒後に小球は地面に到達する．

鉛直投げ上げ

物体に鉛直上向きの初速度を与える物体を落下を鉛直投げ上げといいます．

ある高さから小球を速さ$19.6\mrm{m/s}$で鉛直上向きに投げる．その後，小球が地面に到達したとき，小球の速さは$98\mrm{m/s}$であることが観測された．

小球を投げ上げた地点の高さを求めよ．
小球が地面に到達するのは，投げ上げてから何秒後か求めよ．

ただし，重力加速度は$9.8\mrm{m/s^2}$であるとし，空気抵抗は無視する．

鉛直下向きを正方向，小球を投げ上げた位置を原点とし，

小球を投げ上げた地点の高さを$x[\mrm{m}]$
小球が地面に到達するまでの時間を$t[\mrm{s}]$

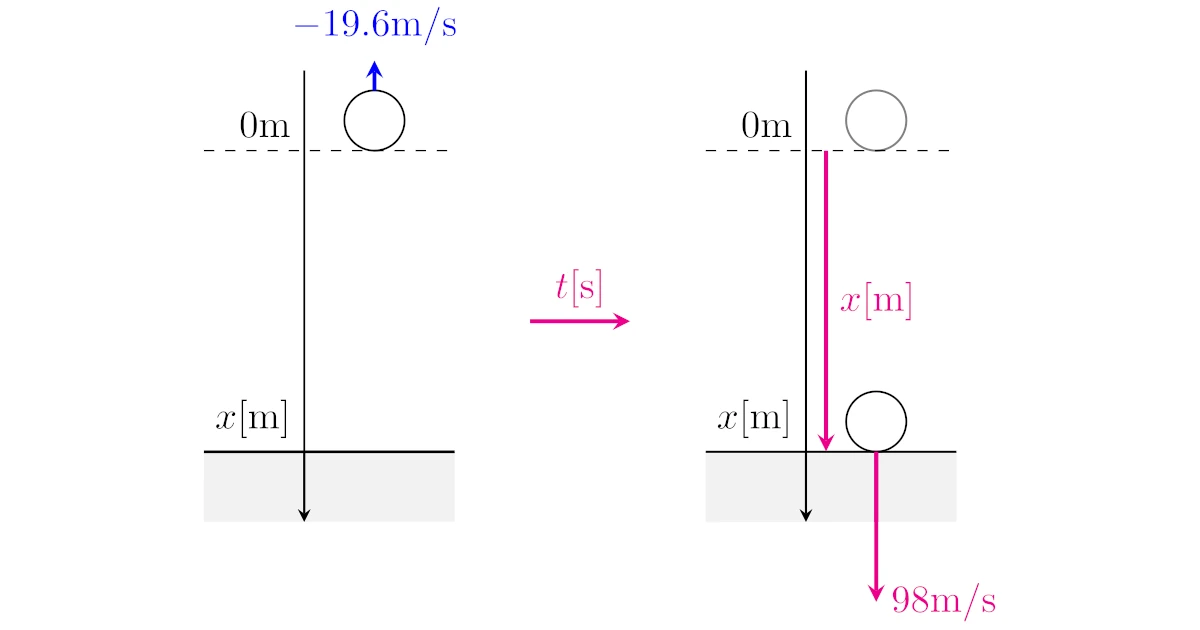
とおく．このとき，初速度は$v_{0}=-19.6\mrm{m/s}$，地面に到達したときの速度は$v=98\mrm{m/s}$，重力加速度は$g=9.8\mrm{m/s^2}$である．

(1) 変位$x$と速度$v$の関係式である$v^2-{v_0}^2=2ax$より，

$\begin{align*}98^2-(-19.6)^2=2\times 9.8\times x\end{align*}$

だから$x=470.4$を得る．すなわち，小球を投げ上げた地点の高さは$470.4\mrm{m}$である．

(2) 時間$t$と速度$v$の関係式である$v=v_0+at$より，

$\begin{align*}98=-19.6+9.8\times t\end{align*}$

だから$t=12$を得る．すなわち，小球を投げ上げて$12$秒後に小球は地面に到達する．

座標の向きを逆にするとどうなるのか？

上の具体例ではいずれも鉛直下向きを正に座標をとって考えました．

しかし，鉛直投げ上げの場合には初速度が鉛直上向きなので，鉛直上向きが正の座標をとりたい方もいるかもしれません．

実は座標の向きを逆にとっても本質的には何も変わらず，同じように答えを導くことができます．

上の鉛直投げ上げの問題で，鉛直上向きを正に座標をとって考えてみましょう．

（再掲）ある高さから小球を速さ$19.6\mrm{m/s}$で鉛直上向きに投げる．その後，小球が地面に到達したとき，小球の速さは$98\mrm{m/s}$であることが観測された．

小球を投げ上げた地点の高さを求めよ．
小球が地面に到達するのは，投げ上げてから何秒後か求めよ．

ただし，重力加速度は$9.8\mrm{m/s^2}$であるとし，空気抵抗は無視する．

鉛直上向きを正方向，小球を投げ上げた位置を原点とし，

小球を投げ上げた地点の高さを$x[\mrm{m}]$
小球が地面に到達するまでの時間を$t[\mrm{s}]$

とする．このとき，初速度は$v_{0}=19.6\mrm{m/s}$，地面に到達したときの速度は$v=-98\mrm{m/s}$，重力加速度は$g=-9.8\mrm{m/s^2}$である．

(1) 変位$x$と速度$v$の関係式である$v^2-{v_0}^2=2ax$より，

$\begin{align*}(-98)^2-19.6^2=2\times(-9.8)\times x\end{align*}$

だから$x=-470.4$を得る．すなわち，小球を投げ上げた地点の高さは$470.4\mrm{m}$である．

(2) 時間$t$と速度$v$の関係式である$v=v_0+at$より，

$\begin{align*}-98=19.6+(-9.8)\times t\end{align*}$

だから$t=12$を得る．すなわち，小球を投げ上げて$12$秒後に小球は地面に到達する．

鉛直上向きを正に座標をとると，鉛直下向きの速度や重力加速度は負になるわけですね．

速度や重力加速度は向きも併せて考えるベクトルなので正負に気をつけなければなりませんが，座標の向きは本質的にはどちらでも良いわけですね．