条件付き確率とは「ある事象が起こったことが分かっているもとでの確率」のことをいいます.
条件付き確率は直感に合わない人が少なくないようで,確率を勉強するときに避けられがちな分野のひとつです.
この記事では条件付き確率の具体的な問題をもとに
- よくある間違い
- 正しい考え方
を解説します.
また,同時に多くの人が苦手とする同様に確からしいという概念についても説明します.
条件付き確率の例
3枚のカードS, T, Uの両面は
- S:両面とも赤
- T:両面とも青
- U:片面が赤で他面が青
と色が塗られているとする.
このとき,S, T, Uを1枚ずつ箱に入れ,無作為に1枚取り出す.
(1) Uを選ぶ確率を求めよ.
(2) 机に置くと上面が赤であった.このとき,このカードの下面が青である確率を求めよ.
(1)も(2)も結局はUのカードを選ぶ確率ですが,(2)は「机に置くと片面が赤であった」という条件のもとでのUを選ぶ条件付き確率です.
つまり,「とりあえず上面は赤でした」という条件のもとで「このときの裏が青である確率はどれくらいですか?」ということが問われているのが(2)なわけですね.
一方,(1)は何も条件がないので,単に3枚のうちからUを選ぶ確率ですから,(1)の答えは$\dfrac{1}{3}$です.
問題は(2)ですね.
条件付き確率の考え方
クラス授業でこの問題を解いてもらうと,答えはたいてい
- $\dfrac{1}{2}$と答える人
- $\dfrac{1}{3}$と答える人
に分かれます.
先に結論を書くと$\dfrac{1}{3}$が正しく,$\dfrac{1}{2}$は間違いです.
間違った考え方
間違った答え$\dfrac{1}{2}$を導いてしまう人は次のように考える人が多いようです.
「片側が赤のとき,その裏は「赤」か「青」の2通り.よって,求める確率は$\dfrac{1}{2}$である.」
しかし,「片面が赤のとき,その裏が『赤』であることと,『青』であることが同様に確からしくない」のでこの考え方は間違いです.
「出た!同様に確からしい!」と思った人もいるかもしれません.
「同様に確からしい」の説明はひとまずおいて,次に正しい考え方を説明します.
正しい考え方
正しい答え$\dfrac{1}{3}$を導くには次のように考えます.
上面が赤なら,この赤は
- Sの表
- Sの裏
- Uの赤面
の3通りで,これらは同様に確からしく起こる.
このうち,裏が青なのは最後の1通りだから,求める確率は$\dfrac{1}{3}$である.
「片面が赤であった」という条件がありますが,この赤が
- Sの表なのか
- Sの裏なのか
- Uの赤面なのか
が分かりません.しかし,これらのどれであるのかは当確率です.
ですから,この3通りの中で裏が青であるのは1通りなので,求める確率は$\dfrac{1}{3}$となるわけです.
「間違った考え方」が間違っている理由
では,「間違った考え方」のどこが間違いなのでしょうか?
実は「片側が赤のとき,裏は『赤』か『青』の2通り」と考えたところまでは正しいのですが,ここから「確率は$\dfrac{1}{2}$」と結論付けたところが誤りです.
場合の数が2通りであっても,確率が$\dfrac{1}{2}$とは限らないというところがポイントです!
このことに納得できない人は,次の問題を考えてみてください.
表裏が均等なコインを折り曲げたとき,表が出る確率は$\dfrac{1}{2}$か?
この問題でも「コインは『表』か『裏』の2通り」であることは正しいのですが,「表が出る確率は$\dfrac{1}{2}$」というのは誤りですね.
このように,場合が2通りであっても,それぞれの場合が均等に起こらない場合には,それぞれの確率が$\dfrac{1}{2}$とは言えないわけですね.
「同様に確からしくない」からの説明
同様に確からしいとは「どの事象も等しい頻度で起こる」ということをいいます.
例えば,上のコインの問題では表が出る事象と裏が出る事象は同様に確からしくないので,もちろん場合の数が2通りであっても確率は$\dfrac{1}{2}$とは言えないわけです.
一方で「サイコロを振って1の目が出る確率は$\dfrac{1}{6}$」と言えるのは,どの目も等しい頻度で起こると考えているからなんですね.
さて,最初の問題に話を戻しましょう.
(再掲)3枚のカードS, T, Uの両面は
- S:両面とも赤
- T:両面とも青
- U:片面が赤で他面が青
と色が塗られているとする.
このとき,S, T, Uを1枚ずつ箱に入れ,無作為に1枚取り出す.
(1) Uを選ぶ確率を求めよ.
(2) 机に置くと上面が赤であった.このとき,このカードの下面が青である確率を求めよ.
この(2)を考えたとき,上面の赤が
- Sの表
- Sの裏
- Uの赤面
のどれが起こる頻度も等しいです.つまり,これらの事象は同様に確からしいですから,求める確率は$\dfrac{1}{3}$と言えるわけですね.
一方,片面が赤のときに
- 裏が赤である事象
- 裏が青である事象
は同様に確からしくないので,確率が$\dfrac{1}{2}$とは言えないわけですね.
条件付き確率の公式
さて,ここで一度具体例から離れて,次の条件付き確率を求める公式を紹介します.
公式とその導出
事象$\mrm{S}$が起こる場合の数を$n(\mrm{S})$,事象$\mrm{S}$が起こる確率を$P(\mrm{S})$と表すことにしましょう.
[条件付き確率の公式] 全事象を$\mrm{U}$とし,それぞれの場合は同様に確からしいとする.事象$\mrm{A}$と事象$\mrm{B}$に対し,$\mrm{A}$が起こった後に$\mrm{B}$が起こる条件付き確率$P_{\mrm{A}}(\mrm{B})$は
である.
「全体の場合の数」は下図の色塗り部分で$n(\mrm{A})$である.
「Aが起こったことが確定したあとにBが起こる場合の数」は下図の色塗り部分で$n(\mrm{A}\cap\mrm{B})$である.
よって,$P_{\mrm{A}}(\mrm{B})$はAが起こったことが確定したあとにBが起こる確率だから
である.分母分子を$n(\mrm{U})$で割って
が得られる.
問題の(2)では事象Aを「上面が赤である」,事象Bを「裏が青である」として,$P_{\mrm{A}}(\mrm{B})$を求めれば良いことが分かります.
公式を用いた解答
この公式を用いて,最初の問題を解きましょう.
カードS, T, Uの選び方が3通り,裏表の選び方がそれぞれ2通りなので,全ての場合の数は6通りである.
- 事象$\mrm{A}$を「カードを机に置くと机に置くと上面が赤となる事象」
- 事象$\mrm{B}$を「机に置いたカードの下面が青となる事象」
とすると,求める確率は条件付き確率$\mrm{P}_A(B)$である.
事象$\mrm{A}\cap\mrm{B}$は「上面が赤で,裏面が青である事象」であり,これはカードTが赤面を上面として机に置かれた場合の1通りなので,
である.また,事象$\mrm{A}$はカードSの裏と表の2通りと,カードTが赤を上面として机に置かれた1通りの合わせて3通りなので,
である.したがって,求める確率は
である.
確かに$\dfrac{1}{3}$になりましたね!
補足
公式を使うために公式に沿って丁寧に求めましたが,実は$P(\mrm{A}\cap\mrm{B})$と$P(\mrm{A})$まで求める必要はありません.
公式の証明を読めば分かるように,
ですから,実は$n(\mrm{A}\cap\mrm{B})$と$n(\mrm{A})$さえ分かっていれば(2)の確率は求まります.
でしたから,ここから$P_{\mrm{A}}(\mrm{B})=\dfrac{1}{3}$が得られますね.
条件付き確率は少し慣れが必要なので,実際に問題を解いて感覚を身に付けてください.
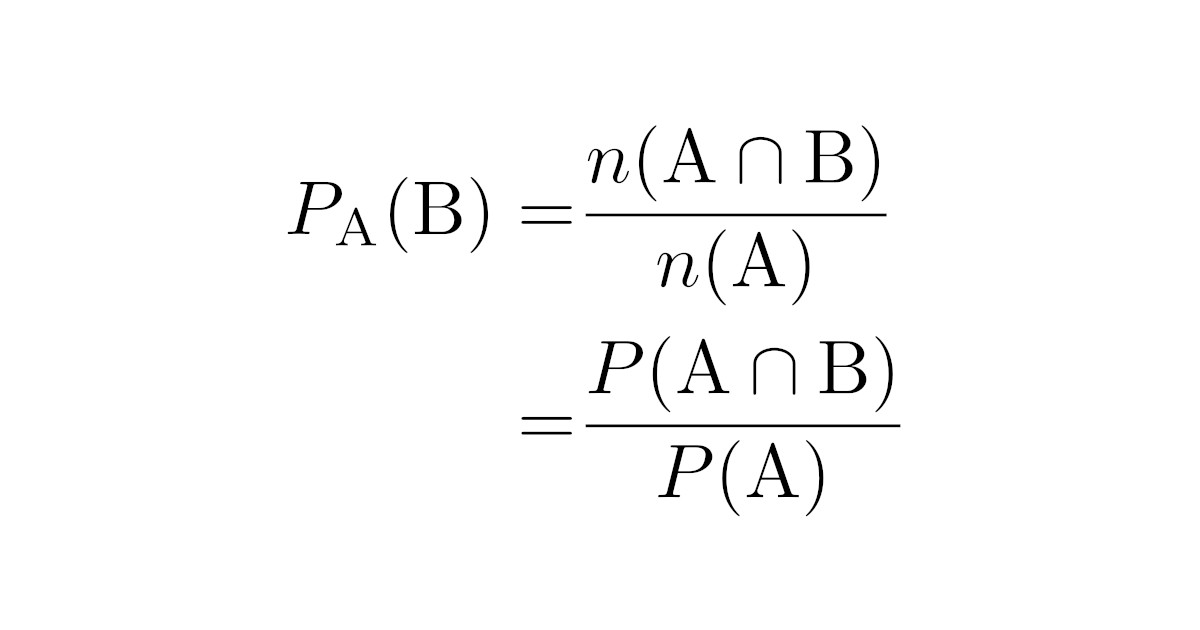
コメント