前回の記事では$(a+b)^n$が
と展開されるという二項定理を説明しました.
さて,実はこの二項係数$\Co{n}{k}$はパスカルの三角形と呼ばれるものとピッタリ対応することが分かります.
この記事では
- 二項係数$\Co{n}{k}$の性質
- パスカルの三角形
- 二項定理とパスカルの三角形の関係
を順に説明します.
「場合の数と確率」の一連の記事
二項係数の性質
まずは二項係数$\Co{n}{k}$に関する重要性質を3つ紹介します.
二項係数$\Co{n}{k}$について,次の性質が成り立つ.
- $(n-k)\Co{n}{k}=(k+1)\Co{n}{k+1}$
- $(n+1)\Co{n}{k}=(n-k+1)\Co{n+1}{k}$
- $\Co{n}{k}+\Co{n}{k+1}=\Co{n+1}{k+1}$
ざっくり言えば,
- (1)は$\Co{n}{k}$と$\Co{n}{k+1}$の関係式($\Co{n}{k}$の$k$を1つずらしたときにどうなるか)
- (2)は$\Co{n}{k}$と$\Co{n+1}{k}$の関係式($\Co{n}{k}$の$n$を1つずらしたときにどうなるか)
を表していますね.
また,(3)は(1)と(2)を用いて示すことができますが,この(3)がこの記事のメインテーマのパスカルの三角形と密接に関係しています.
これら(1)〜(3)の証明には以前の記事で証明した$\Co{n}{k}=\dfrac{n!}{(n-k)!k!}$を用いるので,ここで思い出しておきましょう.
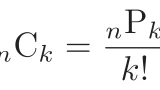
(1) $\Co{n}{k}=\dfrac{n!}{(n-k)!k!}$, $\Co{n}{k+1}=\dfrac{n!}{(n-k-1)!(k+1)!}$より
だから,$(n-k)\Co{n}{k}=(k+1)\Co{n}{k+1}$が従う.
(2) $\Co{n}{k}=\dfrac{n!}{(n-k)!k!}$, $\Co{n+1}{k}=\dfrac{(n+1)!}{(n-k+1)!k!}$より
だから,$(n+1)\Co{n}{k}=(n-k+1)\Co{n+1}{k}$が従う.
(3) 性質(1)から$\Co{n}{k}=\dfrac{k+1}{n-k}\Co{n}{k+1}$が成り立ち,性質(2)から$\Co{n}{k+1}=\dfrac{n-k}{n+1}\Co{n+1}{k+1}$が成り立つから,
が従う.
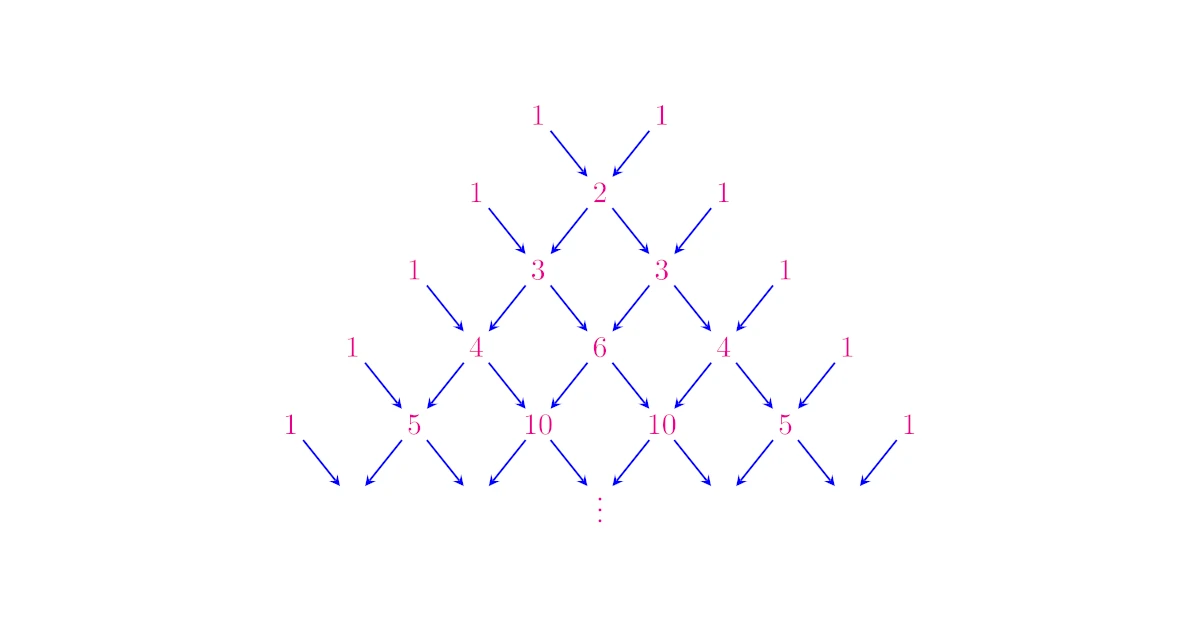
パスカルの三角形
次にパスカルの三角形がどういうものか説明します.
このパスカルは「人間は考える葦である」や気圧の単位で有名なBlaise Pascal氏です.
次の条件で順次定まっていく整数の並びをパスカルの三角形という.
- 上から$n$段目には$(n+1)$個の整数が並ぶ
- どの段も両端は$1$である
- $(n+1)$段目の左から$(r+1)$番目の整数は,$n$段目の左から$r$番目,$(r+1)$番目の整数の和である
$1$段目の$1$, $1$から出発して,$2$段目,$3$段目,……と順に整数を並べていくわけですね.
ここで,$(a+b)^n$を展開したときの係数を$n$ごとに観察すると,
- $(a+b)^1=a+b$の係数は$1$, $1$
- $(a+b)^2=a^2+2ab+b^2$の係数は$1$, $2$, $1$
- $(a+b)^3=a^3+3a^2b+3ab^2+b^3$の係数は$1$, $3, $3$, $1$
となっており,これはパスカルの三角形の上からの整数の並びとぴったり一致していることがみてとれますね!
二項定理とパスカルの三角形の関係
ということで,次の定理が成り立つことが見てとれますね.
パスカルの三角形の$n$段目は,$(a+b)^n$の二項展開の$a^n$, $a^{n-1}b$,……,$b^n$の係数の並びに一致する.
証明
この証明のために,上で示した二項係数$\Co{n}{k}$の性質(3)が本質的に重要です.
$n=1,2,\dots$に対して,$(a+b)^n$の二項展開の$a^n$, $a^{n-1}b$,……,$b^n$の係数を$n$段目に並べると
となっている.このとき,上から$n$段目には$(n+1)$個の整数が並んでおり,どの段も両端は$1$である.
さらに,上で示した二項係数$\Co{n}{k}$の性質(3)より
が成り立つから,$(n+1)$段目の左から$(r+1)$番目の整数$\Co{n+1}{r+1}$は,$n$段目の左から$r$番目,$(r+1)$番目の整数$\Co{n}{r}$, $\Co{n}{r+1}$の和である.
よって,上の数の並びはパスカルの三角形である.
つまり,等式$\Co{n}{r}+\Co{n}{r+1}=\Co{n+1}{r+1}$でどんどん繋がって,パスカルの三角形になっているわけですね.
具体例
具体的に以下の展開を求めましょう.
$(a+b)^7$を展開せよ.
パスカルの三角形の$7$段目を見れば,$(a+b)^7$を展開したときの$a^7,a^6b,\dots,b^7$の係数が分かる.
よって,
である.
これは前回の記事で二項定理を用いて展開した$(a+b)^7$の結果と一致していますね.
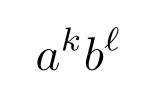
このように具体的な(それほど大きくない)正の整数$n$に対する$(a+b)^n$の展開はパスカルの三角形を使うと簡単に計算することができますね.
コメント