場合の数では「いくつかのモノを並べる総数」を求める問題は基本問題としてよく出題されます.
例えば,次のような問題はどう考えればよいでしょうか?
9枚のカード$\fbox{1}\fbox{2}\fbox{3}\dots\fbox{8}\fbox{9}$から
のように$2$枚を選んで,並べる場合の数を求めよ.
一般にいくつかのモノを(一列に)並べることを順列といいます.
順列は場合の数の中で最も基本的なもののひとつなので,考え方から理解しておきましょう.
この記事では,
- 順列の考え方
- 順列の場合の数$\Pe{n}{k}$
- 階乗$n!$
を順に説明します.
「場合の数と確率」の一連の記事
順列の考え方
まずは冒頭の問題を考えましょう.
具体例1(9枚のカードから2枚選んで並べる)
9枚のカード$\fbox{1}\fbox{2}\fbox{3}\dots\fbox{8}\fbox{9}$から2枚選んで並べる場合の数を求めよ.
場合の数の基本は樹形図を考えてからの数え上げでしたね.最初なので丁寧に考えましょう.
9枚のカード$\fbox{1}\fbox{2}\fbox{3}\dots\fbox{8}\fbox{9}$で2桁の整数を作る場合の数を求めれば良い.
たとえば,1の位の数が$\fbox{1}$なら,10の位の数は$\fbox{1}$以外の8通りある.
1の位の数が$\fbox{1}$でなくても同様に,それぞれの場合で10の位の数は8通りある.
よって,以上の樹形図から,求める場合の数は$9\times 8=72$である.
ポイントは10の位の数としてどの数を持ってきても,1の位の数は8通りあるという点ですね.
具体例2(9枚のカードから3枚選んで並べる)
9枚のカード$\fbox{1}\fbox{2}\fbox{3}\dots\fbox{8}\fbox{9}$から3枚選んで並べる場合の数を求めよ.
状況は同じですが,今度は3枚のカードを並べることを考えます.
上の問題で考えた順列に加えて,100の位の数のカードを加えて考えればよい.
1の位の数,10の位の数のカードを選ぶと,100の位の数の選び方は7通りある.
よって,同様に樹形図を考えて,求める場合の数は$9\times 8\times7=504$である.
順列の場合の数$\Pe{n}{k}$の定義・性質
一般に,モノを(一列に)並べることを順列といいます.
上の具体例の考え方を一般化すると,順列の場合の数は次のように求めることができますね.
正の整数$n$, $k$は$k\leqq n$を満たすとする.このとき,$n$個のものから$k$個選んで並べる場合の数は
である.
順列の場合の数$\Pe{n}{k}$
この順列はよく現れるので次のように記号$\Pe{n}{k}$を定めましょう.
$n$個のものから$k$個選んで並べる場合の数を$\Pe{n}{k}$で表す.すなわち,
である.また,$k=0$のときは$\Pe{n}{0}=1$と定める.
$\Pe{n}{k}$の$\mrm{P}$は順列を意味する“Permutation”の頭文字“P”に由来します.
例えば,
- 上の具体例1の「異なる9枚のカードから2枚選んで並べる場合の数」は$\Pe{9}{2}$
- 上の具体例2の「異なる9枚のカードから3枚選んで並べる場合の数は$\Pe{9}{3}$
ですね.
他にも,例えば異なる5枚のカードから3個を選んで並べる場合の数は$\Pe{5}{3}$で,これは
と計算できますね.
階乗$n!$
順列の記号$\Pe{n}{k}$に関して,特に$k=n$の場合には階乗と呼ばれます.
$n$を正の整数とする.1から$n$までの整数全部の積を$n!$で表し,$n$の階乗 (factorial)という.すなわち,
である.また,$n=0$のときは$0!=1$と定める.
つまり,$n$の階乗$n!$は「$n$個のものを全部並べる場合の数」を表すわけですね.
さて,$\Pe{n}{k}$は階乗を用いると,次のようにスッキリ表せます.
正の整数$n$と負でない整数$k$は$k\leqq n$を満たすとする.このとき,
が成り立つ.
$0<k<n$のとき,$k=0$のとき,$k=n$のときに分けて示す.
[1]$k$が$0<k<n$を満たすとき,
が成り立つ.
[2]$k=0$のときは$\Pe{n}{k}=1$と定義されており,
なので$\Pe{n}{k}=\dfrac{n!}{(n-k)!}$が成り立つ.
[3]$k=n$のときは$\Pe{n}{k}=n!$であり,$0!=1$と定義されているから
なので$\Pe{n}{k}=\dfrac{n!}{(n-k)!}$が成り立つ.
[1]では$\Pe{n}{k}=n(n-1)\dots(n-k+1)$を階乗で表すために,分子が$n!$になるために足りない$(n-k)!=(n-k)(n-k-1)\dots2\cdot1$を分母分子にかけているのがポイントですね.
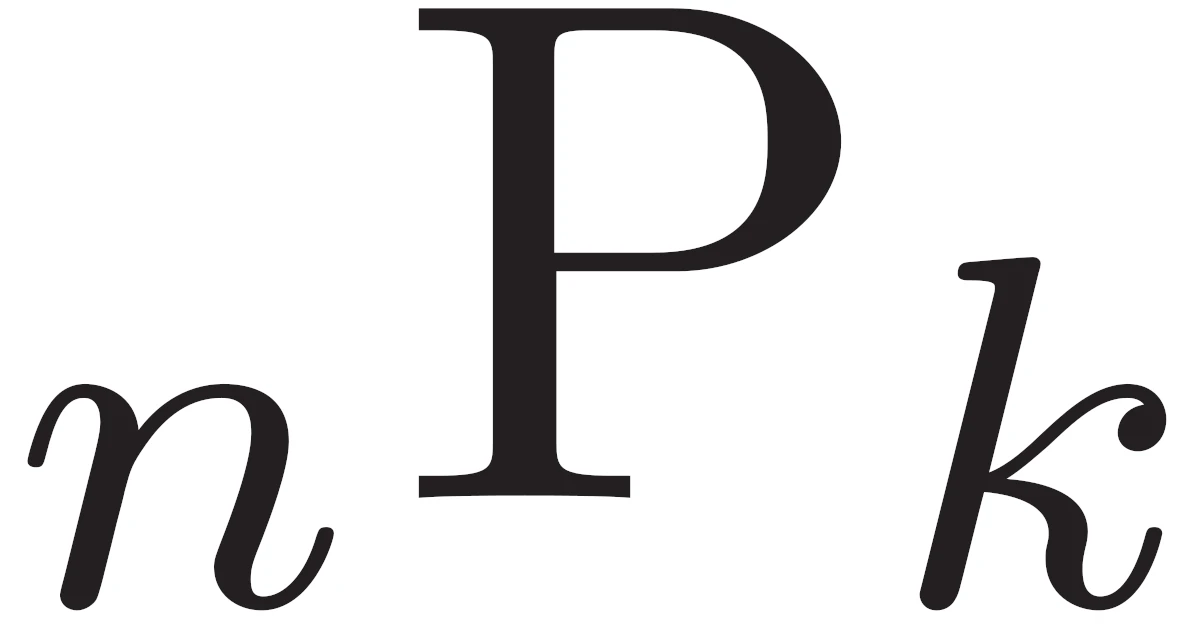
コメント