前回の記事では9枚のカード$\fbox{1}\fbox{2}\fbox{3}\dots\fbox{8}\fbox{9}$を「一列に」並べる場合の数を考えました.
このようにモノを並べることを順列といいましたが,この記事では一列に並べる基本的な順列ではなく「円状に」並べる円順列を考えます.
つまり,次のような問題を考えます.
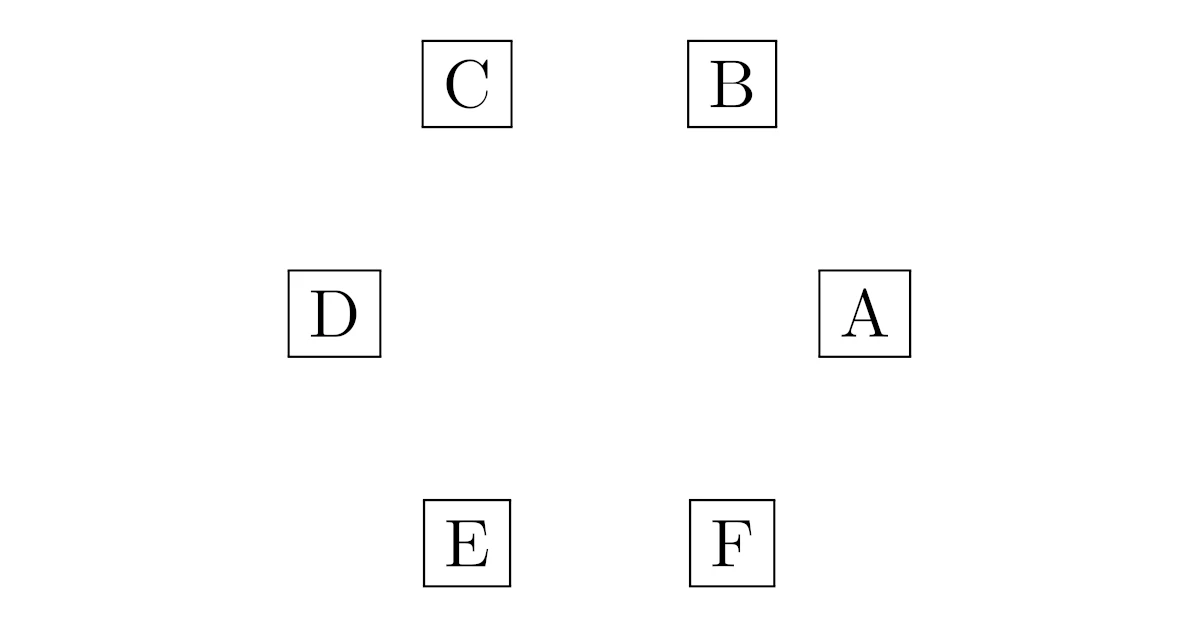
6枚のカード$\fbox{A}\fbox{B}\fbox{C}\fbox{D}\fbox{E}\fbox{F}$を円状に並べる場合の数を求めよ.
円状になると難しく感じるかもしれませんが,実は円順列の場合の数も簡単に求めることができます.
また,「円順列」と言った場合には裏返したものは別のものとみなしますが,裏返して同じになるものを同じとみなす順列を数珠順列といいます.
この記事では
- 円順列の考え方と公式
- 数珠順列の考え方と公式
を順に説明します.
「場合の数と確率」の一連の記事
円順列
次の問題のように,モノを円状に並べることを円順列といいます.
6枚のカード$\fbox{A}\fbox{B}\fbox{C}\fbox{D}\fbox{E}\fbox{F}$を円状に並べる場合の数を求めよ.ただし,回転して重なるものは同じとみなす.
なお,「回転して重なるものは同じとみなす」というのは,例えば
という並びのことですね.
一般に,「円順列」と言った場合には回転させて重なるものは同じものとみなします.
この問題を2つの考え方で解いてみましょう.
考え方1
考え方から丁寧に解きましょう.
6枚のカード$\fbox{A}\fbox{B}\fbox{C}\fbox{D}\fbox{E}\fbox{F}$を一列に並べる場合の数は$6!=720$より$720$通りである.
この$720$通りの順列それぞれについて,両端を繋げて円順列にする.例えば,順列$\fbox{A}\fbox{B}\fbox{C}\fbox{D}\fbox{E}\fbox{F}$は両橋の$\fbox{A}$と$\fbox{F}$を繋げて
と円順列にする.
この考え方によりできる,6つの円順列
- 順列$\fbox{A}\fbox{B}\fbox{C}\fbox{D}\fbox{E}\fbox{F}$を円順列にしたもの
- 順列$\fbox{B}\fbox{C}\fbox{D}\fbox{E}\fbox{F}\fbox{A}$を円順列にしたもの
- 順列$\fbox{C}\fbox{D}\fbox{E}\fbox{F}\fbox{A}\fbox{B}$を円順列にしたもの
- 順列$\fbox{D}\fbox{E}\fbox{F}\fbox{A}\fbox{B}\fbox{C}$を円順列にしたもの
- 順列$\fbox{E}\fbox{F}\fbox{A}\fbox{B}\fbox{C}\fbox{D}$を円順列にしたもの
- 順列$\fbox{F}\fbox{A}\fbox{B}\fbox{C}\fbox{D}\fbox{E}$を円順列にしたもの
を考えると,これらは全て同じものである.
同様に,$720$通りの順列それぞれを円順列にすると,6通りずつ同じ円順列ができあがる.
したがって,求める場合の数は$720\div6=120$より$120$通りである.
普通の順列を全て円順列にすると6個ずつ同じ円順列が出来上がるので,普通の順列の場合の数$720$を重複分の$6$で割れば答えが得られるという考え方ですね.
この「重複で割る」という考え方には最初は戸惑うかもしれませんが,慣れればとても使い勝手の良い考え方です.
考え方2
いまの考え方にピンとこない人は次のように考えてもいいでしょう.
最初にカード$\fbox{A}$を置き,残りの5ヶ所に残りの5枚を並べる.
最初に$\fbox{A}$を固定しているので,残りの5枚を並べると全て異なる順列となる.
よって,求める場合の数は5枚を並べる順列が求める場合の数だから,$5!=120$より$120$通りである.
先に$\fbox{A}$を固定してから円状に並べれば,回転して重なることはないので普通の順列と同じように考えられるというわけですね.
公式
いまの考え方と同じようにすれば,次の公式が得られます.
$n$個のものの円順列の場合の数は$(n-1)!$通りである.
1つ目の考え方をすれば,$n$個のものを一列に並べる場合の数は$n!$であり,これらを円状にすると$n$個ずつ重複するので,
となりますね.
また,2つ目の考え方をすれば,$n$個のうちの1つを固定して,残りの$(n-1)!$を並べるので$(n-1)!$通りとなりますね.
数珠順列
次に,数珠順列を考えましょう.
6枚のカード$\fbox{A}\fbox{B}\fbox{C}\fbox{D}\fbox{E}\fbox{F}$を円状に繋げる場合の数を求めよ.ただし,回転して重なるものと,裏返して重なるものは同じとみなす.
円順列は回転させて重なるものだけを同じとみなしましたが,加えて
のように裏返して重なるものも同じとみなす順列を数珠順列といいます.
数珠は繋がっているので,持ち上げて前から見たり後ろから見たりすることができます.前から見るのと後ろから見るのでは見た目は裏返っていますが同じ数珠ですね.
考え方
数珠順列は円順列をもとにして次のように求めることができます.
6枚のカード$\fbox{A}\fbox{B}\fbox{C}\fbox{D}\fbox{E}\fbox{F}$で円順列を考えると,円順列の公式から$(6-1)!=120$である.
この円順列のうち,
のように2通りずつ同じ円順列ができあがる.
したがって,求める場合の数は$120\div2=60$より$60$通りである.
先ほどの円順列の考え方1のように,円順列で考えてから重複分の$2$で割れば良いという考え方ですね.
公式
いまの考え方と同じようにすれば,次の公式が得られます.
$n$個のものの数珠順列の場合の数は$\dfrac{(n-1)!}{2}$である.
そもそも$n$個のものの円順列の場合の数は$(n-1)!$であり,この中に裏返して一致するものが2つずつあるので,重複分の$2$で割って
となりますね.
コメント