あまり意識されないことですが，「関数の極限」と「数列の極限」の違いが分かっていないと間違えてしまう問題もあります．
例えば
- 数列$a_n=\sin{\pi n}$
- 関数$f(x)=\sin{\pi x}$
としたとき，$\lim\limits_{n\to\infty}a_n$と$\lim\limits_{x\to\infty}f(x)$は異なる結果になりますが，関数の極限と数列の極限の違いが意識できていないと，間違えてしまうかもしれません．
この記事では
- 数列$a_n$の極限
- 関数$f(x)$の極限
の２つの違いを説明します．
一連の記事はこちら
【極限の基本１｜lim(リミット)の意味は？極限の考え方】
【極限の基本２｜「関数の極限」と「数列の極限」の２つの違い】←今の記事
【無限級数１｜[無限級数]の考え方を具体例から理解する】
【無限級数２｜無限級数の発散条件と収束しない３つの例】
【無限級数３｜無限等比級数の収束・発散は初項と公比に注目！】
解説動画
この記事の解説動画をYouTubeにアップロードしています．
この動画が良かった方は是非チャンネル登録をお願いします！
「関数の極限」と「数列の極限」の１つ目の違い
「関数の極限」と「数列の極限」の定義から１つ目の違いを説明します．
関数の極限
「関数の極限」には
- $x\to a$
- $x\to \pm\infty$
- $x\to a\pm0$
の３種類があります．
$x\to a$の極限
[関数の極限１] $x$が$a$と異なる値を取りながら$a$に限りなく近づくとき，関数$f(x)$がある一定の値$\alpha$に限りなく近付くならば，このことを
または
$x \to a$のとき$f(x)\to\alpha$
と表し，「$x\to a$のとき$f(x)$は$\alpha$に収束する」といい，この$\alpha$を「$x\to a$のときの$f(x)$の極限値」という．
この極限は微分を導入するために必要なので，数学IIで扱いますね．
この$x\to a$の極限については前回の記事で詳しく説明しています．
$x\to\pm\infty$の極限
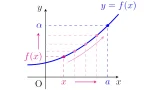
[関数の極限２] 正の$x$が限りなく大きくなるとき，関数$f(x)$がある一定の値$\alpha$に限りなく近付くならば，このことを
または
$x \to \infty$のとき$f(x)\to\alpha$
と表し，「$x\to \infty$のとき$f(x)$は$\alpha$に収束する」といい，この$\alpha$を「$x\to \infty$のときの$f(x)$の極限値」という．
[関数の極限２’] 負の$x$が限りなく小さくなるとき，関数$f(x)$がある一定の値$\alpha$に限りなく近付くならば，このことを
または
$x \to -\infty$のとき$f(x)\to\alpha$
と表し，「$x\to-\infty$のとき$f(x)$は$\alpha$に収束する」といい，この$\alpha$を「$x\to-\infty$のときの$f(x)$の極限値」という．
この極限は数学IIIの範囲です．
ある値に近付けるのではなく，限りなくどんどん$x$を大きくしたり，小さくしたりするのがこの極限です．
$x\to a\pm0$の極限
[関数の極限３] $x$が$a$より大きい値を取りながら$a$に限りなく近づくとき，関数$f(x)$がある一定の値$\alpha$に限りなく近付くならば，このことを
または
$x \to a+0$のとき$f(x)\to\alpha$
と表し，この$\alpha$を「$x\to a+0$のときの$f(x)$の右極限」という．
[関数の極限３’] $x$が$a$より小さい値を取りながら$a$に限りなく近づくとき，関数$f(x)$がある一定の値$\alpha$に限りなく近付くならば，このことを
または
$x \to a+0$のとき$f(x)\to\alpha$
と表し，この$\alpha$を「$x\to a+0$のときの$f(x)$の左極限」という．
この極限も数学IIIの範囲です．
なお，これらの定義で$a=0$の場合には
- 右極限は$x\to0+0$ではなく$x\to+0$
- 左極限は$x\to0-0$ではなく$x\to-0$
と表します．
例えば，$y=\dfrac{1}{x}$のグラフを描くと，以下のようになります．
この図から
- $x$を$0$に右から(大きい方から)近付けると，$\dfrac{1}{x}$はどんどん大きくなるので$\lim\limits_{x\to+0}\dfrac{1}{x}=\infty$
- $x$を$0$に左から(小さい方から)近付けると，$\dfrac{1}{x}$はどんどん小さくなるので$\lim\limits_{x\to+0}\dfrac{1}{x}=-\infty$
となります．
また，普通の極限$x\to a$は右極限$x\to a+0$と左極限$x\to a-0$が異なる場合には「存在しない」とするので，$\lim\limits_{x\to0}\dfrac{1}{x}$は存在しません．
数列の極限
一方，「数列の極限」は１種類しかありません．
[数列の極限] 数列$\{a_n\}$に対して，$n$を限りなく大きくするとき，$a_n$がある一定の値$\alpha$に限りなく近づくならば，
または
$n \to \infty$のとき$a_n\to\alpha$
と表し，「($n\to \infty$のとき)$\{a_n\}$は$\alpha$に収束する」といい，この$\alpha$を「($n\to \infty$のときの)$\{a_n\}$の極限値」という．
「数列の極限」では，「関数の極限」での$x \to a$に相当する極限はありません．
たとえば，関数では「$x\to3$」という極限を考えることがありますが，数列では「$n\to3$」という極限は考えません．
関数の極限の場合には
- $f(2.9)$
- $f(2.99)$
- $f(2.999)$
- $\dots$
のように$x$を$3$に近付けていくことで$x\to 3$の極限を考えることができますが，数列での$n$は整数なので$n=2,2.9,2.99,2.999,\dots$などとすることができません．
このため，関数の極限の$x\to a$と$x\to a\pm0$に相当するものが数列の極限にはなく，数列の極限は$n\to\infty$しか考えないわけですね．
「関数の極限」は$x\to a$，$x\to \pm\infty$，$x\to a\pm0$の３種類あるが，「数列の極限」は$n\to\infty$の１種類のみである．
「関数の極限」と「数列の極限」の２つ目の違い
２つ目の違いを見るために，次の問題を考えます．
次の問いに答えよ．
- 数列$a_n=\sin{\pi n}$について，極限$\lim\limits_{n\to\infty} a_n$が存在すれば求めよ．
- 関数$f(x)=\sin{\pi x}$について，極限$\lim\limits_{x\to\infty} f(x)$が存在すれば求めよ．
さて，どうでしょう．
冒頭でも書いたように，この２問の答えは異なります．
$a_n=\sin{\pi n}$と$f(x)=\sin{\pi x}$の違いは$n$と$x$の違いだけなので，「数列の$n$と関数の$x$がそれぞれ何者か」というところがポイントです．
数列の極限
まずは１問目です．$a_n=\sin{\pi n}$で定まる数列$\{a_n\}$は
- $a_1=\sin{\pi}=0$
- $a_2=\sin{2\pi}=0$
- $a_3=\sin{3\pi}=0$
- $\dots$
ですから，任意の自然数$n$に対して$a_n=0$です．よって，
となります．
関数の極限
次に２問目です．
$x$は実数なので，$f(x)=\sin{\pi x}$は$-1$から1の間を無限に往復し続けるので，$x\to\infty$としたときどこかに近づくということはありません．
したがって，$\lim\limits_{x\to\infty} f(x)$は存在しません．
このように，「関数の極限」と「数列の極限」の２つ目の違いは「数列の$n$は整数，関数の$x$は実数」です．
このように２問並べると違いに気付いて正しく答えられるかもしれませんが，どちらか１問を出されたときでも「数列の極限」なのか「関数の極限」なのかをしっかり意識して考えてください．
「関数の極限」では変数$x$は実数で，「数列の極限」では変数$n$は整数である．
無限級数
数列の分野では，$a_1+a_2+\dots+a_n$のような数列の和を考えました．
この数列の和は有限個の項の和ですが，数学IIIでは$a_1+a_2+\dots+a_n+\dots$のように無限に足し合わせ続けると，どんな値に近付くかを考えます．
この無限に足し合わせる数列の和は無限級数とよばれます．
次の記事では，無限級数の考え方を具体例を用いて説明します．