5枚のカード$\fbox{A}\fbox{B}\fbox{C}\fbox{D}\fbox{E}$から3枚選ぶ場合の数は,組み合わせの場合の数の考え方から$\Co{5}{3}$通りありますね.
では,次の問題はどうでしょうか?
2種類のカード$\fbox{A}\fbox{B}$から合わせて5枚選ぶ場合の数を求めよ.ただし,選ばれないものがあってもよいとする.
この問題は全て違うものからいくつか選ぶ普通の組み合わせとは異なり,何種類かのものから全部で何枚かを選ぶ組み合わせになっていますね.このような組み合わせを重複組み合わせといいます.
重複組合せの問題設定としては
- 選ばれない色のカードがあっても良い場合
- 選ばれないカードがあってはならない場合
の2パターンが考えられます.
最初はこれらを混同してしまうことが多いのですが,一方でこの2パターンさえしっかり区別して解けるようになれば,重複組み合わせは全く怖いものではありません.
この記事では
- 重複組み合わせの基本的な考え方
- 重複組み合わせの解法
- 重複組み合わせの公式
を順に説明します.この2パターンをどのように区別して考えるかを説明します.
「場合の数と確率」の一連の記事
重複組み合わせ
具体的な問題を考えながら,重複組み合わせの場合の数の求め方を考えていきましょう.
選ばれないものがあってもよい場合
まずは冒頭の問題を考えましょう.
2種類のカード$\fbox{A}\fbox{B}$から合わせて5枚選ぶ場合の数を求めよ.ただし,選ばれないものがあってもよいとする.
この問題を解くために,カードの選び方を次のように表しましょう.
「丸◯」5個と「仕切り|」1本を並べて
- |より左にある◯の個数でカード$\fbox{A}$の枚数
- |より右にある◯の個数でカード$\fbox{B}$の枚数
を表すものとします.例えば,
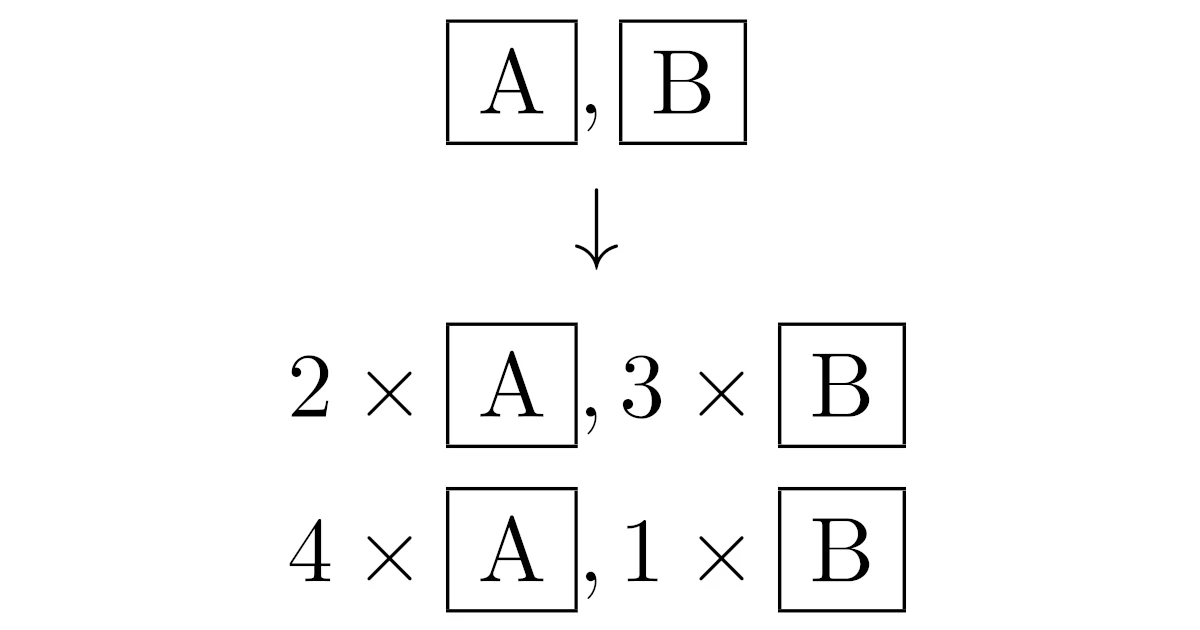
- ◯◯◯|◯◯ → $\fbox{A}$3枚,$\fbox{B}$2枚
- ◯|◯◯◯◯ → $\fbox{A}$1枚,$\fbox{B}$4枚
- ◯◯◯◯◯| → $\fbox{A}$5枚,$\fbox{B}$0枚
というわけですね.|が端にくれば,どちらかのカードは0枚を表すことに注意しましょう.
このように,カード$\fbox{A}\fbox{B}$の選び方は「丸◯」5個と「仕切り|」1本の並べ方と完全にピッタリ対応するわけですね.
この表し方を用いると,上の問題は次のように解けます.
「丸◯」5個と「仕切り|」1本の並べ方の総数は,求める場合の数に等しい.
この並べ方は◯5個,|1本の重複順列だから,求める場合の数は$\dfrac{6!}{5!1!}=6$である.
このように,◯と|の並べ方の問題に帰着させることで,あっさりと解けてしまうわけですね.
選ばれないものがあってはならない場合
次に,選ばれないものがあってはならないタイプの重複組み合わせの問題を考えましょう.
2種類のカード$\fbox{A}\fbox{B}$から合わせて5枚選ぶ場合の数を求めよ.ただし,選ばれないものがあってはならないとする.
この問題も同じように「丸◯」5個と「仕切り|」1本を並べて考えましょう.
先ほどの問題との違いは
- ◯◯◯◯◯| → $\fbox{A}$5枚,$\fbox{B}$0枚
- |◯◯◯◯◯ → $\fbox{A}$0枚,$\fbox{B}$5枚
が許されないだけですね.そこで,次のように解きましょう.
「丸◯」5個を先に並べておき,◯の隙間のどこかに「仕切り|」1本を差し込む場合の数は,求める場合の数に等しい.
◯の隙間は4ヶ所あるから,求める場合の数は$\Co{4}{1}=4$である.
このように,「最初から◯◯◯◯◯と5個並べておき,◯の隙間のどこかに|を差し込む」と考えれば,
- ◯◯◯◯◯|
- |◯◯◯◯◯
となることはないので,$\fbox{A}$も$\fbox{B}$も少なくとも1枚は選ばれていることになりますね.
具体例
今の問題では,2個以上同じものがあるのはカードが2種類だけでしたが,次のようになっても考え方は同じです.
3種類のカード$\fbox{A}\fbox{B}\fbox{C}$から合わせて6枚選ぶ.
- 選ばれないものがあってもよい場合の選び方の総数を求めよ.
- 選ばれないものがあってはならない場合の選び方の総数を求めよ.
今度は「丸◯」6個と「仕切り|」2本を並べて
- ◯◯◯|◯◯|◯ → $\fbox{A}$3枚,$\fbox{B}$2枚,$\fbox{C}$1枚
- ◯|◯|◯◯◯◯ → $\fbox{A}$1枚,$\fbox{B}$1枚,$\fbox{C}$4枚
- ◯◯◯◯◯||◯ → $\fbox{A}$5枚,$\fbox{B}$0枚,$\fbox{C}$1枚
と表すことを考えれば,次のように解けます.
(1) 「丸◯」6個と「仕切り|」2本の並べ方の総数は,求める場合の数に等しい.
この並べ方は◯6個,|2本の重複順列だから,求める場合の数は$\dfrac{8!}{6!2!}=28$である.
(2) 「丸◯」6個を先に並べておき,◯の隙間から2ヶ所選んで「仕切り|」2本を差し込む場合の数は,求める場合の数に等しい.
◯の隙間は5ヶ所あるから,求める場合の数は$\Co{5}{2}=10$である.
選ばれないものがあってもよい場合の$\dfrac{(n+r-1)!}{(n-1)!r!}$は${}_{n}H_{r}$と表すこともあります(が,組み合わせの考え方でも求まるので使う必要はありません).
重複組み合わせの公式
以上のように
- 選ばれないカードがあっても良い場合,例えば◯◯◯||◯◯◯◯◯◯という並びはアリ
- 選ばれないカードがあってはならない場合,例えば◯◯◯||◯◯◯◯◯◯という並びはナシ
という考え方の違いがあるため,選ばれないものがあってよい場合と選ばれないものがあってはいけない場合で考え方を変えなければならないわけですね.
さて,上の考え方と同様にして,次の公式が得られますね.
$n$種類のものから全部で$r$個選ぶ場合の数は
- 選ばれないものがあっても良い場合は$\dfrac{(r+n-1)!}{(n-1)!r!}$である.
- 選ばれないものがあってはならない場合は$\Co{r-1}{n-1}$
(1) 選ばれないものがあってもよい場合,「丸◯」$r$個と「仕切り|」$n-1$個による重複順列を考えれば良い.
よって,$\dfrac{(r+n-1)!}{r!(n-1)!}$が求める場合の数である.
(2) 選ばれないものがあってはならない場合,「丸◯」$r$個からできる$r-1$箇所の隙間に「仕切り|」$n-1$個を差し込む場所を選ぶ組み合わせを考えれば良い.
よって,$\Co{r-1}{n-1}$が求める場合の数である.
注意点は
- 「丸◯」を$n$種類に分けるために必要な「仕切り|」は$n-1$本である
- $r$個の「丸◯」の隙間は$r-1$個である
というところですね.
コメント