例えば,等比数列$\dfrac{1}{2},\ \dfrac{1}{4},\ \dfrac{1}{8}, \dfrac{1}{16},\dots$について,初項から順に項を
と無限に足し続けていくと,どんどん1に近付いていくことが分かります(このことはこの記事の中で説明します).
このように,数列$\{a_n\}$について初項から順に無限に和をとっていくときの付き先を$\{a_n\}$の無限級数といい,$\sum\limits_{n=1}^{\infty}a_n$で表します.
この記事では
- 数列の収束の復習
- 無限級数の定義と具体例
を順に説明します.
「極限」の一連の記事
数列の収束の復習
無限級数をきちんと定義するには数列の極限が必要なので,定義を確認しましょう.
数列$\{a_n\}$において,$n$を限りなく大きくするとき,$a_n$がある一定の値$\alpha$に限りなく近づくならば,
または
などと表し,数列$\{a_n\}$は$\alpha$に収束するといい,$\alpha$を数列$\{a_n\}$の極限値という.
また,数列$\{a_n\}$が収束しないとき,数列$\{a_n\}$は発散するという.
簡単な例をいくつか挙げると,
- $a_n=1+\frac{1}{n}$なら$\lim\limits_{n\to\infty}a_n=1$
- $a_n=n$なら$\lim\limits_{n\to\infty}a_n=\infty$
- $a_n=-n$なら$\lim\limits_{n\to\infty}a_n=-\infty$
- $a_n=(-1)^n$なら,数列$\{a_n\}$は振動する(発散する)
となりますね.
数列$\{a_n\}$が発散するが,正の無限大$\infty$にも負の無限大$-\infty$にも発散しないとき,$\{a_n\}$は振動するというのでした.
無限級数の定義と具体例
それでは,無限級数の説明に移ります.
無限級数の定義
一般項$a_n=\dfrac{1}{2^n}$の数列$\{a_n\}$を考えましょう.この数列は冒頭で考えた等比数列
ですね.この数列$\{a_n\}$の初項から第$n$項までの和を$S_n$としましょう.具体的に計算すると
- $S_1=\dfrac{1}{2}$
- $S_2=\dfrac{1}{2}+\dfrac{1}{4}=\dfrac{3}{4}$
- $S_3=\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}=\dfrac{7}{8}$
- ……
となりますね.このようにできた$S_1,S_2,S_3,\dots$は数の並びなので$\{S_n\}$も数列になっていますね.
この数列$\{S_n\}$で極限$n\to\infty$を考えたものは,初項から
と無限に項を足していったものと考えることができます.
まさにこの考え方が無限級数で,きちんと定義を書くと次のようになります.
数列$\{a_n\}$に対して,初項から第$n$項までの和
を考える.このときの数列$\{S_n\}$の極限を$\sum\limits_{k=1}^{\infty}a_k$と表し,数列$\{a_n\}$の無限級数という.
一般項が$a_n=\dfrac{1}{2^n}$の等比数列$\{a_n\}$の場合,無限級数
を$\sum\limits_{k=1}^{\infty}\dfrac{1}{2^k}$, $\lim\limits_{n\to\infty}\sum\limits_{k=1}^{n}\dfrac{1}{2^k}$などと表すわけですね.
あくまで無限級数は極限なので,
- 極限$\lim\limits_{n\to\infty}\sum\limits_{k=1}^{n}a_k$が存在するとき$\sum\limits_{k=1}^{\infty}a_k$は収束する
- 極限$\lim\limits_{n\to\infty}\sum\limits_{k=1}^{n}a_k$が存在しないとき$\sum\limits_{k=1}^{\infty}a_k$は発散する
といいます.また,無限級数$\sum\limits_{k=1}^{\infty}a_k$に対して,途中までの和$S_n=\sum\limits_{k=1}^{n}a_k$を部分和といいます.
収束する無限級数の具体例
結論から言えば,この級数は1となります.
のちの記事できちんと計算で求める方法を紹介しますが,ここでは直感的に図形の面積から求めてみましょう.
一辺の長さが1の正方形を用意すると,$a_1=\dfrac{1}{2}$は下図の色がついた部分の面積です.
さらに,$a_2=\dfrac{1}{4}$は下図の色がついた部分の面積です.
続いて,$a_3=\dfrac{1}{8}$は下図の色がついた部分の面積です.
このように1辺の長さが1の正方形を
と区切っていくと,この正方形の面積は$a_1+a_2+a_3+\dots$の極限であることが見てとれますね.
この正方形の面積は$1\times1=1$ですから,
となることが分かります.
普通の極限と同じく無限級数も「足し合わせたときに近付く値」をいうのであって,実際にその値になるとは限らないことに注意しましょう.
いまの問題の無限級数$\sum\limits_{k=1}^{\infty}\dfrac{1}{2^k}$も限りなく1に「近付いていく」のであって,いつか1になるわけではありません.
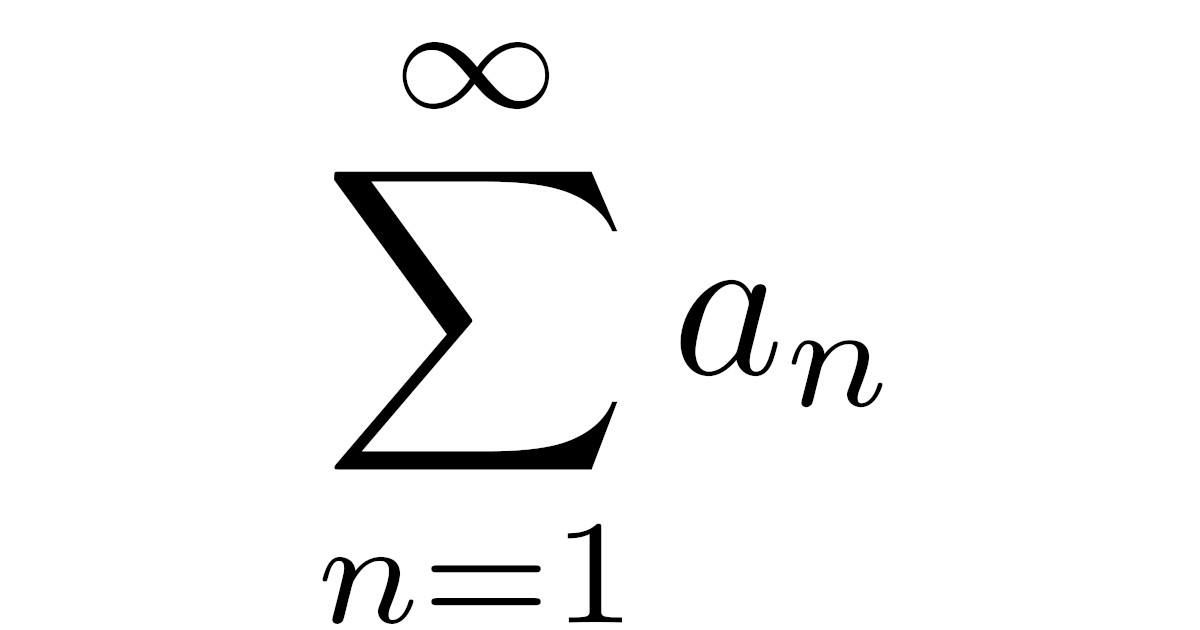
コメント