数列$\{a_n\}$の項を初項から順に
と無限に足していくとき,この和を$\sum\limits_{k=1}^{\infty}a_k$と表し,数列$\{a_n\}$の無限級数というのでした.
無限級数$\sum\limits_{k=1}^{\infty}a_k$のきちんとした定義は,初項から第$n$項までの和の極限$\lim\limits_{n\to\infty}(a_1+a_2+\dots+a_n)$でした.
前回の記事では無限級数の具体例として,一般項が$a_n=\dfrac{1}{2^n}$の数列の無限級数が
と$1$に収束することをみましたが,無限級数はいつでも収束するとは限りません.むしろ発散する無限級数はたくさんあります.
一般には無限級数の収束・発散の判定は簡単とは限りませんが,一発で発散することが判定できる無限級数もあります.
この記事では
- 無限級数の基本の発散条件
- 発散する無限級数の具体例
を順に説明します.
「極限」の一連の記事
無限級数と数列の収束・発散
無限級数の基本の発散条件の証明のためには次の定理が重要です.
無限級数が収束するときの数列の極限
数列$\{a_n\}$に対して,無限級数$\sum\limits_{k=1}^{\infty}a_k$が収束すれば,$\lim\limits_{n\to\infty}a_n=0$が成り立つ.
無限級数$\sum\limits_{k=1}^{\infty}a_k$の第$n$項までの部分和を$S_n$とする.すなわち,
とする.このとき,$a_{n}=S_{n}-S_{n-1}$であり,$S_{n}$, $S_{n-1}$はともに$\sum\limits_{k=1}^{\infty}a_k$に収束するから,
が成り立つ.よって,
が従う.
この証明でよく「$S_{n-1}$と$S_n$は同じとは限らないが,$\lim\limits_{n\to\infty}S_{n}=\lim\limits_{n\to\infty}S_{n-1}$となるのはなぜか?」という質問を受けます.
そもそも極限というのは「どこに近付くか」ということを表すものであって,「何になるか」ではないことが大切です.つまり,$\lim\limits_{n\to\infty}S_n$は「$n$を大きくしていくときの$S_n$の『近付き先』」という意味なわけですね.
いま無限級数$\sum\limits_{k=1}^{\infty}a_k$が収束することから,$S_n$も$S_{n-1}$も同じ値に近付くので$\lim\limits_{n\to\infty}S_{n}=\lim\limits_{n\to\infty}S_{n-1}$が成り立ちます.
無限級数の発散条件
この定理は対偶を考えて,次の形で用いることも多いです.
[無限級数の発散条件]0に収束しない数列$\{a_n\}$の無限級数$\sum\limits_{k=1}^{\infty}a_k$は発散する.
つまり,無限級数$\sum\limits_{k=1}^{\infty}a_k$をみたとき,数列$\{a_n\}$が0に収束していなければ,その瞬間に発散する無限級数であることが分かるわけですね.
$a_n$が$0$でないところを無限にさまよっていては,無限級数も収束しなさそうなことは直感的にも分かりますね.
無限級数が収束しない例
例1
一般項が$a_n=\dfrac{n}{n+1}$の数列$\{a_n\}$の無限級数$\sum\limits_{n=1}^{\infty}a_n$が発散することを示せ.
数列$\{a_n\}$の極限は
だから,数列$\{a_n\}$は$0$に収束しない.
よって,[無限級数の発散条件]から無限級数$\sum\limits_{k=1}^{\infty}a_k$は発散する.
十分大きい$n$に対しては$a_n\approx 1$ですから,この無限級数$\sum\limits_{k=1}^{\infty}a_k$はほとんど$1$の項を無限に足し続けることになります.
そう考えると確かにどこかの値に収束することはなさそうですね.
例2
一般項が$a_n=(-1)^n$の数列$\{a_n\}$の無限級数$\sum\limits_{n=1}^{\infty}a_n$が発散することを示せ.
問題の数列$\{a_n\}$は
- $n$が奇数のとき$a_n=-1$
- $n$が偶数のとき$a_n=1$
だから,数列$\{a_n\}$は$0$に収束しない.
よって,[無限級数の発散条件]から無限級数$\sum\limits_{k=1}^{\infty}a_k$は発散する.
実際に$a_n=(-1)^n$の初項から第$n$項までの部分和$S_n$を考えると,
- $S_1=a_1=-1$
- $S_2=a_1+a_2=0$
- $S_3=a_1+a_2+a_3=-1$
- $S_4=a_1+a_2+a_3+a_4=0$
- ……
と$0$と$-1$を往復することが分かります.詳しく書けば,
- $n$が偶数のとき,$S_n=-1+1-\dots+1=0$
- $n$が奇数のとき,$S_n=-1+1-\dots-1=-1$
と部分和$S_n$は$0$と$-1$の間を行き来するので,無限級数$\sum\limits_{k=1}^{n}a_k$は振動するということになります.
確かに無限級数$\sum\limits_{k=1}^{n}a_k$が発散していることが分かりましたね.
例3
一般項が$a_n=\dfrac{1}{n}$の数列$\{a_n\}$の無限級数$\sum\limits_{n=1}^{\infty}a_n$が発散することを示せ.
この問題の$a_n$の極限がどうなるかを考えると
となっています.したがって,この問題では[無限級数の発散条件]を適用することはできません.
しかし,次のように発散することが証明できます.
任意の$k=1,2,\dots$に対して,$a_{2^k+1}$から$a_{2^{k+1}}$をまとめて足し合わせると
と発散することが分かる.
つまり,任意の$k=1,2,\dots$に対して
となることを用いているわけですね.
積分を用いても発散することは証明できます(数学IIIの重要な基本問題です)が,少しテーマが変わるのでここでは省略します.
ここで「$\lim_{n\to\infty}a_n=0$なのに発散するのは[無限級数の発散条件]と矛盾してない?」と思う方もいらっしゃるかもしれません.
結論から言えば矛盾していません.もう一度[無限級数の発散条件]を確認してみましょう.
[無限級数の発散条件(再掲)]0に収束しない数列$\{a_n\}$の無限級数$\sum\limits_{k=1}^{\infty}a_k$は発散する.
[無限級数の発散条件]は$\lim\limits_{n\to\infty}a_n\neq0$のときの話であって,$\lim\limits_{n\to\infty} a_n=0$のときに無限級数$\sum\limits_{k=1}^{\infty}a_k$の発散・収束については何も言っていないということに注意してください.
そして,この例3の数列$\{a_n\}$は「$\lim\limits_{n\to\infty}a_n=0$を満たすが,無限級数$\sum\limits_{k=1}^{\infty}a_k$が収束しない例」になっているわけですね.
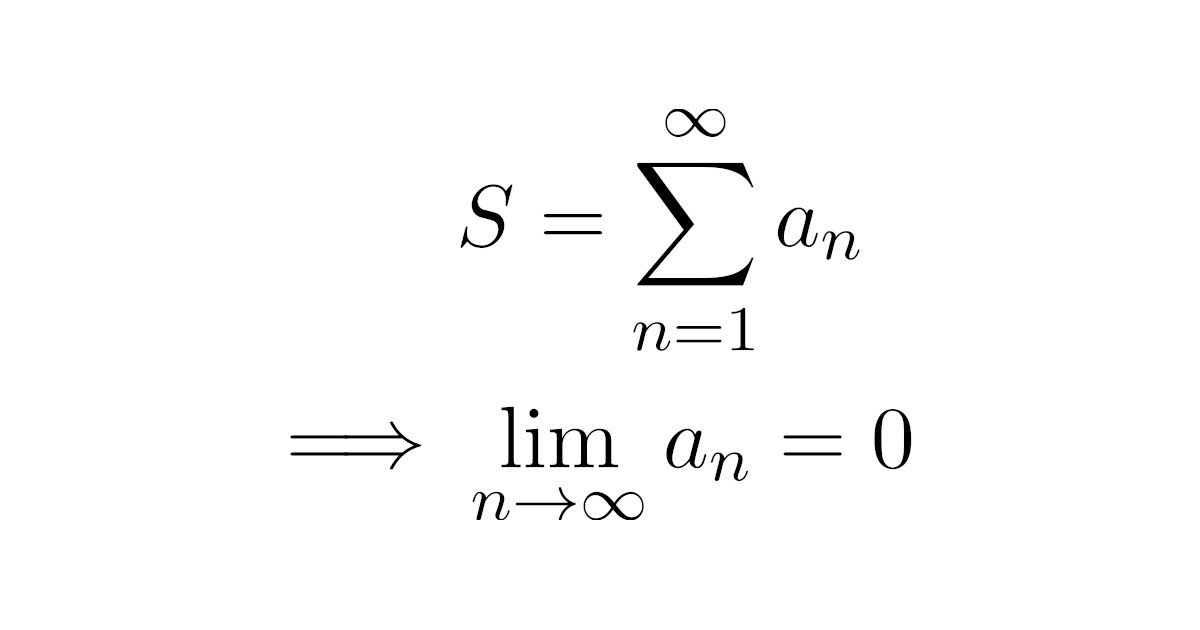
コメント