例えば,次の問題を考えましょう.
$\sin{75^\circ}$, $\cos{105^\circ}$, $\tan{-15^\circ}$を求めよ.
$75^\circ$も$105^\circ$も$-15^\circ$もいわゆる有名角ではないので,すぐには求めることができません.
しかし,この記事で説明する三角関数の加法定理を用いることで,これらを求めることができます.
この記事では
- 加法定理とはどんな公式か?
- 加法定理の使い方の具体例
- 加法定理の証明
を順に説明します.
「三角関数」の一連の記事
加法定理
加法定理は偏角が和$\alpha+\beta$または差$\alpha-\beta$になっているときに使える公式です.
[加法定理] 実数$\alpha$, $\beta$に対して,以下が成り立つ.
ただし,
- $\tan{(\alpha+\beta)}$の加法定理では$\cos{\alpha}\neq0$, $\cos{\beta}\neq0$, $\cos{(\alpha+\beta)}\neq0$
- $\tan{(\alpha-\beta)}$の加法定理では$\cos{\alpha}\neq0$, $\cos{\beta}\neq0$, $\cos{(\alpha-\beta)}\neq0$
とする.
最後の$\tan$の条件は,$\tan$が$\cos{\theta}\neq0$のときに$\tan{\theta}=\dfrac{\sin{\theta}}{\cos{\theta}}$と定義されるからですね.
証明は後回しにして,これらの使い方を具体例から考えましょう.
加法定理の具体例
加法定理を用いて,この記事の冒頭の問題を解いてみましょう.
次の値を求めよ.
- $\sin{75^\circ}$
- $\cos{105^\circ}$
- $\tan{-15^\circ}$
加法定理を意識すると,$75^\circ$, $105^\circ$, $-15^\circ$を有名角$\alpha$, $\beta$の差で表したいところです.
例えば,
- $75^\circ=30^\circ+45^\circ$
- $105^\circ=45^\circ+60^\circ$
- $-15^\circ=30^\circ-45^\circ$
とみれば,加法定理から次のように求めることができます.
(1)加法定理$\sin{(\alpha+\beta)}=\sin{\alpha}\cos{\beta}+\cos{\alpha}\sin{\beta}$で$\alpha=30^\circ$, $\beta=45^\circ$とみれば,
となる.
(2)加法定理$\cos{(\alpha-\beta)}=\cos{\alpha}\cos{\beta}+\sin{\beta}\sin{\alpha}$で$\alpha=45^\circ$, $\beta=60^\circ$とみれば,
となる.
(3)加法定理$\tan{(\alpha-\beta)}=\dfrac{\tan{\alpha}-\tan{\beta}}{1+\tan{\alpha}\tan{\beta}}$で$\alpha=30^\circ$, $\beta=45^\circ$とみれば,
である.
和の表し方は1通りではありません.例えば$105^\circ=135^\circ-30^\circ$とみても,$\cos{105^\circ}$は
と(当然ながら)同じ結果になりますね.
加法定理と偏角の変換公式
以前の記事で説明した偏角の変換公式は加法定理から導出することもできます.
実数$\theta$に対して,
- $\cos{(-180^{\circ}-\theta)}$
- $\sin{(\theta-90^{\circ})}$
- $\tan{(180^{\circ}-\theta)}$
を$\sin{\theta}$, $\cos{\theta}$, $\tan{\theta}$を用いて表せ.
(1)加法定理$\cos{(\alpha-\beta)}=\cos{\alpha}\cos{\beta}+\sin{\beta}\sin{\alpha}$で$\alpha=-180^\circ$, $\beta=\theta$とみれば,
ですね.
(2)加法定理$\sin{(\alpha-\beta)}=\sin{\alpha}\cos{\beta}-\cos{\alpha}\sin{\beta}$で$\alpha=\theta$, $\beta=90^\circ$とみれば,
ですね.
(3)加法定理$\tan{(\alpha-\beta)}=\dfrac{\tan{\alpha}-\tan{\beta}}{1+\tan{\alpha}\tan{\beta}}$で$\alpha=180^\circ$, $\beta=\theta$とみれば,
ですね.
ただし,以前に説明したように図を見れば瞬時に導ける基本的な
- $(\theta\pm180^{\circ})$型の公式
- $(-\theta)$型の公式
- $(90^{\circ}-\theta)$型の公式
は当たり前にしておくのが良いでしょう.
加法定理の証明
それでは6つの公式を証明していきますが,まずは$\cos{(\alpha+\beta)}$の加法定理を証明します.
この$\cos{(\alpha+\beta)}$の加法定理から,他の加法定理を芋づる式に導くことができます.
他にもベクトルの内積を用いれば,最初に$\cos{(\alpha-\beta)}$を示すこともできます.
$\cos{(\alpha+\beta)}$の加法定理の証明
(再掲)実数$\alpha$, $\beta$に対して
が成り立つ.
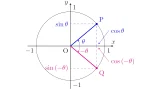
$xy$平面の単位円上に,4点
- 偏角$0$の点$\mrm{P}$
- 偏角$\alpha+\beta$の点$\mrm{Q}$
- 偏角$\alpha$の点$\mrm{A}$
- 偏角$\beta$の点$\mrm{B}$
をとる.
このとき,4点の座標は
- $\mrm{P}(1,0)$
- $\mrm{Q}(\cos{(\alpha+\beta)},\sin{(\alpha+\beta)})$
- $\mrm{A}(\cos{(-\alpha)},\sin{(-\alpha)})$
- $\mrm{B}(\cos{\beta},\sin{\beta})$
であり,線分$\mrm{PQ}$を原点中心に偏角$-\alpha$だけ回転させると線分$\mrm{AB}$に一致するから,$\mrm{PQ}=\mrm{AB}$が従う.
なので,
が従う.
$\cos(\alpha-\beta)$の加法定理の証明
(再掲)実数$\alpha$, $\beta$に対して
が成り立つ.
$\cos{(\alpha+\beta)}$の加法定理で,$\beta$の代わりに$-\beta$を用いれば,
が成り立ちますね.
なお,最後の等号で$(-\theta)$型の偏角の変換公式を用いています.
$\sin(\alpha-\beta)$の加法定理の証明
(再掲)実数$\alpha$, $\beta$に対して
が成り立つ.
$(90^\circ-\theta)$型の偏角の変換公式より
ですね.ここで,$\cos{(\alpha+\beta)}$の加法定理で,$\alpha$の代わりに$90^\circ-\alpha$を用いれば,
が成り立ちます.
なお,最後の等号で$(90^\circ-\theta)$型の偏角の変換公式を用いています.
$\sin(\alpha+\beta)$の加法定理の証明
(再掲)実数$\alpha$, $\beta$に対して
が成り立つ.
$\sin{(\alpha-\beta)}$の加法定理で,$\beta$の代わりに$-\beta$を用いれば,
このとき
が成り立ちます.
なお,最後の等号で$(-\theta)$型の偏角の変換公式を用いています.
$\tan(\alpha+\beta)$の加法定理の証明
(再掲)実数$\alpha$, $\beta$に対して
が成り立つ.
$\cos{\theta}\neq0$なる任意の実数$\theta$に対して$\tan{\theta}=\dfrac{\sin{\theta}}{\cos{\theta}}$と定義されるので,
が成り立ちます.
なお,2つ目の等号では$\cos(\alpha+\beta)$, $\sin(\alpha+\beta)$の加法定理を用いており,2つ目の等号では分母分子を$\cos{\alpha}\cos{\beta}$で割っています.
$\tan(\alpha-\beta)$の加法定理の証明
(再掲)実数$\alpha$, $\beta$に対して
が成り立つ.
$\tan{(\alpha+\beta)}$の加法定理で,$\beta$の代わりに$-\beta$を用いれば,
が成り立ちます.
なお,最後の等号で$(-\theta)$型の偏角の変換公式を用いています.
コメント