小学校以来，私たちは$30^\circ$のように「〜度」という単位で角度の大きさを表してきました．
この「〜度」という角度の大きさの表し方を度数法といいますが，度数法は数学的にはあまり都合の良い角度の表し方ではありません．
一方，より数学的に扱いやすい角度の大きさの表し方として弧度法があります．
弧度法は度数法よりも都合が良いことが多く，弧度法を使えば「扇型の面積」などの計算も簡単にできます．
この記事では，
- 弧度法の定義と具体例
- 弧度法に関する基本公式
を順に説明します．
「三角関数」の一連の記事
弧度法の定義と具体例
名前の通り，弧度法は円の「弧」をもとに定義されます．
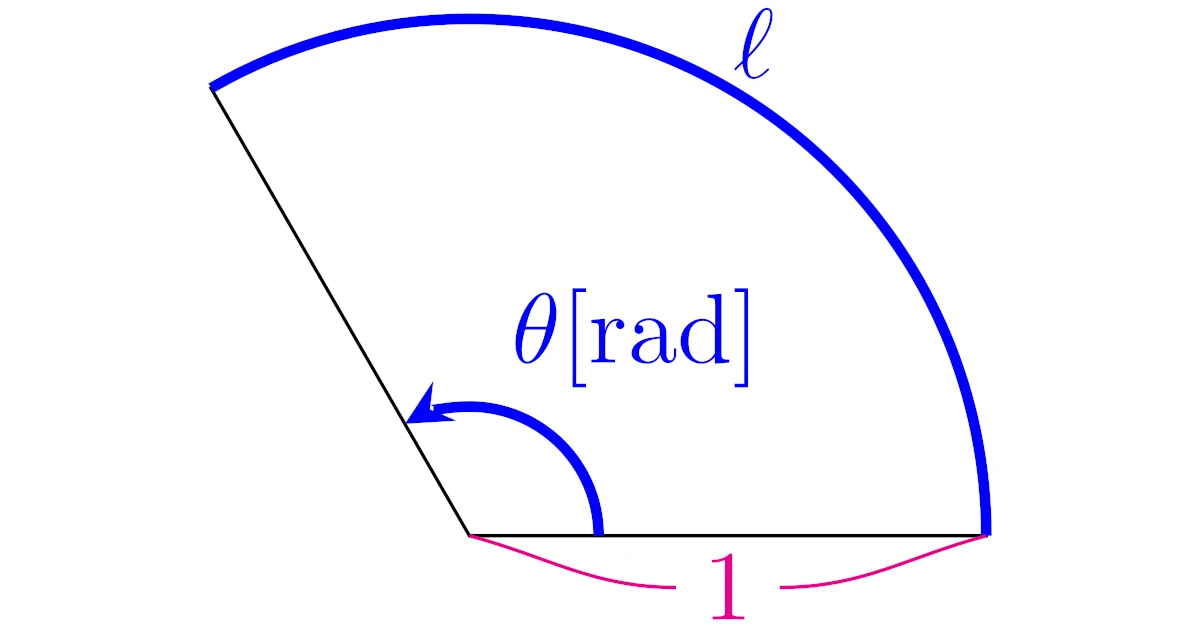
半径１の扇形の弧の長さが$\theta$であるとき，この扇形の中心角の大きさを$\theta[\mrm{rad}]$と定める．ただし，$\mrm{rad}$は「ラジアン（radian）」と読む．
この角度の大きさの表し方を弧度法という．
この定義から，半径$1$の円においては，
- 中心角が$\theta[\mrm{rad}]$
- 弧の長さが$\theta$
はどちらも同じ意味であることになりますね．
また，「弧度法」においては，単位の$[\mrm{rad}]$を省略することが多いです．
つまり，「中心角$\theta[\mrm{rad}]$」というのと「中心角$\theta$」というのは，同じことを意味します．
具体例１
半径１，中心角が$\dfrac{5\pi}{6}$の扇形のこの長さを$\ell$としましょう．
半径１の扇形においては(中心角)=(弧の長さ)なので，上図の扇形の弧の長さ$\ell$は
となりますね．
具体例２
半径２，中心角が$\dfrac{\pi}{3}$の扇形のこの長さを$\ell$としましょう．
半径１の扇形においては(中心角)=(弧の長さ)でしたが，半径が２になれば相似を考えて弧の長さも２倍になります．
ですから，上図の扇形の弧の長さ$\ell$は
となりますね．
度数法と弧度法の関係
度数法と弧度法の関係は下表のようになります．
| 度数法 | $0^\circ$ | $30^\circ$ | $45^\circ$ | $60^\circ$ | $90^\circ$ | $120^\circ$ | $135^\circ$ | $150^\circ$ | $180^\circ$ |
|---|---|---|---|---|---|---|---|---|---|
| 弧度法 | 0 | $\dfrac{\pi}{6}$ | $\dfrac{\pi}{4}$ | $\dfrac{\pi}{3}$ | $\dfrac{\pi}{2}$ | $\dfrac{2\pi}{3}$ | $\dfrac{3\pi}{4}$ | $\dfrac{5\pi}{6}$ | $\pi$ |
コツとして度数法での$180^\circ$と弧度法での$\pi$が一致することを意識しておけば，
- ６等分すれば$30^\circ$は$\dfrac{\pi}{6}$に等しい
- ４等分すれば$45^\circ$は$\dfrac{\pi}{4}$に等しい
- ３等分すれば$60^\circ$は$\dfrac{\pi}{3}$に等しい
となることはすぐに分かりますね．また，２倍すれば$360^\circ$は$2\pi$に等しいことも分かりますね．
弧度法の基本公式
弧度法について，次の弧の長さの公式と面積の公式の公式は当たり前にしておきましょう．
弧の長さの公式
半径$r$，中心角$\theta$の扇形について，弧の長さ$\ell$は
で得られる．
半径１，中心角$\theta$の扇形Aと半径$r$，中心角$\theta$の扇形Bは相似で相似比は$1:r$である．
よって，$1:r=\theta:\ell\iff\ell=r\theta$を得る．
上の例２でも同じ考えで弧の長さを求めましたね．
面積の公式
半径$r$，中心角$\theta$の扇形について，面積$S$は
で得られる．
一般に，半径$r$，弧の長さ$\ell$の扇形の面積は$\dfrac{1}{2}r\ell$であることに注意する．
上で示した公式から半径$r$，中心角$\theta$の扇形の弧の長さは$r\theta$だから，面積$S$は
である．
コメント