前回の記事で説明した三角関数のグラフは$\sin{\theta}$, $\cos{\theta}$の定義と$\tan{\theta}$の性質を踏まえれば簡単に得られるのでした.
さて,この記事では
- $\tan{\theta}=-1$ $(0\leqq\theta<2\pi)$
- $\cos{(\theta+\pi)}>\dfrac{\sqrt{2}}{2}$ $(0<\theta\leqq\pi)$
のような三角関数に関する方程式・不等式を考えますが,これらも$\sin{\theta}$, $\cos{\theta}$の定義と$\tan{\theta}$の性質を理解していれば簡単に解くことができます.
この記事では
- 三角関数の方程式
- 三角関数の不等式
の解き方を具体例をから説明します.
「三角関数」の一連の記事
三角関数の基本の確認
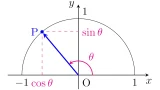
この記事を通して,偏角$\theta$の単位円周上の点を$\mrm{P}$とします.
$\cos{\theta}$, $\sin{\theta}$の性質
このとき,
- 点$\mrm{P}$の$x$座標を$\cos{\theta}$
- 点$\mrm{P}$の$y$座標を$\sin{\theta}$
と定義するのでしたね.
$\tan{\theta}$の図形的性質
また,$xy$平面上の直線$x=1$と直線$\mrm{OP}$の交点の$y$座標が$\tan\theta$となるのでした.
この記事の方程式・不等式はこれらをふまえながら解いていきます.
なお,これら三角関数の定義については以下の記事を参照してください.
三角関数の方程式
次の$\theta$の方程式を解きましょう.
- $\sin{\theta}=\dfrac{1}{2}$ $(0\leqq\theta\leqq\pi)$
- $2\cos{\theta}=1$ $\bra{-\dfrac{\pi}{2}<\theta<\dfrac{\pi}{2}}$
- $\sqrt{3}\tan{\theta}=-1$ $(0\leqq\theta<2\pi)$
これらの方程式では,最初に未知数の範囲に注目して,単位円上の点を点$\mrm{P}$がどの部分を動くかを意識しましょう.
問1
$\theta$の方程式$\sin{\theta}=\dfrac{1}{2}$ $(0\leqq\theta\leqq\pi)$を解け.
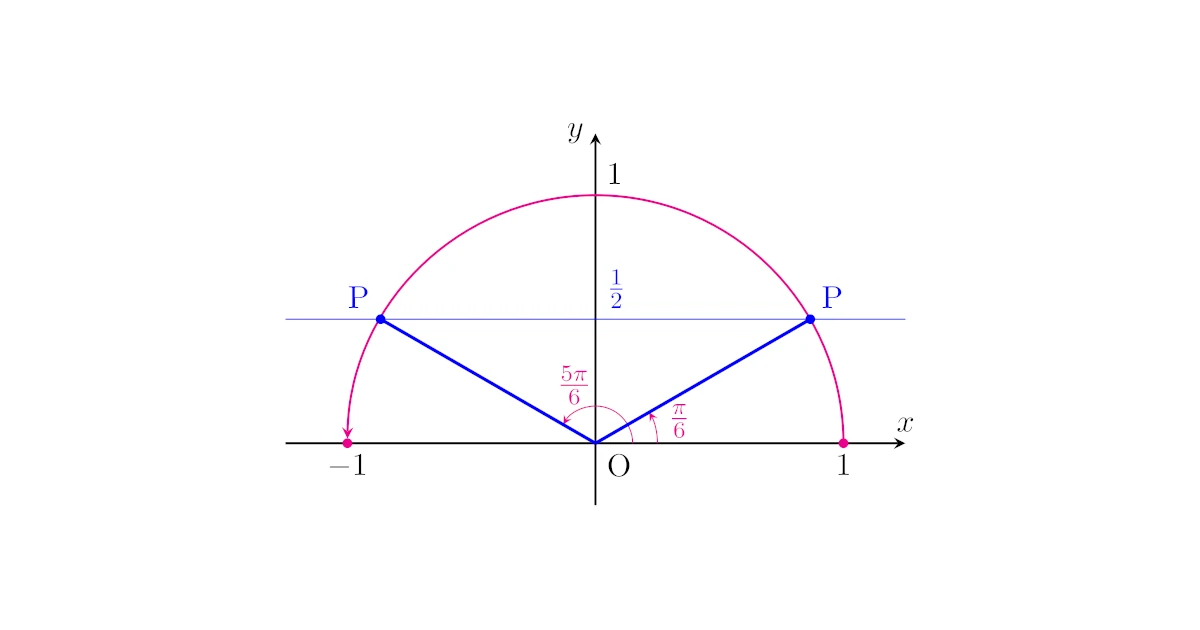
$0\leqq\theta\leqq\pi$のとき,単位円周上の偏角$\theta$の点$\mrm{P}$は下図の半円上を動きます.
また,$\sin{\theta}=\dfrac{1}{2}$は点$\mrm{P}$の$y$座標が$\dfrac{1}{2}$となるということですから,
と解けますね.
問2
$\theta$の方程式$2\cos{\theta}=1$ $\bra{-\dfrac{\pi}{2}<\theta<\dfrac{\pi}{2}}$を解け.
方程式の両辺を$2$で割って,$\cos{\theta}=\dfrac{1}{2}$ $\bra{-\dfrac{\pi}{2}\leqq\theta\leqq\dfrac{\pi}{2}}$を解けばいいですね.
$-\dfrac{\pi}{2}\leqq\theta\leqq\dfrac{\pi}{2}$のとき,単位円周上の偏角$\theta$の点$\mrm{P}$は下図の半円上を動きます.
また,$\cos{\theta}=\dfrac{1}{2}$は点$\mrm{P}$の$x$座標が$\dfrac{1}{2}$となるということですから,
と解けますね.
問3
$\theta$の方程式$\sqrt{3}\tan{\theta}=-1$ $(0\leqq\theta<2\pi)$を解け.
方程式の両辺を$\sqrt{3}$で割って,$\tan{\theta}=-\dfrac{1}{\sqrt{3}}$ $(0\leqq\theta<2\pi)$を解けばいいですね.
$0\leqq\theta<2\pi$のとき,単位円周上の偏角$\theta$の点$\mrm{P}$は下図の円周上を動きます.
また,$\tan{\theta}=-\dfrac{1}{\sqrt{3}}$は直線$\mrm{OP}$と直線$x=1$の交点の$y$座標が$-\dfrac{1}{\sqrt{3}}$となるということですから,
と解けますね.
三角関数の不等式
以上の方程式の考え方と同様にすれば不等式も解くことができるので,偏角が$\theta$ではない不等式の解き方を説明します.
$\theta$の不等式$2\cos{(\theta+\pi)}>-\sqrt{2}$ $(0<\theta\leqq\pi)$を解け.
$\varphi=\theta+\pi$とおくと不等式は
となり,$0<\theta\leqq\pi$に注意すると$\varphi$は$\pi<\varphi\leqq2\pi$を動きます.
よって,まずは$\cos{\varphi}>-\dfrac{\sqrt{2}}{2}$ $(\pi<\varphi\leqq2\pi)$を解いてから,得られた$\varphi$の範囲と$\varphi=\theta+\pi$を併せて$\theta$を求めればいいですね.
$\pi<\varphi\leqq2\pi$のとき,単位円周上の偏角$\varphi$の点$\mrm{Q}$は下図の半円上を動きます.
また,$\cos{\varphi}>-\dfrac{\sqrt{2}}{2}$はは点$\mrm{Q}$の$x$座標が$-\dfrac{\sqrt{2}}{2}$より大きいということですから,
と解けますね.
もともと$\varphi=\theta+\pi$とおいていたので,解は
となりますね.
コメント