数学における集合はざっくり言えば「モノの集まり」のことを言います.
高校数学の中では集合の重要さが分かりにくく,残念ながらあまり目立たない分野となっていますが,集合は数学の最も基礎的な概念なので基本的な扱い方はマスターしておきたいところです.
この記事では,集合の基礎として
- 集合の定義
- 集合の2種類の表し方
- 2つの集合の関係
を順に説明します.
「論理と集合」の一連の記事
集合の定義
まず集合にどんなものがあるのかを考えて,集合をどのように表すかを解説します.
集合の具体例
高校数学において,集合は以下のように考えます.
数学的な対象の集まりを集合という.
たとえば,
- $3$以上$10$以下の整数全部の集合
- $6$の正の約数全部の集合
- 正多角形全部の集合
など集合には様々なものが考えられます.
集合の要素
例えば,「6の正の約数全部の集合」は1,2,3,6からできていますね.
この「6の正の約数全部の集合」に対する$1,2,3,6$のように,集合を構成する対象について次のように言います.
集合を構成する1つ1つの対象を要素(または元)という.
また,集合$A$が要素$a$をもつとき,$a$は$A$に属するといい$a\in A$と表す.また,$b$が$A$に属さないときは$b\not\in A$と表す.
つまり,「6の正の約数の集合」を$A$とすると,$A$の要素は1,2,3,6で,例えば$1\in A$や$3\in A$と表すわけですね.
一方,5のように集合$A$に属さない要素は$5\not\in A$と表すわけですね.
集合の2種類の表し方
集合の表し方は
- 要素を書き並べて表す方法
- 要素の性質によって表す方法
の2種類があります.
集合の表し方1
例えば,6の正の約数の集合$A$の要素は1,2,3,6なので,集合$A$はこれらを$\{\quad\}$で囲んで
と表します.
このように集合に属する全ての要素を$\{\quad\}$で囲んで表すのがひとつ目の集合の表し方です.
集合の表し方2
一方,集合に属する要素の性質によって表す方法もあります.例えば,$6$の正の約数の集合$A$は
$\{n|n$は6の正の約数$\}$
と表します.もう少し詳しく説明すると
- 前の“$\{n|$”の部分は「この集合は$n$全部の集合である」
- 後ろの“|$n$は6の正の約数$\}$”の部分で「$n$は6の正の約数である」
という意味の表し方になっています.
「集合の表し方1」のように要素を書き並べて表す方法を外延的記法といい,「集合の表し方2」のように要素の性質で集合を表す方法を内包的記法といいますが,これらの名前も覚える必要はありません.
具体例1(3以上10以下の整数全部の集合)
3以上10以下の整数全部の集合$A$を,要素を並べて表す方法と要素の性質で表す方法の2通りで表せ.
3以上10以下の整数全部の集合$A$は
- $A=\{3,4,5,6,7,8,9,10\}$
- $A=\{n|nは正の整数\ かつ\ 3\leqq n\leqq10\}$
と表せる.
具体例2(100以下の負でない偶数全部の集合)
100以下の負でない偶数全部の集合$A$を,要素を並べて表す方法と要素の性質で表す方法の2通りで表せ.
100以下の負でない偶数全部の集合$A$は
- $A=\{0,2,4,6,\dots,98,100\}$
- $A=\{n|nは負でない偶数\ かつ\ n\leqq100\}$
と表せる.
性質を用いて表す方法(内包的記法)による表し方はさまざま考えられ,例えば$A=\{n|0\leqq n\leqq100$かつ$n$は偶数$\}$と表すこともできます.
具体例3(−2以上1未満の実数全部の集合)
網羅的に要素を書き並べて表すのが難しいこともあります.
−2以上1未満の実数全部の集合$I$を,要素の性質で表す方法で表せ.
−2以上1以下の実数全部の集合$I$は
と表せる.
この問題の集合$I$は数直線上にべったりと張り付いている集合なので,要素を網羅的に書き並べるのが難しい例になっています.
要素を書き並べて表す方法はどのような要素が属しているか分かり易いのですが,このように書き表すのが難しいことも少なくありません.
このようなときのために,要素の性質で表す方法にも慣れておきましょう.
2つの集合の関係
最後に,2つの集合の関係について
- 部分集合
- 集合の相等
を説明します.
部分集合
集合が2つあるとき,一方が他方にすっぽり含まれている場合があります.このようなときは次のようにいいます.
集合$A$の要素が全て集合$B$の要素でもあるとき,$A$を$B$の部分集合(または$B$は$A$を含む)といい$A\subset B$と表す.また,$A$が$B$の部分集合でないとき,$A\not\subset B$と書く.
たとえば,
- $A=\{\dots,-12,-6,0,6,12,\dots\}$($6$の倍数の集合)
- $B=\{\dots,-6,-3,0,3,6,\dots\}$($3$の倍数の集合)
とするとき,$A$の要素は全て$B$の要素なので$A\subset B$となります.
集合$A$の要素が全て集合$A$の要素ですから,どんな集合$A$に対しても$A\subset A$はいつでも成り立つことに注意しましょう.
つまり,記号$\subset$はすっぽり含まれていることを意味するような形をしていますが,同じ集合であっても$\subset$を用いるわけですね.
集合の相等
このことに注意して,次のように「集合が等しい」ということを定義します.
集合$A$, $B$が$A\subset B$かつ$B\subset A$を満たすとき,$A$, $B$は等しいといい$A=B$と表す.
例えば,次のようになりますね.
集合$A$, $B$を
- $A=\{n|nは2の倍数かつ3の倍数\}$
- $B=\{n|nは6の倍数\}$
で定めるとき,$A=B$であることを示せ.
きちんと定義に従って,$A\subset B$かつ$B\subset A$を示せば良いですね.
[1]$A\subset B$を示す.このためには,$A$の要素が全て$B$に属していることを示せばよい.
$A$の任意の要素$n$は2の倍数だから,$n=2k$ ($k$は整数)と表すことができる.
ここで,もし$k$が3の倍数でなければ$n$は3の倍数になり得ないから,$k$は3の倍数である.よって,$k=3\ell$($\ell$は整数)と表すことができる.
これより$n=6\ell$となり$n$は6の倍数だから$B$に属する.これで$A\subset B$が示された.
[2]$B\subset A$を示す.このためには,$B$の要素が全て$A$に属していることを示せばよい.
$B$の任意の要素$n$は6の倍数だから,$n=6k$ ($k$は整数)と表すことができる.
よって,$n=2\times 3k$だから$n$は2の倍数であり,$n=3\times 2k$だから$n$は3の倍数である.
これより$n$は$A$に属するから,これで$A\subset B$が示された.
[1][2]より$A=B$が従う.
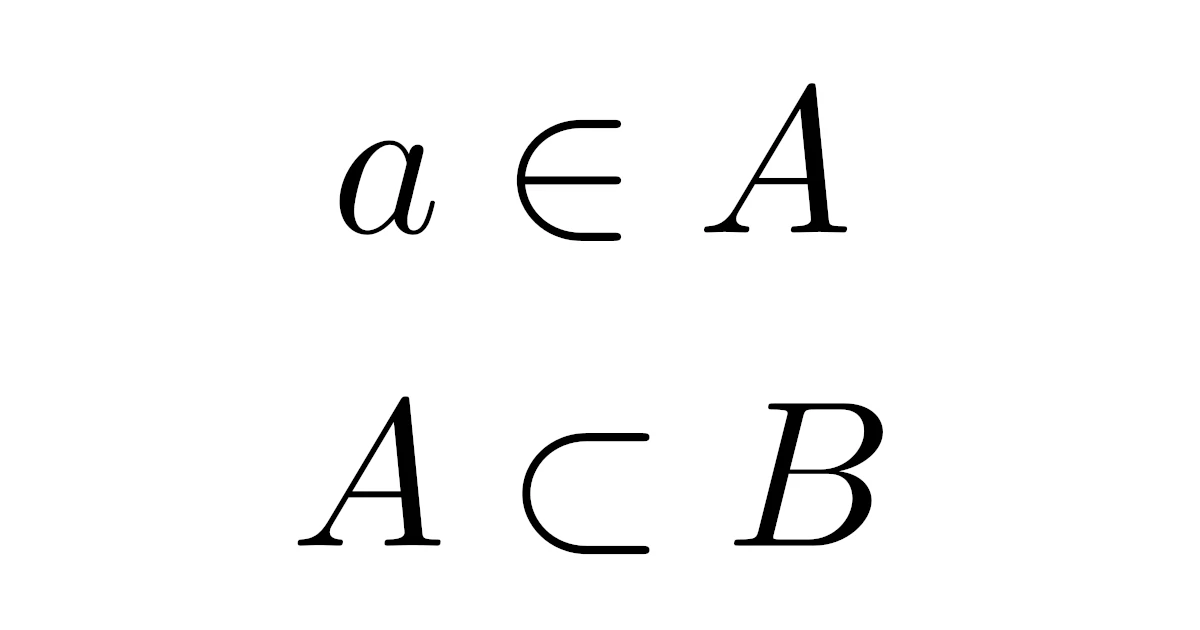
コメント