前回の記事では2つの条件$p$, $q$の関係について,必要条件と十分条件を具体例から説明しました.
なんらかの条件を考えるとき,条件を集合を用いて書き表すことで論理関係が理解しやすくなることがあります.
この記事では
- 真理集合
- 「命題の真偽」と「集合の包含」の関係
を順に説明します.
「論理と集合」の一連の記事
真理集合
整数$x$に関して,「$x$は$4$の倍数である」という条件$p$を考えましょう.
この条件$p$を満たす整数$x$の集合を$P$とすると,
ですね.このことについて,以下のように用語を定義します.
集合$U$に属する要素についての条件$p$を考える.このとき,条件$p$をみたす$U$の要素$x$全部の集合を条件$p$の真理集合という.
具体的に上の例では
- $U$は整数全部の集合
- 条件$p$は$U$の要素に関する条件
- 集合$P$は条件$p$の真理集合
ということになりますね.
「命題の真偽」と「集合の包含」の関係
いま定義した真理集合を用いて,$p\Rightarrow q$の形の命題の真偽を考えてみましょう.
定理
真理集合と命題には次の関係があります.
[命題と集合の関係] 集合$U$における条件$p$, $q$に対して,$p$, $q$の真理集合をそれぞれ$P$, $Q$とする.このとき,次は同値である.
- $p\Rightarrow q$は真である
- $P\subset Q$である
整数$x$に関する条件$p$, $q$を
- $p$:$x$は$4$の倍数である
- $q$:$x$は偶数である
とします.このとき,条件$p$の真理集合を$P$,条件$q$の真理集合を$Q$とすると,
ですから$P\subset Q$が成り立っていますね.
また,命題$p\Rightarrow q$は真ですから確かに定理の通りですね.
考え方
集合$U$における条件$p$, $q$の真理集合$P$, $Q$が
- $P\subset Q$となっているとき
- $P\subset Q$となっていないとき
の2パターンに分けて考えましょう.ポイントは$U$の要素$x$について,
- 条件$p$を満たすことと$P$に属することは同値
- 条件$q$を満たすことと$Q$に属することは同値
という点です.
パターン1
$P\subset Q$のとき,下図のようになりますね.
$P\subset Q$より$Q$に属する$x$は条件$p$をみたす$x$は必ず条件$q$をみたすことになり,これは$p\Rightarrow q$が真であるということに他なりませんね.
上に挙げた
- $p$:$x$は$4$の倍数である
- $q$:$x$は偶数である
はまさにこの状態ですね.
パターン2
$P\subset Q$でないとき,下図のいずれかになりますね.
いずれの場合も条件$p$をみたすが$q$を満たさない$x$が存在することになり,これは$p\Rightarrow q$が偽であるということに他なりませんね.
条件$p$をみたしているのに条件$q$をみたしていない場合が1つでもあれば,$p\Rightarrow q$は偽というのでした.
以上の2つのパターンから,定理が成り立つことが分かりますね.
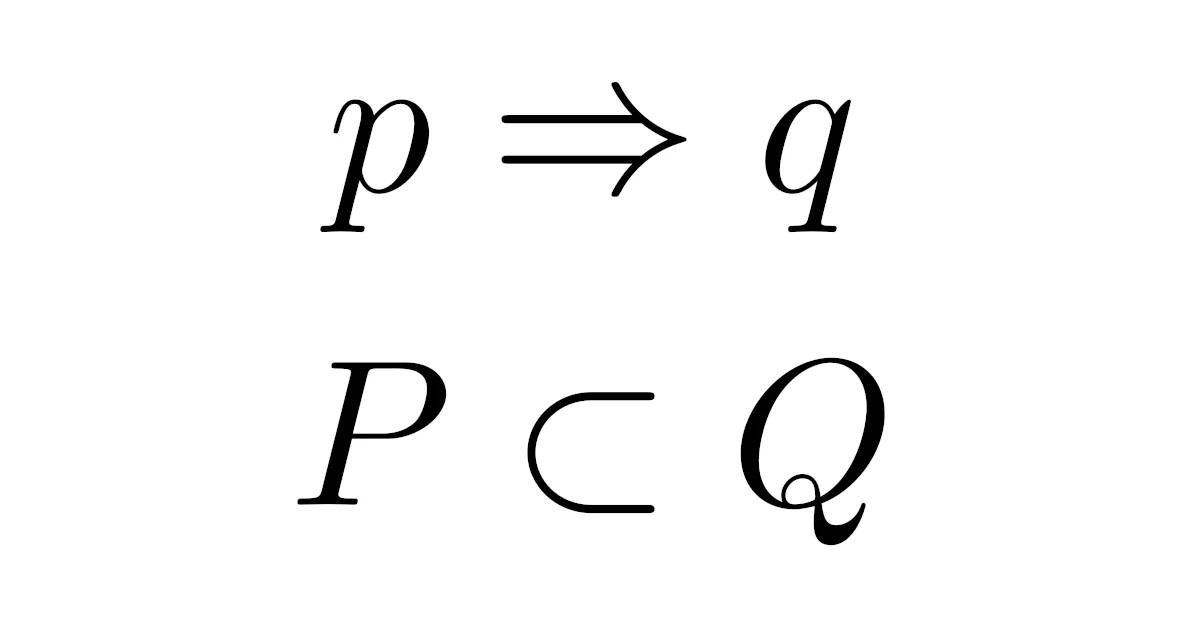
コメント