2つの集合$A$, $B$に対して,
- $A$にも$B$にも属する要素全部の集合を共通部分$A\cap B$
- $A$と$B$の少なくとも一方に属する要素全部の集合を和集合$A\cup B$
と言います.また,$A\subset U$のとき,$A$に属さない$U$の要素全部の集合を$A$の補集合と言い,$\overline{A}$と表します.
それでは和集合の補集合$\overline{A\cup B}$と,共通集合の補集合$\overline{A\cup B}$とはどのようになるでしょうか?
実は
が成り立ち,これらの等式が成り立つことをド・モルガンの法則と言います.
この記事では,
- 重要な集合(空集合,和集合,共通部分,補集合)
- ベン図
- ド・モルガンの法則
を順に説明します.
「論理と集合」の一連の記事
重要な集合
まずは
- 空集合
- 和集合
- 共通部分
- 補集合
を説明します.
空集合
ここで,重要な集合である空集合を説明しておきます.
要素を1つももたない集合を空集合といい$\emptyset$と表す.
空集合$\emptyset$を無理矢理書くなら$\{\quad\}$ということですね.
また,空集合$\emptyset$は任意の集合の部分集合であるということに注意しましょう.つまり,どんな集合$A$に対しても$\emptyset\subset A$が成り立ちます.
和集合と共通部分
2つの集合から,以下のように新しい集合を定義します.
集合$A$, $B$を集合とする.
- 「$A$, $B$の少なくとも一方に属する要素全部の集合」を$A$と$B$の和集合といい$A\cup B$と表す.
- 「$A$, $B$の両方に属する要素全部の集合」を$A$と$B$の共通部分といい$A\cap B$と表す.
和集合$A\cup B$と$A\cap B$はそれぞれ
- $A\cup B=\{x|x\in A$または$x\in B\}$
- $A\cup B=\{x|x\in A$かつ$x\in B\}$
とも表せますね.
日常での「または」は「どちらか一方」という意味で用いることが多いですが,数学での「または」は「少なくとも一方」の意味で用いることに注意してください.
そのため,数学の「または」は両方満たしていてもOKです.
次のそれぞれの集合$A$, $B$に対して,和集合$A\cup B$と共通部分$A\cap B$を求めよ.
- $A=\{1,2,3,4,5\}$, $B=\{2,4,6\}$
- $A=\{2n|n=1,2,3\}$, $B=\{2n-1|n=1,2,3\}$
(1) $A=\{1,2,3,4,5\}$, $B=\{2,4,6\}$に対して,$A\cup B=\{1,2,3,4,5,6\}$である.
また,$A\cap B=\{2,4\}$である.
(2) $A=\{2,4,6\}$, $B=\{1,3,5\}$だから,$A\cup B=\{1,2,3,4,5,6\}$である.
また,$A\cap B=\emptyset$である.
(1)のように和集合$A\cup B$において,$A$にも$B$にも属している元は1つにまとめて表します.
補集合
最後に,補集合について説明します.
集合$U$と$U$の部分集合$A$を考える.$A$に属さない$U$の要素全部の集合を$U$における$A$の補集合といい$\overline{A}$と表す.また,このときの$U$を全体集合という.
すなわち,$U$における$A$の補集合は
となりますね.
補集合を考える上でで大切なことは「どの集合の中での補集合なのか」ということです.これは常に意識しておきましょう.
集合$A=\{1,3,5\}$に対して,次のそれぞれの集合$U$における補集合$\overline{A}$を求めよ.
- $U=\{0,1,2,3,4,5\}$
- $U=\{1,3,5,7\}$
(1) $U=\{0,1,2,3,4,5\}$での$A$の補集合は$\overline{A}=\{0,2,4\}$である.
(2) $U=\{1,3,5,7,9\}$での$A$の補集合は$\overline{A}=\{7\}$である.
ベン図
数のように閉じた曲線で集合を模した図をベン図といいます.べン図は集合を視覚的に表す際によく用いられます.
全体集合$U$と集合$A$, $B$に対して
- 共通部分$A\cap B$
- 和集合$A\cup B$
- $A$の補集合$\overline{A}$
は下図のようになりますね.
ド・モルガンの法則
和集合の補集合,共通部分の補集合に対して,次のド・モルガンの法則が成り立ちます.
[ド・モルガンの法則] 全体集合が同じ集合$A$, $B$に対し,次の等式が成り立つ.
- $\overline{A\cap B}=\overline{A}\cup\overline{B}$
- $\overline{A\cup B}=\overline{A}\cap\overline{B}$
それぞれ
- 共通部分の補集合は,補集合の和集合
- 和集合の補集合は,補集合の共通部分
ということができますね.
形式的には$\overline{\cap}=\cup$, $\overline{\cup}=\cap$ということですね.
以下,全体集合を$U$とし,ド・モルガンの法則が成り立つことをベン図から考えてみましょう.
$\overline{A\cap B}=\overline{A}\cup\overline{B}$の考え方
$\overline{A}$と$\overline{B}$をそれぞれベン図で表せば,下図のようになりますね.
よって,これらの和集合$\overline{A}\cup \overline{B}$は下図のようになります.
これは$A\cap B$の補集合$\overline{A\cap B}$なので,
が成り立つことが分かりますね.
$\overline{A\cup B}=\overline{A}\cap\overline{B}$の考え方
同様の考え方により,$\overline{A\cup B}=\overline{A}\cap\overline{B}$が成り立つことも分かります.
$\overline{A}$と$\overline{B}$をそれぞれベン図で表せば,
なので,この共通部分$\overline{A}\cap \overline{B}$は下図のようになりますね.
これは$A\cup B$の補集合$\overline{A\cup B}$なので,
が成り立つことが分かりました.
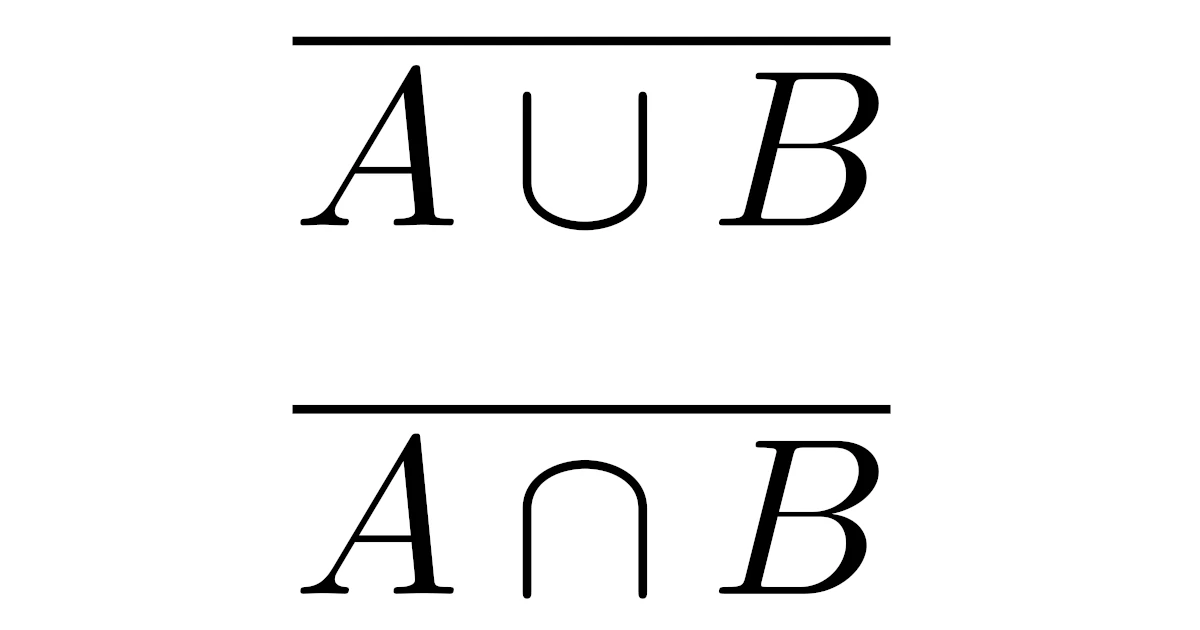
コメント