数学において(数学でなくとも)仮定・結論を意識することはとても大切です.
さて,数学では「$p$ならば$q$である」という形の主張がよく登場します.
この記事では,論理の基本として
- 命題と条件
- 必要条件と十分条件
を順に説明します.
「論理と集合」の一連の記事
命題と条件
まずは条件と命題を説明します.
命題
例えば,
- $2$は偶数である
- $5$は$4$で割り切れる
と言っている人がいたとしましょう.
これらの主張のうち,(1)は正しいものの,(2)は誤りですね.
これについて,次のように命題というものを定義しましょう.
正しいか否かが明確に決まる主張を命題という.また,命題が正しいとき命題は真であるといい,命題が正しくないとき命題は偽であるという.
命題でないものとしては,
- 彼女は頭が良い
- 彼は背が高い
などは,正しいか否かが明確には決まりませんから命題ではありません.
しかし,これらを
- 彼女の直近の試験の成績は学年1位である
- 彼の身長は180cm以上である
という主張に変えれば,正しいか正しくないかが明確に決まるのでこれらは命題です.
また,上の例について
- 「$2$は偶数である」は真
- 「$5$は$4$で割り切れる」は偽
というわけですね.
条件
数学では「$p$ならば$q$である」という形の命題がよく登場します.例えば,
- 整数$x$に対して,$x$が$4$の倍数ならば,$x$は偶数である
- 三角形$\mrm{X}$に対して,$\mrm{X}$が二等辺三角形ならば,$\mrm{X}$は正三角形である
などですね.なお,(1)は真ですが,(2)は偽ですね.
命題「$p$ならば$q$である」が真と言えるのは「$p$となるとき必ず$q$となるとき」であり,$p$が成り立っているのに$q$が成り立っていない場合が1つでもあれば「$p$ならば$q$である」は偽です.
さて,この命題「$p$ならば$q$である」において$p$や$q$のことを条件といいます.
対象$x$を含んだ文や式を$x$の条件という.
例えば,上の例(1)では
- $x$は$4$の倍数
- $x$は偶数
は整数$x$の条件で,また上の例(2)では
- $\mrm{X}$は二等辺三角形
- $\mrm{X}$は正三角形
は三角形$\mrm{X}$の条件です.
必要条件と十分条件
「$p$ならば,$q$である」型の命題については必要条件と十分条件という概念が重要です.
条件$p$, $q$に対して,命題「$p$ならば$q$である」を$p\Rightarrow q$と表す.命題$p\Rightarrow q$が真であるとき,
- $p$は$q$の十分条件である
- $q$は$p$の必要条件である
という.また,命題$p\Rightarrow q$と命題$q\Rightarrow p$がともに真であるとき,$p$は$q$の必要十分条件である,または$p$と$q$は同値であるという.
この定義から
- $p$は$q$の十分条件である
- $q$は$p$の必要条件である
は全く同じ意味であり,
- $p$は$q$の必要条件である
- $q$は$p$の十分条件である
全く同じ意味であることに注意してください.
$p$が$q$の必要条件・十分条件であるかを調べるときのポイントは,
- $p\Rightarrow q$の真偽($p$が成り立つとき,必ず$q$が成り立つか?)
- $q\Rightarrow p$の真偽($q$が成り立つとき,必ず$p$が成り立つか?)
を考えるということです.
いくつか具体的に考えてみましょう.
具体例1
次の条件$p$, $q$はそれぞれ他方の必要条件か,十分条件か.
- $p$;A君はX高校の生徒である
- $q$:A君は高校生である
$p$が$q$の十分条件($q$が$p$の必要条件)であるかどうかは,命題$p\Rightarrow q$の真偽を考えればよいですね.
また,$q$が$p$の必要条件($p$が$q$の十分条件)であるかどうかは,命題$q\Rightarrow p$の真偽を考えればよいですね.
(1)$p\Rightarrow q$の真偽:A君はX高校の生徒(条件$p$)であるとき,必ずA君は高校生(条件$q$)でしょうか?
X高校に生徒として通っているということは,必ず高校生ということになりますね.
つまり,命題「$p\Rightarrow q$」は真ですから,$p$は$q$の十分条件($q$は$p$の必要条件)ですね.
(2)$q\Rightarrow p$の真偽:A君は高校生(条件$q$)とするとき,必ずA君はX高校の生徒(条件$p$)でしょうか?
たとえば,A君はY高校の生徒かもしれませんし,Z高校の生徒かもしれませんから,必ずしもA君がX高校の生徒であるとは言えません.
つまり,命題「$q\Rightarrow p$」は偽ですから,$p$は$q$の必要条件ではない($q$は$p$の十分条件ではない)ですね.
(1), (2)より$p$は$q$の十分条件だが必要条件でない($q$は$p$の必要条件だが十分条件でない)と分かりました.
具体例2
次の条件$p$, $q$はそれぞれ他方の必要条件か,十分条件か.
- $p$:$x$は偶数である
- $q$:$x$は4の倍数である
(1)$p\Rightarrow q$の真偽:$x$は偶数(条件$p$)とするとき,必ず$x$は$4$の倍数(条件$q$)でしょうか?
たとえば,$x=6$は$p$をみたしますが,$q$は満たしていません.
つまり,命題「$p\Rightarrow q$」は偽ですから,$p$は$q$の十分条件ではない($q$は$p$の必要条件ではない)ですね.
(2)$q\Rightarrow p$の真偽:$x$は$4$の倍数(条件$q$)とするとき,必ず$x$は偶数(条件$p$)でしょうか?
$x$が4の倍数であるとき,$x$は整数$m$によって$x=4m$と表せますね.このとき,$x=2\times2m$であり,$2m$は整数ですから$x$は偶数ですね.
つまり,命題「$q\Rightarrow p$」は真ですから,$p$は$q$の必要条件($q$は$p$の十分条件)ですね.
(1), (2)より$p$は$q$の必要条件だが十分条件でない($q$は$p$の十分条件だが必要条件でない)と分かりました.
具体例3
次の条件$p$, $q$はそれぞれ他方の必要条件か,十分条件か.
- $p$:$x$は$6$の倍数である
- $q$:$x$は$2$の倍数かつ$3$の倍数である
(1)$p\Rightarrow q$の真偽:$x$は$6$の倍数(条件$p$)とするとき,必ず$x$は$2$の倍数かつ$3$の倍数である(条件$q$)でしょうか?
$x$が$6$の倍数であるとき,$x$は整数$m$によって$x=6m$と表せますね.このとき,
であり,$2m$と$3m$はともに整数ですから$x$は$3$の倍数かつ$2$の倍数ですね.
つまり,命題「$p\Rightarrow q$」は真ですから,$p$は$q$の十分条件($q$は$p$の必要条件)ですね.
(2)$q\Rightarrow p$の真偽:$x$は$2$の倍数かつ$3$の倍数である(条件$q$)とするとき,必ず$x$は$6$の倍数(条件$p$)でしょうか?
$x$が$2$の倍数であるとき,$x$は整数$m$によって$x=2m$と表せます.さらに,$x=2m$が$3$の倍数であれば,$m$が$3$の倍数でなければなりませんから,$m$は整数$n$によって$m=3n$と表せます.
よって,$x=6n$となり$x$は$6$の倍数です.
つまり,命題「$q\Rightarrow p$」は真ですから,$p$は$q$の必要条件($q$は$p$の十分条件)ですね.
(1), (2)より$p$は$q$の必要十分条件($q$は$p$の必要十分条件)と分かりました.
以上のように,
- 真の場合は証明
- 偽の場合は反例
を考えればよいというわけですね.
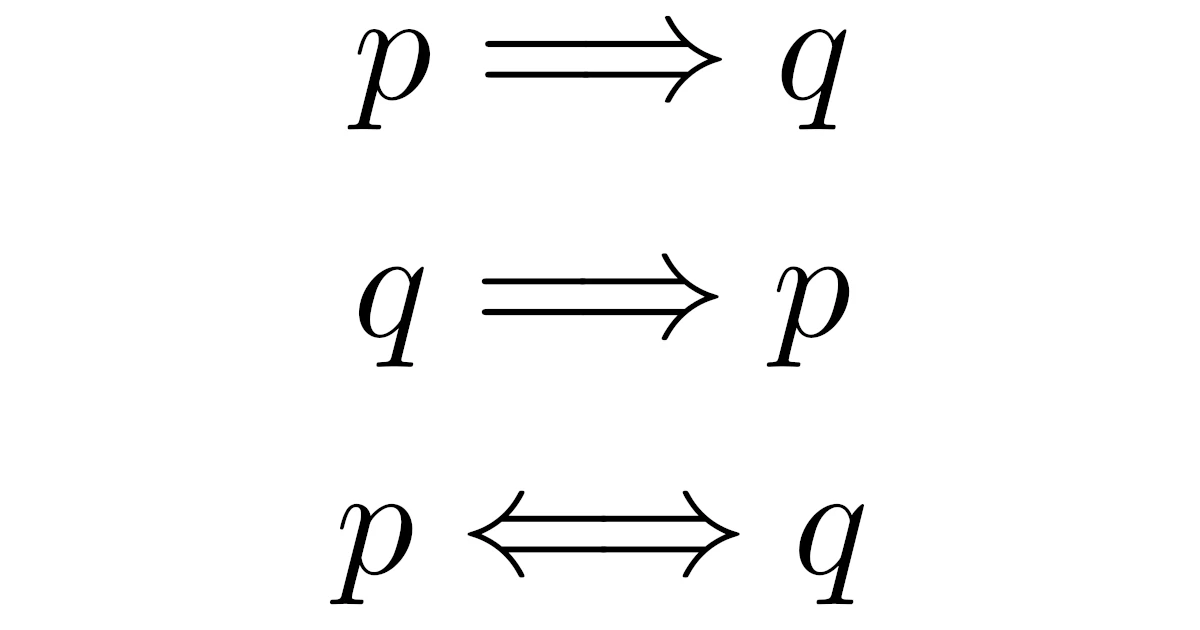
コメント