例えば,不定積分
は部分積分を用いて計算するのが常套手段で,教科書にも載っている基本問題ですね.
しかし,これらの問題は部分積分を何回も使う必要があり,計算量が多くなり計算ミスをしがちな問題でもあります.とくにプラスマイナスの符号ミスがよくみられます.
そこで,この記事では部分積分を使わず計算量を減らすことができる計算方法を紹介します.
部分積分の公式と積の微分公式
まずは部分積分の公式を思い出しておきましょう.
[部分積分] 微分可能な関数$f(x)$, $g(x)$に対して,
が成り立つ.ただし,$’$は微分を表す.
この部分積分の公式は次のように導出されます.
積の微分公式より
である.導関数を積分すると元に戻ることに注意すると,両辺$x$に関して積分して
が成り立つ.
さて,この導出で大切なことは積の微分公式から部分積分の公式が導出できるということです.
したがって,部分積分の公式を用いて計算できる積分は,積の微分公式を使っても計算できるはずですね.
ポイントは積の微分公式$(f(x)g(x))’=f'(x)g(x)+f(x)g'(x)$の$f'(x)g(x)$の部分が,計算したい積分$\dint f'(x)g(x)\,dx$に対応しているところです.
これがどうポイントなのかは,この後の具体例で説明していきます.
積の微分公式による積分の具体例
それでは具体的に部分積分の公式を使わずに,積の微分公式から積分を計算してみましょう.
例1
不定積分$\dint xe^x\,dx$を求めよ.
積の微分公式で$(f(x)g(x))’=f'(x)g(x)+f(x)g'(x)$の$f'(x)g(x)$の部分が,計算したい積分$\dint f'(x)g(x)\,dx$になるので,$f'(x)g(x)=xe^x$となるように$f(x)$と$g(x)$を考えるわけです.
つまり,「何を微分すれば$xe^x$が出てくるのか」と考えるわけですね.
そう考えると$f(x)=e^{x}$, $g(x)=x$とすれば,$f'(x)=e^x$なので$f'(x)g(x)=xe^{x}$となって良さそうな気がしますね.
$xe^{x}$を$x$で微分すると
なので,この両辺を$x$で積分して
を得る.ただし,$C$は積分定数である.
なお,部分積分の公式を使って積分するなら
となります.この2つ目の等号が上で積の微分公式を用いた解答の$xe^{x}=(xe^{x})’-e^{x}$と対応していることが見てとれますね?
例2
上の例1くらいなら普通の部分積分の公式でも間違えなさそうですが,何回も部分積分をするような問題ほどこの考え方の良さが分かります.
例えば,次の問題は2回部分積分することで求まる不定積分として教科書に載っていますね.
不定積分$\dint e^x\sin{x}\,dx$を求めよ.
先ほどの問題と同様に,この問題では「何を微分すれば$e^x\sin{x}$が出てくるのか」を考えましょう.
今回の積分でも$e^x$が微分しても変化しないことに注目して,
となりますね.
しかし,少し困りました.この両辺を$x$で積分すると$\dint e^{x}\cos{x}\,dx$という今は出てきて欲しくないものが出てきそうです.
そこで,加えて「何を微分すれば微分して$e^{x}\cos{x}$が出てくるのか」を考えて,
を準備します.
こうすると,$e^x\cos{x}$が出てきますから,$(1)$と$(2)$の辺々を引けば$e^x\cos{x}$が消えてうまく$\int e^x\sin{x}\,dx$がもとまりそうですね.
$e^{x}\sin{x}$と$e^{x}\cos{x}$を$x$で微分すると,
なので,辺々引いて
となる.よって,この両辺を$x$で積分して
を得る.ただし,$C$は積分定数である.
例2の問題の前にも書きましたが,$\dint e^{x}\sin{x}\,dx$は部分積分を2回使うことで計算できるのでした.
そう考えると,(1)と(2)で積の微分公式を2回使うことにも納得できますね.
例3
最後に3回部分積分を使うことで計算できる積分を,積の微分公式で計算しましょう.
不定積分$\dint e^x\sin{x}\cos{x}\,dx$を求めよ.
この問題では,「何を微分すれば$e^x\sin{x}\cos{x}$が出てくるのか」と考えれば良いですね.
$e^{x}\sin{x}\cos{x}$, $e^{x}\cos^{2}{x}$, $e^{x}\sin^{2}{x}$を$x$で微分すると
だから,$(1)-(2)+(3)$より
となる.この両辺を$x$で積分して
を得る.
最初に考える(1)では$x$で積分すると$\dint e^{x}\cos^{2}{x}\,dx$と$\dint e^{x}\sin^{2}{x}\,dx$が出てきます.
これを消すために(2)と(3)を考えているわけですね.
やはり部分積分を3回使う問題は,対応する積の微分公式を3回使うことで求められていますね.
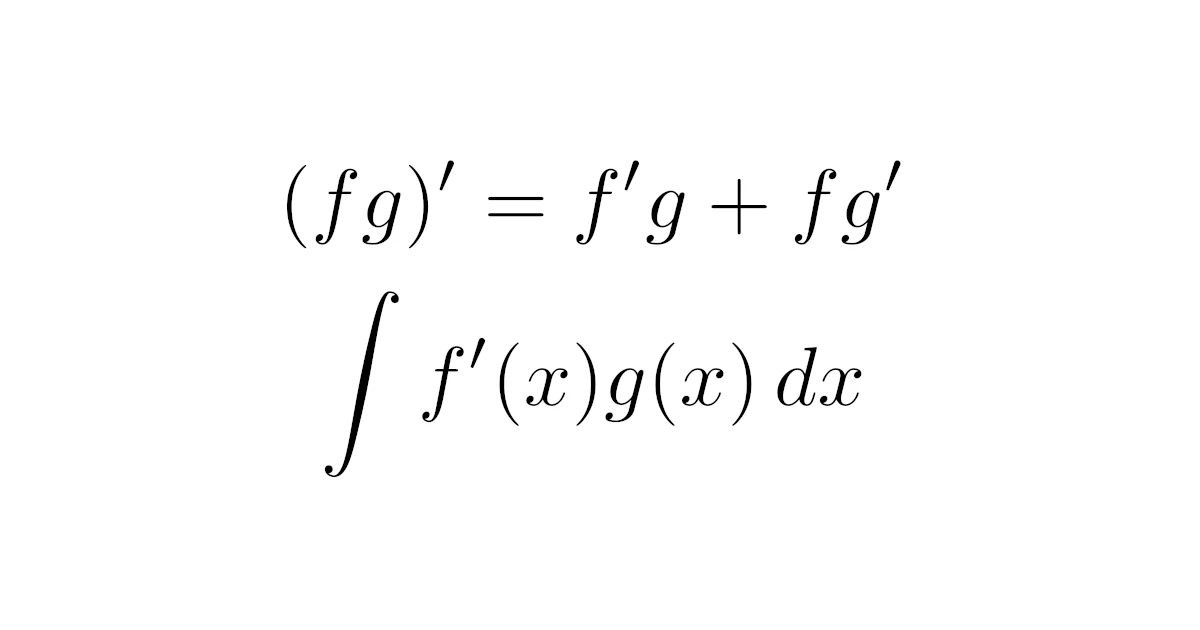
コメント