バネは縮められると伸びようとし,伸ばされると縮もうとします.
この変形させられると元の形に戻ろうとするバネの力を弾性力といいます.
また,バネを押し縮めれば押し縮めるほど押し返す力が強くなり,一方でバネを引き伸ばせば引き伸ばすほど縮もうとする力が強くなります.
このように,変形させればさせるほど力強く元に戻ろうとする法則はフックの法則と呼ばれ,フックの法則から弾性力の大きさを計算することができます.
この記事では
- 弾性力の基本
- フックの法則
- 弾性力の具体例
を順に説明します.
「力学の基本」の一連の記事
弾性力
日常的にもよく見かけるバネは弾性力をもつものの代表ですね.
弾性力の向き
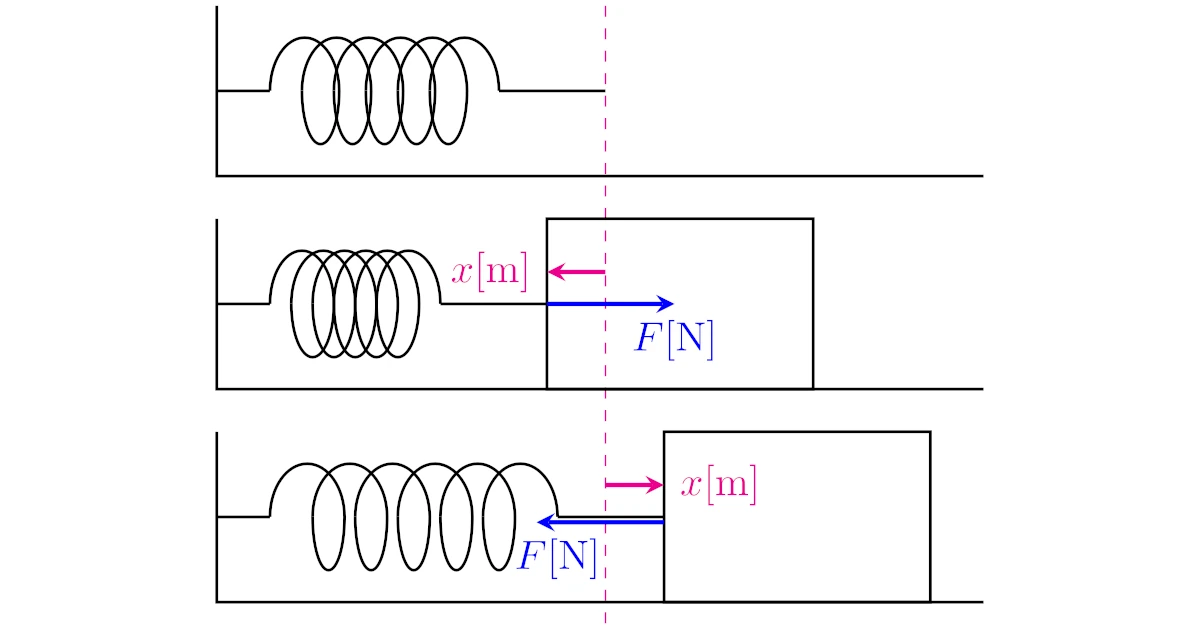
バネの弾性力を考える際には,伸びも縮みもしていない長さが基準となります.
力が加わっていないバネはある長さの状態で静止する.このバネの長さのことを自然長や自然の長さなどという.
自然長はバネによって異なります.
「自然長」という言葉を用いると
- バネが縮んでいる$\iff$バネが自然長より短い
- バネが伸びている$\iff$バネが自然長より長い
と言い換えることができますね.
変形させられたバネが自然長に戻ろうとしてはたらく力を弾性力という.すなわち,
- バネが自然長より短いときはバネが伸びる向き
- バネが自然長より長いときはバネが縮む向き
に弾性力がはたらく.
他にゴムひもは伸ばされたときのみ弾性力がはたらくものですね.
弾性力の大きさ
弾性力の大きさを求めることができる法則としてフック(Hooke)の法則があります.
[フックの法則]バネの弾性力の大きさ$F[\mrm{N}]$は,バネの自然長からの長さの変化$x[\mrm{m}]$に比例する.すなわち,$F=kx$が成り立つ.
このときの比例定数$k[\mrm{N/m}]$をバネ定数という.
バネ定数$k$はバネによって決まっており,バネ定数$k$が大きいほど小さい$x$で大きな弾性力$F$が得られます.
つまり,硬いバネほどバネ定数が大きいということができますね.
フックの法則のロバート・フック氏はアイザック・ニュートン氏の少し先輩にあたる時代の物理学者です.
弾性力の例題
いくつか具体例を考えましょう.
例1(天井から物体をバネで吊した場合)
質量$m[\mrm{kg}]$の物体を天井から軽いバネで吊るすと,バネが自然長から$\ell[\mrm{m}]$伸びて物体は静止した.このときのバネ定数$k[\mrm{N/m}]$を求めよ.
ただし,重力加速度の大きさを$g[\mrm{m/s^{2}}]$とし,バネ自身の重さは無視できるとする.
物体が静止することから,物体にはたらく力がつり合っていることが分かります.
物体にはたらく力は重力と弾性力なので,これらの力のつりあいを考えればよいですね.
物体の質量が$m[\mrm{kg}]$,重力加速度が$g[\mrm{m/s^2}]$なので,物体にはたらく重力の大きさは$mg[\mrm{N}]$である(鉛直下向き).
一方,バネ定数が$k[\mrm{N/m}]$,バネが自然長から$\ell[\mrm{m}]$伸びていることから,フックの法則より弾性力の大きさは$k\ell[\mrm{N}]$である(鉛直下向き).
他に物体に力ははたらいておらず,静止していることから物体にはたらく力はつり合っているので,
とバネ定数$\dfrac{mg}{\ell}$を得る.
例2(天井から物体を2本のバネで吊した場合)
質量$m[\mrm{kg}]$の物体を天井から軽い2本の同じバネで吊るすと,両方のバネが自然長から$\ell[\mrm{m}]$伸びて物体は静止した.このときのバネ定数を求めよ.
ただし,重力加速度の大きさを$g[\mrm{m/s^{2}}]$とし,バネ自身の重さは無視できるとする.
この例でも物体が静止することから,物体にはたらく重力と2つの弾性力の力のつりあいを考えればよいですね.
物体の質量が$m[\mrm{kg}]$,重力加速度が$g[\mrm{m/s^2}]$なので,物体にはたらく重力の大きさは$mg[\mrm{N}]$である(鉛直下向き).
一方,バネ定数が$k[\mrm{N/m}]$,バネが自然長から$\ell[\mrm{m}]$伸びていることから,フックの法則より2つの弾性力の大きさはともに$k\ell[\mrm{N}]$である(鉛直下向き).
他に物体に力ははたらいておらず,静止していることから物体にはたらく力はつり合っているので,
とバネ定数$\dfrac{mg}{2\ell}$を得る.
コメント