水平な地面にボールを転がすと,ボールの動きはだんだん緩やかになり,やがては止まります.
これはボールの動きを妨げる向きに地面から摩擦力を受けていることが原因です.
摩擦力は物体と物体が触れていればはたらく可能性があり,物体が触れている場合にはいつでも摩擦力がはたらくかどうかは気にしたいところです.
また,摩擦力の大きさは
- 物体が静止しているとき
- 物体が動いているとき
- 物体がギリギリ動かないとき
のどの場合かによって考え方が変わるところが少し難しいところです.
この記事では
- 摩擦力とは何か?
- 摩擦力の3パターンの力の大きさ
を順に説明します.
「力学の基本」の一連の記事
摩擦力
以下では,下図のように「床に置いた物体に糸をつけて,大きさ$F[\mrm{N}]$の水平方向に引っ張る」という状況を考えます.
このとき,床と物体の間には「運動を止めようとする向き」に力がはたらきます.この力を摩擦力といいます.
冒頭でも説明したように摩擦力の大きさは3パターンで考え方が変わります.
以下では,3パターンに分けて摩擦力の大きさを説明します.
摩擦力の大きさ
摩擦力の大きさを
- 物体が静止しているとき
- 物体が動いているとき
- 物体がギリギリ動かないとき
の3パターンに分けて説明します.
パターン1:物体が静止しているとき
物体に繋げた糸を少し引っ張っただけでは物体は動きません.
一般に静止している物体にはたらく力はつりあっているのでした.
物体にはたらく力がつりあっているというは,物体にはたらく力の合力の大きさが$0$と言うことですから,
- 糸を引っ張る力
- 摩擦力
の大きさは等しいということになります.そのため,摩擦力は大きさは加えた力と同じで$F[\mrm{N}]$と分かりますね.
物体に水平方向の大きさ$F[\mrm{N}]$の力を加える.
このとき,物体が静止していれば,加えた力と逆向きに大きさ$F[\mrm{N}]$の摩擦力が地面と物体の間にはたらく.
よって,糸を引く力の大きさ$F[\mrm{N}]$を少しずつ大きくしていくと,それに伴って摩擦力も大きくなっていきます.
物体が静止している以上,必ず力はつりあっているので摩擦力は常に引く力と同じ大きさとなります.
このように,物体が動いていない限り糸を引く力の方が大きかったり,摩擦力の方が大きかったりといったことがあり得ないことは当たり前にしておきましょう.
パターン2:物体が動くとき
物体に繋げた糸をある程度強く引っ張ると物体が動き始めますが,少し抵抗も感じますね.
このように,物体が動いているときにも摩擦力ははたらきます.
さて,日常の経験から床の上で机などの物体を押すとき,速く押してもゆっくり押しても摩擦力は変わらない気がしませんか?実は一般に次が成り立ちます.
移動している物体にはたらく摩擦力は,その速さによらず大きさは一定である.
また,日常の経験から物体の質量(厳密には地面からの垂直抗力)が大きいほど,このときの摩擦力の大きさも大きいことも明らかでしょう.
実際,動いている時の物体と地面の間にはたらく摩擦力の大きさは,物体と地面の間にはたらく垂直抗力の大きさに比例します.
このときの比例係数$\mu’$を動摩擦係数といいます.
つまり,次が成り立ちます.
物体と地面の間に$N[\mrm{N}]$の垂直抗力がはたらいている物体に,水平方向の大きさ$F[\mrm{N}]$の力を加える.
このとき,物体が動くならば,加えた力と逆向きに大きさ$\mu’N[\mrm{N}]$の摩擦力がはたらく.ただし,$\mu’$は動摩擦係数である.
なお,動摩擦係数は床と物体の相性によって決まります.例えば,ゴムとゴムの間の動摩擦係数は大きいですし,氷とガラスの間の動摩擦係数はとても小さいです.
実際の問題では動摩擦係数は与えられていることがほとんどです.
パターン3:物体がギリギリ動かないとき
物体に繋げた糸を引く力を徐々に強くしていくと物体が動き始める瞬間がありますが,このギリギリの場合の摩擦力を考えましょう.
これは動き出す直前の静止摩擦力ということもできますね.
動き出すために必要な力の大きさは物体と床の「相性」のみによって決まり,この「動き出すギリギリの摩擦力の大きさ」を最大静止摩擦力といい,この大きさを$\mu N[\mrm{N}]$と表します.
ここで,$N[\mrm{N}]$は地面と物体の間にはたらく垂直抗力で,$\mu$を静止摩擦係数といいます.
一方,動き出す直前ということは物体はまだ静止している状態なので,加えた力と摩擦力の大きさはつりあっており,摩擦力の大きさは$F[\mrm{N}]$でもあります.
物体と地面の間に$N[\mrm{N}]$の垂直抗力がはたらいている物体に,水平方向の大きさ$F[\mrm{N}]$の力を加える.
このとき,物体が動く直前の状態ならば,加えた力と逆向きに大きさ$\mu N[\mrm{N}]=F[\mrm{N}]$の摩擦力がはたらく.ただし,$\mu$は静止摩擦係数である.
静止摩擦係数$\mu$が登場するのはこのギリギリの場合だけで,ギリギリでない場合の静止摩擦力では用いられないことに注意してください.
力と摩擦力のグラフ
物をぐーっと押していき一旦スッと動き出すと,動かし始めるときほど力を入れなくても動き続けることを,日常的に感じたことはあるのではないでしょうか?
実はその実感は正しく,動き始めてからの方が動かし始める瞬間より摩擦力は小さくなります.
このことは,以下のように言い換えることができます.
同じ物体間での静止摩擦係数$\mu$と動摩擦係数$\mu’$は$\mu>\mu’$をみたす.
言い換えれば,「最大静止摩擦力は動摩擦力より大きい」ということになります.
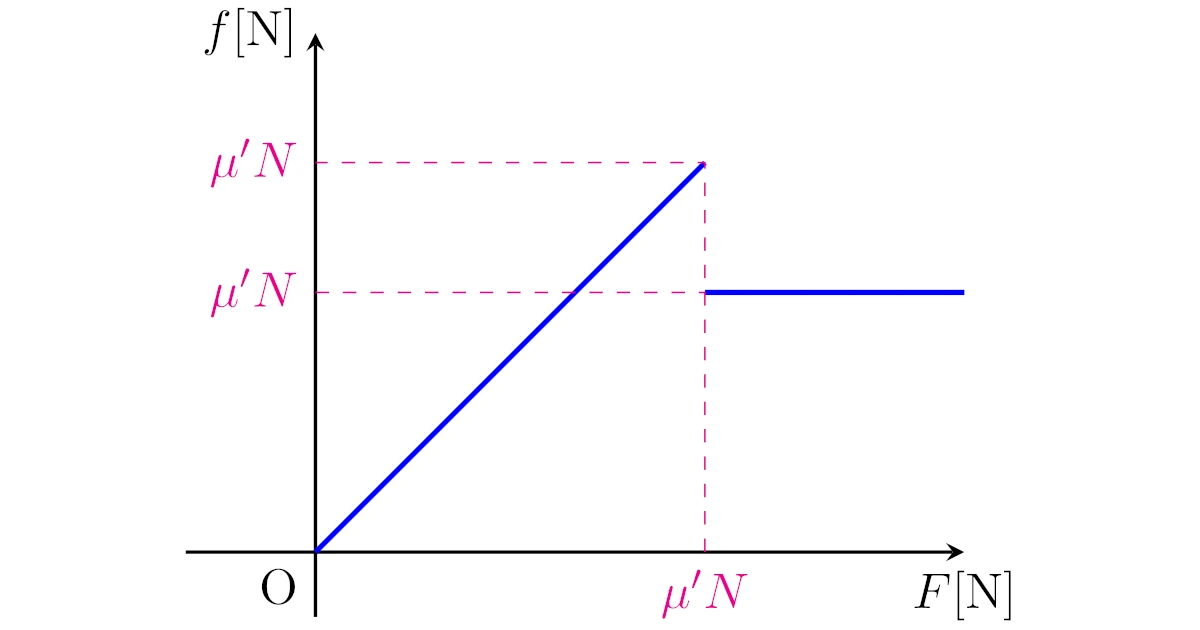
これを踏まえると,物体に加える力$F[\mrm{N}]$の大きさと摩擦力$f[\mrm{N}]$の大きさの関係は次のグラフのようになります.
コメント