運動方程式の基本｜力がつり合っていなくても成り立つ等式

物体の運動を考えるとき，どのように物体に力がはたらいているかを把握することは大切です．

とくに物体にはたらく力がつり合っていれば，静止している物体は静止し続けます．

一方，力がつり合っていなければ，静止している物体も動き始めることになりますが，このときは運動方程式によって物体の運動を考えることができます．

この記事では

を順に説明します．

「力学の基本」の一連の記事

運動方程式とは何か？

前提となる事実をひとつ確認してから運動方程式を説明します．

一定の向きに同じ大きさの力がはたらいている物体は，その力の向きに等加速度直線運動をする．

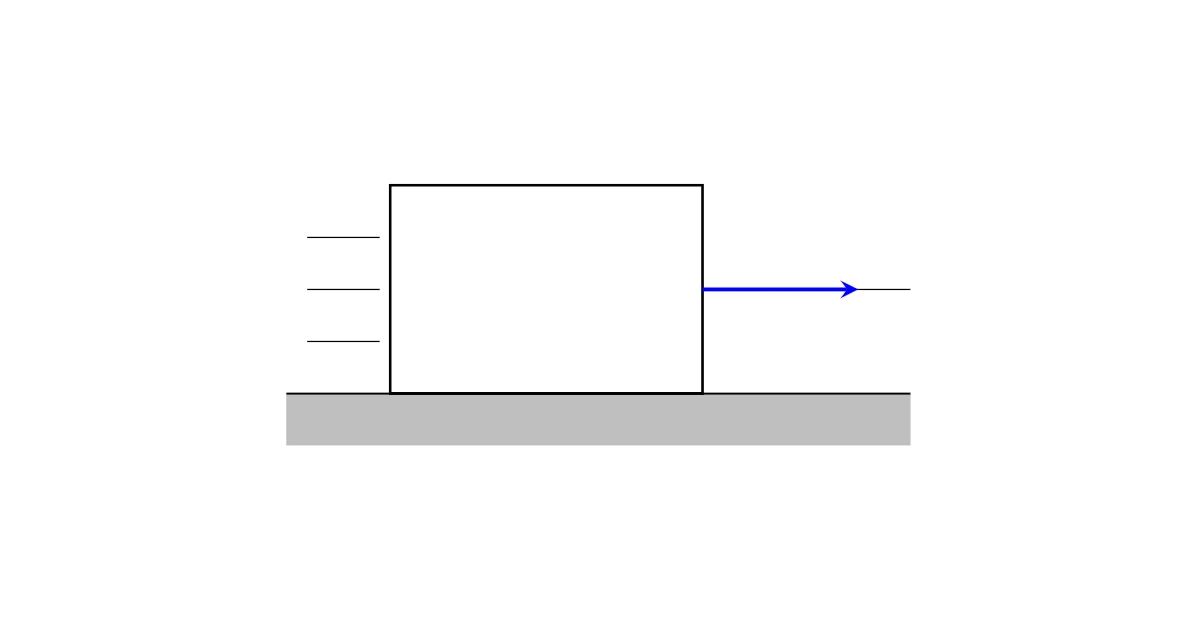
例えば，物体を同じ力で引っ張り続けると，最初は遅くても力を加えている方向に少しずつ加速していきます．

自由落下する物体には重力が常に鉛直下向きにはたらきます．

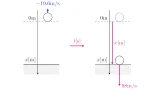
重力は一定なので，真空中を自由落下する物体は鉛直下向きに等加速度運動をします．

いまの事実に加えて，どれくらいの大きさの力を与えれば，どれくらいの大きさの加速度を得るかまで分かると，物体がどのように運動するかが分かりそうです．

この力の大きさと加速度の大きさの関係について述べたものが運動方程式で，次のようになります．

質量$m$の物体に大きさ$F$の力がはたらき，物体は大きさ$a$の加速度を得たとする．このとき，

$\begin{align*}F=ma\end{align*}$

が成り立つ．この等式を運動方程式という．

「ニュートンの運動方程式」ということもあります．

先ほどの事実は「力$F$の向きと加速度$a$の向きの関係」について述べており，この運動方程式では「力$F$の大きさと加速度$a$の大きさの関係」について述べたものになっています．

ベクトルは大きさと向きを同時に表すものなので，これら２つを併せると次のようになりますね．

［運動方程式（ベクトル）］質量$m$の物体に力$\ve{F}$がはたらき，物体は加速度$\ve{a}$を得たとする．このとき，

$\begin{align*}\ve{F}=m\ve{a}\end{align*}$

が成り立つ．

物理では力・位置・速度・加速度など，大きさと向きをもつものはベクトルで表すことがよくありますね．

物体にはたらく力がつり合っているときの物体の運動は運動方程式を用いて説明することができます．

力がつりあっているとき，運動している物体は等速直線運動をする．

逆に，等速直線運動をしているとき，物体にはたらく力はつりあっている．

この事実は運動方程式を用いても説明してみましょう．

力がつり合っているというのは，物体にはたらく合力の大きさが０ということですから，運動方程式$\ve{F}=m\ve{a}$において$\ve{F}=\ve{0}$を考えることになります．

よって，$\ve{0}=m\ve{a}$なので両辺を$m$で割って$\ve{a}=\ve{0}$となり，確かに物体は等速直線運動をすることになりますね．

逆に，物体が等速直線運動をするということは物体の加速度の大きさが０ということなので，運動方程式$\ve{F}=m\ve{a}$で$\ve{a}=\ve{0}$とすると$\ve{F}=\ve{0}$なので，確かに物体にはたらく力はつりあいますね．

運動方程式の使い方の具体例については，例えば以下の記事を参照してください．