お風呂でお湯に浸かると体が軽く感じますが,これは水に浸かることで体に浮力がはたらくことが理由です.
別の例を挙げれば,水に木片を入れると木片が水に浮くのは,水中で木片にはたらく重力よりも浮力の方が大きいことが理由です.
このように,液体が物体を浮かせる力のこと浮力と言います.
実は浮力は液体中だけではなく,気体中など(流体中)でもはたらきます.例えば,プロペラが回ってヘリコプターの機体が浮くのも実は浮力がはたらいていることが理由です.
しかし,高校物理で扱う浮力は液体が物体を浮かせる力に限ることがほとんどなので,この記事でもこの場合のみ扱います.
さて,物体にはたらく浮力は
- 物体が完全に沈んでいる場合
- 水面に浮かんでいる場合
のどちらでも,浮力の原理を理解していれば同じ考え方で浮力の大きさを求めることができます.
「力学の基本」の一連の記事
浮力
浮力の大きさを求めるためには液体の密度が重要です.
そこで,浮力を説明する前に密度について復習しておきましょう.
密度の復習
物体の単位体積あたりの質量を密度という.なお,密度はギリシャ文字の$\rho$で表すことが多い.
もし「単位体積あたり」という言葉に戸惑ってしまう人がいれば,次の具体例をイメージしてください.
体積$1[\mrm{m^3}]$の物体の質量が$M[\mrm{kg}]$のとき,密度は$M[\mrm{kg/m^3}]$である.
「密度」の定義に「単位体積」という言葉を使うのは,単位が$[\mrm{m^3}]$とは限らないからです.場合によっては$[\mrm{cm^3}]$や$[\mrm{mm^3}]$かもしれません.
密度で大切なことは物体の質量が$1[\mrm{m^3}]$だろうが,$2[\mrm{m^3}]$だろうが,$3[\mrm{m^3}]$だろうが,同じ物質なら密度は全て同じという点です.
例えば,次の問題を考えてみましょう.
次の物体の密度を大きい順に並べよ.
- 半径$1[\mrm{m}]$の鉄球
- 半径$1[\mrm{cm}]$の鉄球
- 1辺の長さが$1[\mrm{cm}]$の立方体の鉄
- 形がぐちゃぐちゃな$1[\mrm{kg}]$の鉄の塊
密度は形にも質量にも一切関係せず,素材が同じなら全て等しいので,答えは
どれも素材が鉄なので,密度は全て等しい.
となりますね.
この記事では使いませんが,ついでに(ほぼ定義の)次の公式も当たり前にしておきましょう.
質量$m[\mrm{kg}]$の物体の体積$V[\mrm{m^3}]$なら,この物体の密度は$\dfrac{m}{V}[\mrm{kg/m^3}]$である.
体積$V[\mrm{m^3}]$の物体の質量が$m[\mrm{kg}]$であったとすると,この物体の体積$1[\mrm{m^3}]$の物体の質量は$\dfrac{m}{V}[\mrm{kg}]$ですから,密度は$\dfrac{m}{V}[\mrm{kg/m^3}]$となりますね.
浮力の大きさ
結論から言えば,浮力の向きと大きさは次の通りです.
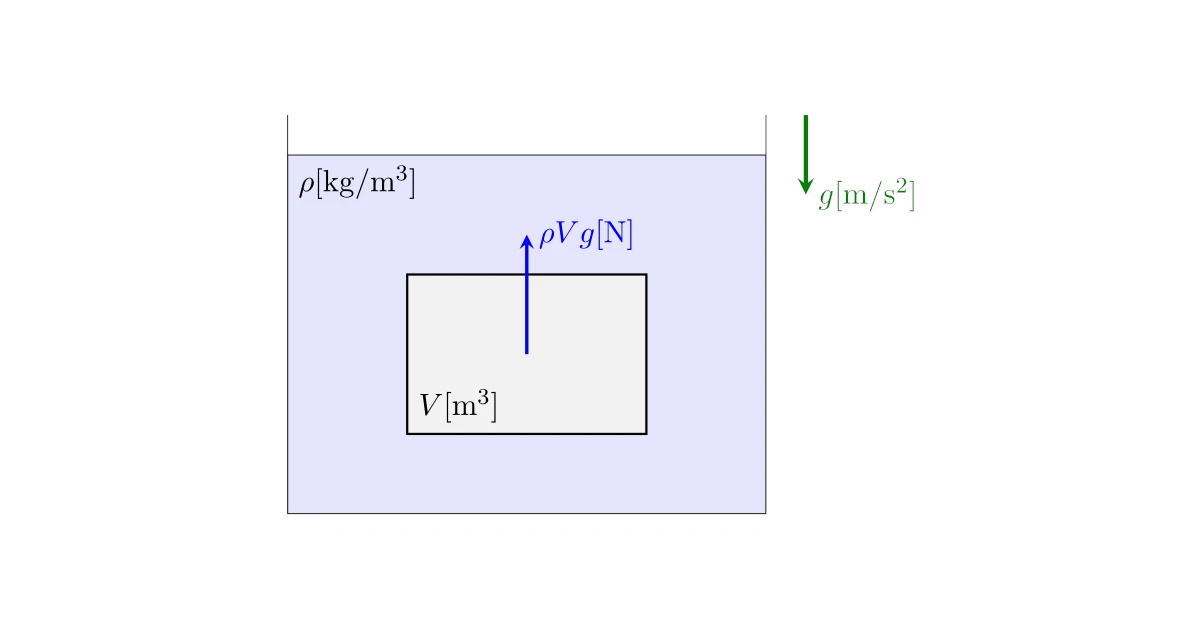
重力加速度を$g[\mrm{m/s^2}]$とする.密度$\rho[\mrm{kg/m^3}]$の液体に体積$V[\mrm{m^3}]$の物体が全て液面下に沈んでいるとき,物体に鉛直上向きに$\rho Vg[\mrm{N}]$の力がはたらく.
面白いのは浮力の公式において物体に関する情報は体積$V[\mrm{m^3}]$のみだという点です.
つまり,浮力の大きさに物体の素材は全く関係なく,体積が同じであれば(木片を沈めても鉄球を沈めても)浮力の大きさは同じです.
ここで次の疑問が浮かぶ人も少なくないかも知れません.
同じ体積の木片と鉄球を沈めたとき,両者にはたらく浮力の大きさは等しい.
しかし,木片は水に浮くが,鉄球は水に沈む.これはなぜか?
答えは次のようになります.
「木片にはたらく浮力」と「木片にはたらく重力」,「鉄球にはたらく重力」と「鉄球にはたらく浮力」をそれぞれ比べると,
- $(\text{木片にはたらく重力})<(\text{木片にはたらく浮力})$
- $(\text{鉄球にはたらく浮力})<(\text{鉄球にはたらく重力})$
となっているため,木材は浮力の方が大きく浮き,鉄球は重力の方が大きく沈む.
浮力を考えれば木片も鉄球も等しい大きさですが,重力ははるかに鉄球の方が大きいのが理由というわけですね.
アルキメデスの原理
ここで浮力の大きさに関する原理であるアルキメデスの原理を説明しておきます.
浮力の大きさの公式$\rho Vg[\mrm{N}]$について,液体の密度は$\rho[\mrm{kg/m^3}]$で物体が液面下に体積$V[\mrm{m^3}]$沈んでいますから,$\rho V[\mrm{kg}]$は物体が押しのけた液体の質量ですね.
したがって,これに重力加速度$g[\mrm{m/s^2}]$をかけてできる$\rho Vg[\mrm{N}]$は「物体が押しのけた分の液体にはたらく重力」ということができます.
実はこれがアルキメデスの原理で,次のようにいうことができます.
[アルキメデスの原理] 物体が流体中にあるとき,物体には「物体が押しのけた分の流体にはたらく重力」と同じ大きさの浮力がはたらく.
このアルキメデスの原理を踏まえると,完全に物体が沈んでいない場合には沈んだ分の体積を$V[\mrm{m^3}]$として考えればいいことが分かりますね.
浮力の例
それでは具体例を考えましょう.
物体が液体に浮かんでいる場合
重力加速度を$g[\mrm{m/s^2}]$とし,密度$\rho[\mrm{kg/m^3}]$の液体に質量$m[\mrm{kg}]$の物体を液面上に浮かべると静止したとする.
このとき,物体が液面下に沈んでいる部分の体積$V[\mrm{m^3}]$を求めよ.
アルキメデスの原理から,液面下に沈んでいる体積$V[\mrm{m^3}]$の部分だけに浮力がはたらきます.
したがって,物体が液面下に沈んでいる体積を$V[\mrm{m^3}]$とすると,物体には
- 大きさ$\rho Vg[\mrm{N}]$の浮力
- 大きさ$mg[\mrm{N}]$の重力
がはたらいています.
いま物体は静止しているので,これらの力がつり合っています.
すなわち,鉛直上向きの浮力と鉛直下向きの重力の合力は$0$なので,
となります.よって,物体の液面下に沈んでいる部分の体積が$\frac{m}{\rho}[\mrm{m^3}]$であると分かりました.
物体が液体中に沈んでいる場合1
重力加速度を$g[\mrm{m/s^2}]$とし,密度$\rho[\mrm{kg/m^3}]$の液体に体積$V[\mrm{m^3}]$,質量$m[\mrm{kg}]$の物体を液面下に完全に沈める.
$m>\rho V$のとき,物体がどのような運動をし始めるか答えよ.ただし,水の抵抗は無視する.
物体には
- 大きさ$\rho Vg[\mrm{N}]$の浮力
- 大きさ$mg[\mrm{N}]$の重力
がはたらいています.
浮力は鉛直上向き,重力は鉛直下向きにはたらいているので,物体にはたらく力の合力は鉛直下向きに$mg-\rho Vg[\mrm{N}]=(m-\rho V)g[\mrm{N}]$となります.
いま$m>\rho V$なので$(m-\rho V)g>0$となり,物体は沈んでいくことが分かりますね.
鉛直下向きに大きさ$(m-\rho V)g[\mrm{N}]$の力がはたらきます.
このときの鉛直下向きで大きさ$a$の加速度で運動するとすると,運動方程式より
となります.よって,加速度$\bra{g-\dfrac{\rho V}{m}g}[\mrm{m/s^2}]$で鉛直下向きに等加速度直線運動を始めることが分かりました.
もし浮力がない状態を考えれば物体は自由落下で加速度は$g[\mrm{m/s^2}]$です.
今回の結果の$a=\bra{g-\dfrac{\rho V}{m}g}[\mrm{m/s^2}]$は浮力があることによって,加速度が$\dfrac{\rho V}{m}g[\mrm{m/s^2}]$だけ弱められていると解釈できますね.
ただし,現実的には液体の抵抗は無視できず等加速度直線運動にはなりませんが,「動きはじめ」などは液体の抵抗が小さく無視できると考えれば,ほぼ等加速度直線運動をし始めるとみなすことができます.
物体が液体中に沈んでいる場合2
重力加速度を$g[\mrm{m/s^2}]$とし,密度$\rho[\mrm{kg/m^3}]$の液体に体積$V[\mrm{m^3}]$,質量$m[\mrm{kg}]$の物体を液面下に完全に沈める.
$m<\rho V$のとき,物体がどのような運動をし始めるか答えよ.ただし,水の抵抗は無視する.
上の例と同様に,物体には
- 大きさ$\rho Vg[\mrm{N}]$の浮力
- 大きさ$mg[\mrm{N}]$の重力
がはたらいているので,物体にはたらく力の合力は鉛直下向きに$mg-\rho Vg[\mrm{N}]=(m-\rho V)g[\mrm{N}]$となります.
今度は不等号が逆向きになったので,物体は浮き上がっていくことが分かりますね.
鉛直上向きに大きさ$(\rho V-m)g[\mrm{N}]$の力がはたらきます.
このときの鉛直下向きで大きさ$a$の加速度で運動するとすると,運動方程式より
となります.よって,加速度$\bra{\dfrac{\rho V}{m}g-g}[\mrm{m/s^2}]$で鉛直上向きに等加速度直線運動を始めることが分かりました.
もし重力がない状態を考えれば物体は大きさ$\dfrac{\rho V}{m}g[\mrm{m/s^2}]$の加速度で上昇していきます.
今回の結果の$a=\bra{\dfrac{\rho V}{m}g-g}[\mrm{m/s^2}]$は重力があることによって,加速度が$g[\mrm{m/s^2}]$だけ弱められていると解釈できますね.
ただし,現実的には液体の抵抗は無視できず等加速度直線運動にはなりませんが,「動きはじめ」などは液体の抵抗が小さく無視できると考えれば,ほぼ等加速度直線運動をし始めるとみなすことができます.
コメント