物理の大きな目的の1つに「未来の予測」があります.
たとえば,宇宙に人工衛星を打ち上げるとき,どのような向きにどれくらいの力で人工衛星を飛ばせば地球の周回軌道に乗せられるかといったことも未来の予測です.
このように物理で未来の予測を行う際,どのような力がはたらいているのかを把握することが重要になります.
力がどのようにはたらくかを考える分野を力学といいますが,特に高校物理の力学では「重力」「垂直抗力」「摩擦力」「張力」「弾性力」「浮力」の6種類の力が基本的なものとして扱われます.
この記事では,
- 力の考え方の基本
- 基本の6種類の力
を順に説明します.
「力学の基本」の一連の記事
力の考え方の基本
力の基本として,
- 力の3要素
- 力の大きさの単位
を説明しておきます.
力の3要素
力を考えるときには,
- 大きさ
- 向き
- 作用点
の3つを考えることが非常に大切で.これら3つを併せて力の3要素といいます.
言い換えれば「『どの点』に『どれくらいの大きさ』の力が『どの向き』にはたらいているのか」という情報が力の3要素というわけですね.
力の大きさの単位
一般に力の大きさの単位は$\mrm{N}$(ニュートン)を用いることが多いです.
イメージとしては「手にりんごを乗せたときに,りんごから受ける力」がだいたい$1\mrm{N}$です.
地球上で$102\mrm{g}$の物体にはたらく重力の大きさが約$1\mrm{N}$です.
厳密には質量$1\mrm{kg}$の物体に加速度$1\mrm{m/s^2}$を与える力が$1\mrm{N}]$で
- 質量の単位:キログラム$\mrm{kg}$
- 長さの単位:メートル$\mrm{m}$
- 時間の単位:秒$\mrm{s}$
を用いて
で表されます.
このことは,のちに運動方程式を学ぶとより良く理解できるようになります.
基本の6種類の力
それでは,基本の6種類の力「重力」「垂直抗力」「摩擦力」「張力」「弾性力」「浮力」をそれぞれ簡単にまとめていきましょう.
重力
この宇宙の全ての質量を持つ物質は互いに引き寄せ合い,この互いに引き付け合う力を万有引力と呼びます.
互いの物質の質量が大きいほど万有引力は大きくなりますが,数百キロ,数トンレベルの質量では()無視できる程度でしかありません.
しかし,質量が星レベルになると万有引力は無視できない大きさになります.例えば,我々が地球上に立てるのは,地球と私たちの体が万有引力で引き付け合っているからですね.
このような星レベルの万有引力を重力と呼びます.
重力加速度を$g[m/s^2]$とする.質量$m[kg]$の物質にかかる重力は
- 大きさ:$mg[\mrm{N}]$
- 向き:鉛直下向き
- 作用点:物体の重心
である.
また,鉛直下向きとは「地球の中心に向かう向き」のことをいいます.
もう少しざっくり言えば「真下」ということですね.
質量$m$は物質によって変わり,例えば
- 質量が2倍になれば重力も2倍に
- 質量が半分になれば重力も半分に
なります.このことは直感的にも合っていることだと思います.
垂直抗力
接触している物体からまっすぐ押し返される力を垂直抗力と呼びます.
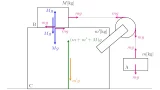
上図では$\ve{N}$と$\ve{N’}$はいずれも垂直抗力で,垂直抗力については次の事実が大切です.
垂直抗力2つの物体の間にはたらく2つの垂直抗力は,向きが逆で大きさは等しい.
つまり,上の図では$\ve{N}=-\ve{N’}$が成り立つというわけですね.この事実から垂直抗力は状況によって変化することが分かりますね.
垂直抗力は多くの場合で
から求めることができます.
初めのうちはよく垂直抗力を忘れがちですが,物体が接触している場合ときに垂直抗力を気にする癖をつけると間違えにくくなります.
張力
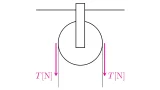
それほど弾力のない糸が物体を引く力を張力と呼びます.
上図では$\ve{T}$が物体Aにはたらく張力,$\ve{T’}$が物体Bにはたらく張力です.
張力も垂直抗力と同じく,多くの場合で
などから求めます.張力については,次の事実が大切です.
ピンと張られた糸の両端で張力の大きさは等しく,向きは逆向きである.
この事実から,上の$\ve{T}$と$\ve{T’}$の間には$\ve{T}=-\ve{T’}$の関係が成り立ちます.
また,滑車に糸を通した場合の張力を考えることも多いです.この場合については,以下の記事で具体例を用いて説明しています.
摩擦力
物体が滑るような力が与えられたとき,物体の滑りを妨げるようにはたらく力を摩擦力と呼びます.
上図では
- $\ve{F}$を動かす力
- $\ve{f}$が摩擦力
となっています.摩擦力は物体が動いているときと,静止しているときで大きさの様子が異なります.
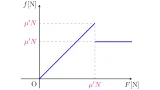
物体は滑る物体との間に大きさ$N[\mrm{N}]$の垂直抗力がはたらいているし,滑る方向に大きさ$F[\mrm{N}]$の力を加える.このとき,摩擦力の大きさを$f[\mrm{N}]$とする.
このとき,
- 物体が静止していれば$f=F$
- 物体が動いていれば$f$は速度によらず一定
である.
物体が動いているとき,物体を速く動かそうがゆっくり動かそうが摩擦力が一定であることに注意してください.
物体が動いている時の摩擦力の大きさ$f$は$f=\mu’N$と表され,$\mu’$を動摩擦係数と呼びます.
また,物体が動かないギリギリのときの摩擦力の大きさ$f[\mrm{N}]$のことを最大静止摩擦力といい,$f=\mu N$と表さすときの$\mu$を静止摩擦係数と呼びます.
動摩擦係数$\mu’$,静止摩擦係数$\mu$はいずれも摩擦力がはたらく2物体の相性のみによって決まります.
このように,摩擦力は
- 物体が静止しているとき
- 物体が静止しているギリギリのとき
- 物体が運動しているとき
の3パターンを使い分けることがポイントとなります.
弾性力
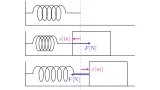
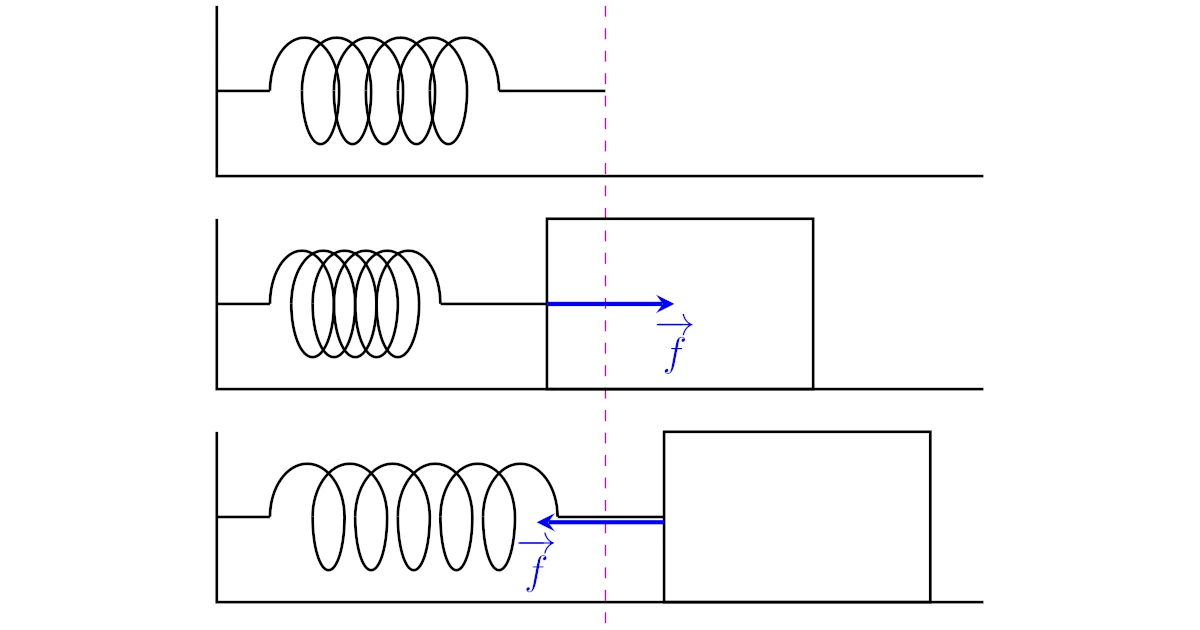
バネを水平な場所に置くとある長さで静止しますが,この長さをそのバネの自然長と呼びます.
バネは自然長より短くなると伸びようとする向きに力がはたらき,反対に自然長より長くなると縮もうとする向きに力がはたらきます.
このようにバネなどが物体を引き戻したり,押したりする力のことを弾性力と呼びます.
上図では$\ve{f}$が弾性力です.弾性力の大きさは次のフックの法則をもとに求めることができます.
[フックの法則]バネの弾性力の大きさ$F[\mrm{N}]$は,バネの自然長からの長さの変化$x[\mrm{m}]$に比例する.すなわち,$F=kx$が成り立つ.
このときの比例定数$k[\mrm{N/m}]$をバネ定数と呼び.
バネ定数$k$が大きいと,少しの伸び縮み$x$で大きな弾性力が得られます.つまり,押し返す力/引き戻す力が硬いバネほど,バネ定数が大きいといえますね.
この意味で,バネ定数はバネの「強さ」ということができますね.
浮力
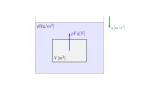
例えば,水に木片を放り込むと木片は水に浮かびます.このように流体(液体や気体)が物体を押し上げる力のことを浮力と呼びます.
さて,液体に物体を沈めるとき,浮力は以下のようになります.
[液体中の浮力]重力加速度を$g[\mrm{m/s^2}]$とする.密度$\rho[\mrm{kg/m^3}]$の液体に物体を沈める.体積$V[\mrm{m^3}]$の物体が全て液面下に沈んでいるとき,物体が液体から受ける浮力の大きさは$\rho Vg[\mrm{N}]$である.
また,「浮力」の向きは鉛直上向きです.
$\rho$はギリシャ文字で「ロー」と読みます.
液体の密度は$\rho[kg/m^3]$で,物体が体積$V[m^3]$沈んでいるので,$\rho V[kg]$は物体が押しのけた液体の質量です.
したがって,$\rho Vg[\mrm{N}]$は「物体が押しのけた液体にはたらく重力」に等しいく,この事実はアルキメデスの原理と呼ばれます.
[アルキメデスの原理]物体が流体中にあるとき,「物体が押しのけた流体の重さ」と同じ大きさの力を受ける.
アルキメデスの原理を知っていれば,液体中の浮力の公式は覚えていなくてもすぐに自分で導けますね.
コメント