次のことは当たり前ですね?
4つの巣に5羽の鳩が集まっているとき,どこかの巣には鳩が2羽以上いる.
より一般に「巣より鳩の方が多いとき,どこかの巣には鳩が2羽以上いる」といえますね.
この論法のことを数学では鳩の巣原理といいます.鳩の巣原理の他に引き出し原理やディリクレ(Dirichlet)の箱入れ原理ということもあります.
当たり前すぎて「定理というほどのことか?」と訝しむ人もいらっしゃるかもしれませんが,適切に用いればあっという間に解けてしまう問題も少なくありません.
高校数学ではそれほど積極的に学ぶ機会のない定理ではありますが,大学受験の数学にも出ることもあるので一度は触れておきたい話題のひとつです.
数学オリンピックでは鳩の巣原理を用いる問題は頻出です.
この記事では
- 鳩の巣原理とは何か?
- 鳩の巣原理を用いて解ける問題の例
を順に説明します.
鳩の巣原理とは?
冒頭で述べたことを,もう少しきちんと表現すると次のようになりますね.
[鳩の巣原理]$m$, $n$を正の整数とする.$m$個の対象を$n$組に分けるとき,$n<m$なら少なくとも1つの組には対象が2個以上属する.
「鳩の巣原理」という名前を意識すると,「$m$羽の鳩を$n$個の巣に集めるとき,$m>n$なら少なくとも1つの巣には鳩が2羽いる」ということになりますね.
鳩以外の具体例を挙げるなら,人の血液型はA型,B型,AB型,O型の4種類なので,5人いれば少なくとも1つの血液型には2人以上属していることになりますね.
このように,鳩の巣原理は「ペアの存在を示す問題」に使えそうな定理だと分かりますね.
このタイプの鳩の巣原理が最も簡単なものですが,もう少し発展させた次の定理も成り立ちますね.
[鳩ノ巣原理(発展)]$m$, $n$, $k$を正の整数とする.$m$個の対象を$n$組に分けるとき,$kn<m$なら少なくとも1つの組には対象が$k+1$個以上属する.
例えば,9人いれば少なくとも1つの血液型には3人以上属していることになりますが,これは発展版の鳩の巣原理の$k=2$の場合になっていますね.
鳩の巣原理の具体例
それでは,鳩の巣原理の威力を見て頂きましょう.
問題1
1辺の長さが$10$の正方形の内部に10個の点を任意に取る.この10個の点からうまく2点を選べば2点間の距離を$5$未満とできることを示せ.
この問題を「距離が$5$未満となるような2点が少なくとも1組存在することを示せ」と読み替えれば,「ペアの存在証明」ですから鳩の巣原理が使えないか考えましょう.
この問題で10個の点でペアを作ることになるので
「10個の点を9個のグループに分けて,このうちのどれか1グループには2個の点が存在する」
という方針を採りましょう.
つまり,正方形を9個に分割すればどんな分け方であっても,その分割の少なくとも1つの中には2個の点が存在することになりますね.
曲線で分割したりギザギザな折れ線で分割したり,正方形の分割はいろいろ考えられますが,一番自然な方法は各辺を3等分して9つの小正方形に分割する方法でしょう.
この分割では,1つの小正方形の対角線の長さは$\dfrac{10\sqrt{2}}{3}$です.
1つの長方形の中の2点が最も離れるのは向かい合う頂点にあるときなので,$\dfrac{10\sqrt{2}}{3}<5$を示せばよいですね.
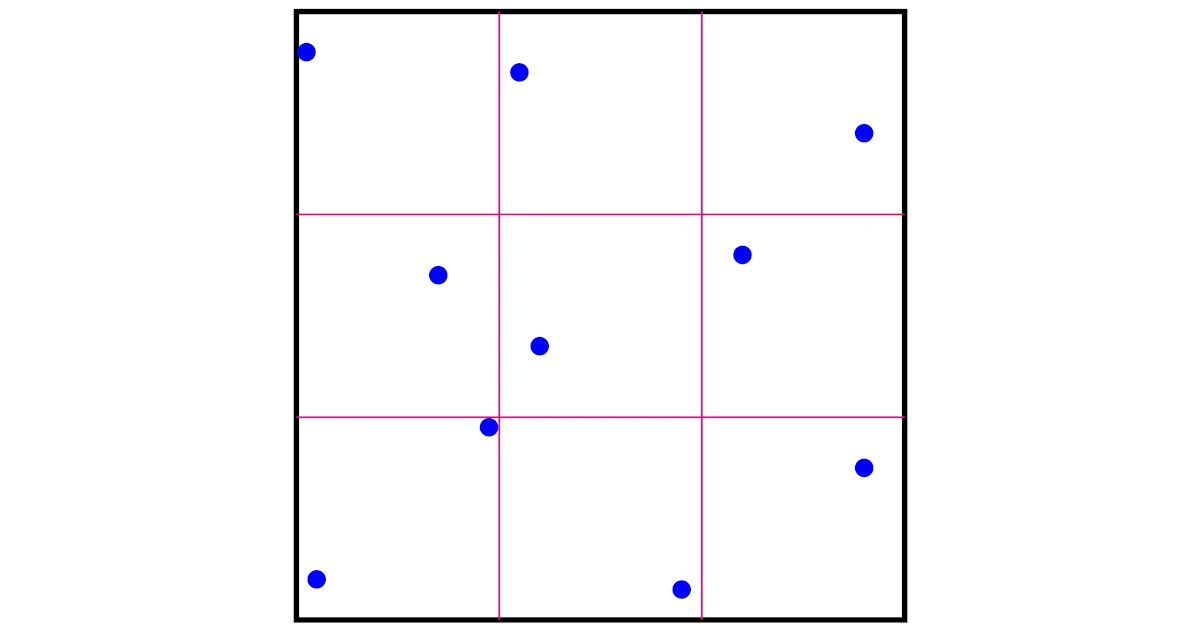
正方形を図のように合同な9個の小正方形に分割する.
このとき,鳩の巣原理により9個の小正方形のいずれか1個は周及び内部に2個の点を含む.この小正方形をAとする.
小正方形Aの周および内部にある2点間の距離が最大となるのは2点が向かい合う頂点にあるときであり,小正方形Aの1辺の長さは$\dfrac{10}{3}$なので,対角線の長さは$\dfrac{10\sqrt{2}}{3}$である.
だから,Aの対角線の長さは$5$未満なのでAに含まれる2点を選べば,この距離は$5$以下である.
問題2
少し難しい問題も考えておきます.
正の整数$n$に対して,$1$以上$2n$以下の$n+1$個の整数を考える.このとき,一方の整数が他方の整数を割り切るような2整数が存在することを示せ.
$n+1$個の整数の中に,一方の整数が他方の整数を割り切るような整数のペアが存在することを示すので,鳩の巣原理を使う場合には「巣」を$n$個用意することになります.
ここでポイントになるのは
- 1以上$2n$以下の$2n$個の整数の中には,$n$個の奇数が存在する.
- もし自然数$k$が自然数$\ell$を割り切るとき,$k$に含まれる重複を含めた素因数は$\ell$の素因数としても含まれる.
の2つです.
1つ目のポイントから,$n+1$個の整数を奇数になるまで2で割ってできた$n+1$個の奇数の中には等しい奇数$a$, $b$ ($a=b$)が存在します.
2つ目のポイントから,この等しい2つの奇数$a$, $b$の2で割る前のもとの自然数は,素因数2の個数だけが違うので,一方が他方を割り切ることになりますね.
$1$以上$2n$以下の$n+1$個の整数を全て奇数になるまで$2$で割ると,「$n+1$個の奇数」$\dots(*)$ができる.
$1$以上$2n$以下の奇数は全部で$n$個存在するから,鳩の巣原理より$(*)$の中に等しい2つの奇数$a$, $b$ ($a=b$)が存在する.
この等しい奇数$a$, $b$を$2$で割る前の整数は,それぞれ$2^{k}\cdot a$, $2^{\ell}\cdot b$と表せる.
$a$, $b$は対称だから$k\geqq\ell$としてよく,このとき$a=b$より
となる.$2^{k-\ell}$は整数だから,$2^{\ell}\cdot b$は$2^{k}\cdot a$を割り切る.
以上より,題意が従う.
コメント