座標のある$xy$平面上や$xyz$空間上のベクトルは成分で表すことができるのでした.
しかし,座標のない平面上や空間上でベクトルを考えるときは,成分で表せないので少し不便に感じることがあります.
そこで座標のない平面上や空間上にも原点$\mrm{O}$のような点を考えることで,見通しよくベクトルが計算できることがあります.
この記事では
- 位置ベクトルとは何か?
- 内分・外分・三角形の重心の公式
を順に説明します.
「ベクトル」の一連の記事
位置ベクトルとは何か?
$xy$平面上の原点$(0,0)$を$\mrm{O}$とし,$xy$平面上の点$\mrm{P}(a,b)$を考えると,原点$\mrm{O}$から点$\mrm{P}$へ向かうベクトル$\ve{p}$は$\ve{p}=\pmat{a\\b}$となります.
もともと原点を考えない平面上や空間上であっても,「原点に相当する点$\mrm{O}$」を決めて点$\mrm{O}$を始点とするベクトルを考えると便利なことがよくあり,このベクトルを位置ベクトルといいます.
点$\mrm{O}$と点$\mrm{P}$を考える.このとき,$\Ve{OP}$を「点$\mrm{O}$を基準とする点$\mrm{P}$の位置ベクトル」という.
また,点$\mrm{P}$の位置ベクトルが$\ve{p}$のとき,$\mrm{P}(\ve{p})$と表す.
基準とする点$\mrm{O}$をとくに気にしないことも多く,そのときは単に「点$\mrm{P}$の位置ベクトル」といいます.
基準とする点$\mrm{O}$は原点の気持ちです.
そのため,位置ベクトルが$\ve{p}$の点$\mrm{P}$を$\mrm{P}(\ve{p})$と表すのは,座標$(a,b)$の点$\mrm{P}$を$\mrm{P}(a,b)$と表すのと同じ感覚です.
内分・外分・三角形の重心の公式
次に内分・外分・三角形の重心の位置ベクトルを説明します.
内分の位置ベクトル
2点$\mrm{A,B}$の位置ベクトルをそれぞれ$\ve{a}$, $\ve{b}$とする.このとき,線分$\mrm{AB}$を$m:n$に内分する点$\mrm{P}$の位置ベクトル$\ve{p}$は
と表せる.
ベクトルの内分公式と同様の形をしていますね.証明も同様なので省略します.
外分の位置ベクトル
2点$\mrm{A,B}$の位置ベクトルをそれぞれ$\ve{a}$, $\ve{b}$とする.このとき,線分$\mrm{AB}$を$m:n$に外分する点$\mrm{Q}$の位置ベクトル$\ve{q}$は
と表せる.
ベクトルの外分公式と同様の形をしていますね.証明も同様なので省略します.
三角形の重心の位置ベクトル
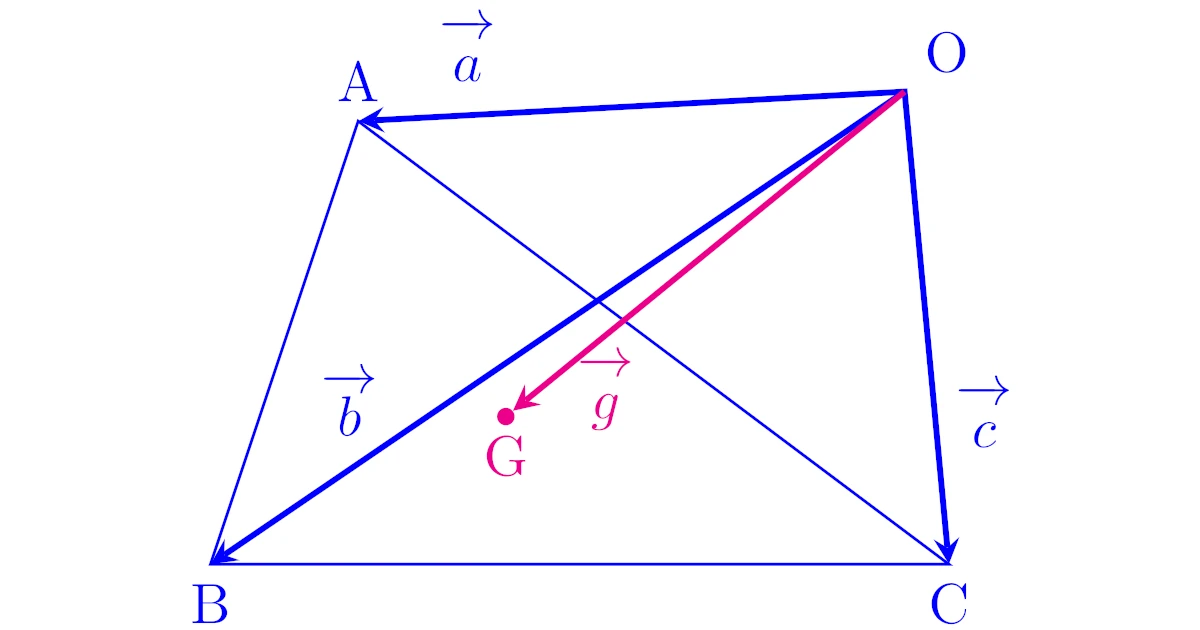
同一直線上にない3点$\mrm{A,B,C}$の位置ベクトルをそれぞれ$\ve{a}$, $\ve{b}$, $\ve{c}$とする.このとき,$\tri{ABC}$の重心$\mrm{G}$の位置ベクトル$\ve{g}$は
と表せる.
ベクトルの三角形の重心公式はひとつの頂点を基準として考えていましたが,位置ベクトルでは3頂点は対等なので$\ve{a}$, $\ve{b}$, $\ve{c}$が対称な式になっていますね.
コメント