ベクトル方程式｜直線と平面の具体例から考え方を理解する

図形と方程式の分野で学ぶように，$xy$平面上のグラフの方程式とはグラフ上の点$(x,y)$が満たす等式のことをいうのでした．

同様に図形$C$上の点の位置ベクトル$\ve{p}$が満たす等式のことを，$C$のベクトル方程式といいます．

ベクトル方程式の考え方を身に付けると便利なことも多く，例えば次のような問題も簡単に解くことができます．

$xyz$空間において，点$\mrm{P}(2,2,1)$を通り，ベクトル$\ve{n}=\pmat{1\\2\\-1}$に垂直な平面$\alpha$の方程式を求めよ．

この記事では，

グラフを表す方程式
ベクトル方程式の考え方
ベクトル方程式の具体例

を説明します．

「ベクトル」の一連の記事

グラフを表す方程式
ベクトル方程式の考え方
ベクトル方程式の具体例
1. 例１（通る点と法線ベクトルが分かっている場合）
2. 例１（通る点と方向ベクトルが分かっている場合）
ベクトル方程式の応用

グラフを表す方程式

ベクトル方程式の考え方を説明するために，まずは図形と方程式の分野の図形を表す方程式の考え方を復習しましょう．

次の問題は図形と方程式の分野の基本問題ですね．

$xy$平面上の２点$\mrm{A}(-2,0)$, $\mrm{B}(1,0)$に対して，$\mrm{AX}:\mrm{BX}=2:1$となる点$\mrm{X}$が描くグラフを表す方程式を求めよ．

$xy$平面上の点$\mrm{X}$が描く図形の方程式を求めたいときには，図形上の点$\mrm{X}$の座標を$(x,y)$とおいて$x$と$y$の関係式を求めれば良かったことを思い出しておきましょう．

点$\mrm{X}$の座標を$(x,y)$とする．$\mrm{BX}>0$, $\mrm{AX}>0$なので

$\begin{align*}\mrm{AX}:\mrm{BX}=2:1 \iff& \mrm{AX}=2\mrm{BX} \iff \mrm{AX}^2=4\mrm{BX}^2 \\\iff& \{x-(-2)\}^2+y^2=4\{(x-1)^2+y^2\} \\\iff& 0=3x^2-12x+3y^2 \\\iff& 4=(x-2)^2+y^2\end{align*}$

となる．よって，点$\mrm{X}$が描く図形の方程式は$4=(x-2)^2+y^2$である（点$(2,0)$中心，半径２の円の方程式を描く）．

ベクトル方程式の考え方

上の図形と方程式の問題では，グラフ上の点$(x,y)$をとり$x,y$が満たす（必要十分な）等式を求めました．このように，座標が入っている$xy$平面上では成分を用いた計算により方程式が得られます．

しかし，図形には必ずしも座標が考えられているとは限らないので，そのような場合は別の方法をとることになります．

そこで図形上の点を$(x,y)$とおく代わりに，図形上の点の位置ベクトルを$\ve{x}$とおいたときの$\ve{x}$が満たす等式をベクトル方程式といいます．

上の図形と方程式の問題をベクトル方程式の問題に書き換えると次のようになります．

平面上の２点$\mrm{A}$, $\mrm{B}$の位置ベクトルをそれぞれ$\ve{a}$, $\ve{b}$とする．$\mrm{AX}:\mrm{BX}=2:1$となる点$\mrm{X}$が描く図形のベクトル方程式を$\ve{a}$, $\ve{b}$で表せ．

図形と方程式の時に図形上の点$\mrm{X}$の座標$(x,y)$を考えたのと同様に，ベクトル方程式では点$\mrm{X}$の位置ベクトル$\ve{x}$を考えます．

点$\mrm{X}$の位置ベクトルを$\ve{x}$とする．

$\begin{align*}|\Ve{AX}|:|\Ve{BX}|=2:1 &\iff|\mrm{AX}|=2|\Ve{BX}| \\&\iff|\ve{x}-\ve{a}|=2|\ve{x}-\ve{b}|\end{align*}$

となる．

ベクトルの大きさは常に正なので，最後の等式を２乗して

$\begin{align*}|\ve{x}-\ve{a}|^2=4|\ve{x}-\ve{b}|^2\end{align*}$

を答えにしても構いません．

$\ve{x}-\ve{a}|=k|\ve{x}-\ve{b}|$ ($k>0$)の形のベクトル方程式はよく現れるので，このベクトル方程式が円を表すことは知っておくとよいでしょう．

ベクトル方程式の具体例

もう少しベクトル方程式の具体例を考えてみましょう．

例１（通る点と法線ベクトルが分かっている場合）

平面において，点$\mrm{P}(\ve{p})$を通り，零ベクトルでないベクトル$\ve{n}$に垂直な直線$\ell_1$のベクトル方程式を求めよ．

この問題の$\ve{a}$のように直線$\ell$に垂直なベクトルを，直線$\ell$の法線ベクトルと言います．

$\mrm{P}(\ve{p})$は点$\mrm{P}$の位置ベクトルが$\ve{p}$であることを表すのでした．

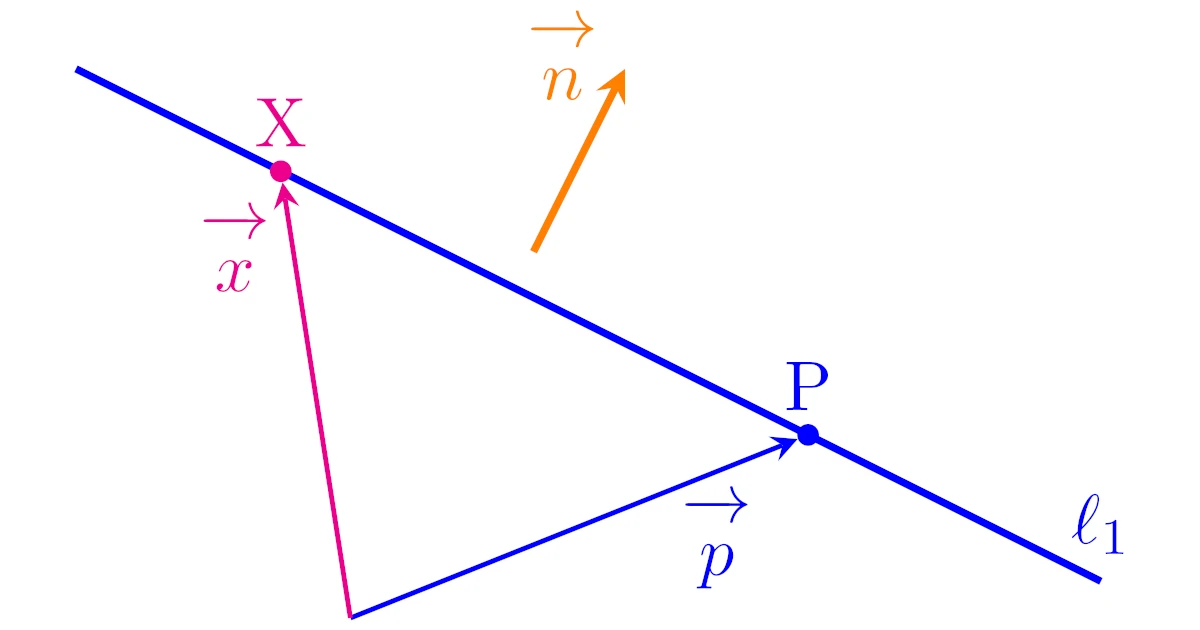
直線$\ell_1$上の任意の点$\mrm{X}$の位置ベクトルを$\ve{x}$とする．

このとき，$\Ve{PX}=\ve{x}-\ve{p}$は直線$\ell_1$に平行なベクトルまたは零ベクトルであり，直線$\ell_1$は$\ve{a}$に垂直だから，

$\begin{align*}(\ve{x}-\ve{p})\cdot\ve{n}=0\end{align*}$

が直線$\ell_1$のベクトル方程式である．

例１（通る点と方向ベクトルが分かっている場合）

平面において，点$\mrm{P}(\ve{p})$を通り，零ベクトルでないベクトル$\ve{d}$に平行な直線$\ell_2$のベクトル方程式を求めよ．

この問題の$\ve{a}$のように直線$\ell$に平行なベクトルを，直線$\ell$の方向ベクトルと言います．

直線$\ell_2$上の任意の点$\mrm{X}$の位置ベクトルを$\ve{x}$とする．

このとき，$\ve{x}-\ve{p}$は直線$\ell_2$に平行なベクトルまたは零ベクトルであり，直線$\ell_2$は$\ve{d}$に平行だから，

$\begin{align*}\ve{x}-\ve{p}=k\ve{d}\end{align*}$

となる（$k$は任意の実数）．これが直線$\ell_2$のベクトル方程式である．

ベクトル方程式の応用

ベクトル方程式は座標が入っていなくても図形を表すことができるという点で優れているわけですが，座標が入っていてももちろん扱うことができます．

以下のように座標上の問題に考えたとき，ベクトル方程式の考え方ができると便利です．

$xyz$空間において，点$\mrm{P}(2,2,1)$を通り，ベクトル$\ve{n}=\pmat{1\\2\\-1}$に垂直な平面$\alpha$の方程式を求めよ．

原点を$\mrm{O}$とする．$xyz$空間上の点$\mrm{X}(x,y,z)$について，点$\mrm{X}$が平面$\alpha$上にあることと$\Ve{PX}\cdot\ve{n}=0$を満たすことは同値である．

よって，

$\begin{align*}\Ve{PX}\cdot\ve{n}=0 &\iff (\Ve{OX}-\Ve{OP})\cdot\ve{n}=0 \\&\iff \pmat{x-2\\y-2\\z-1}\cdot\pmat{1\\2\\-1}=0 \\&\iff (x-2)+2(y-2)-(z-1)=0 \\&\iff x+2y-z-5=0\end{align*}$