ベクトルの内積の基本性質｜計算で便利な性質を総まとめ

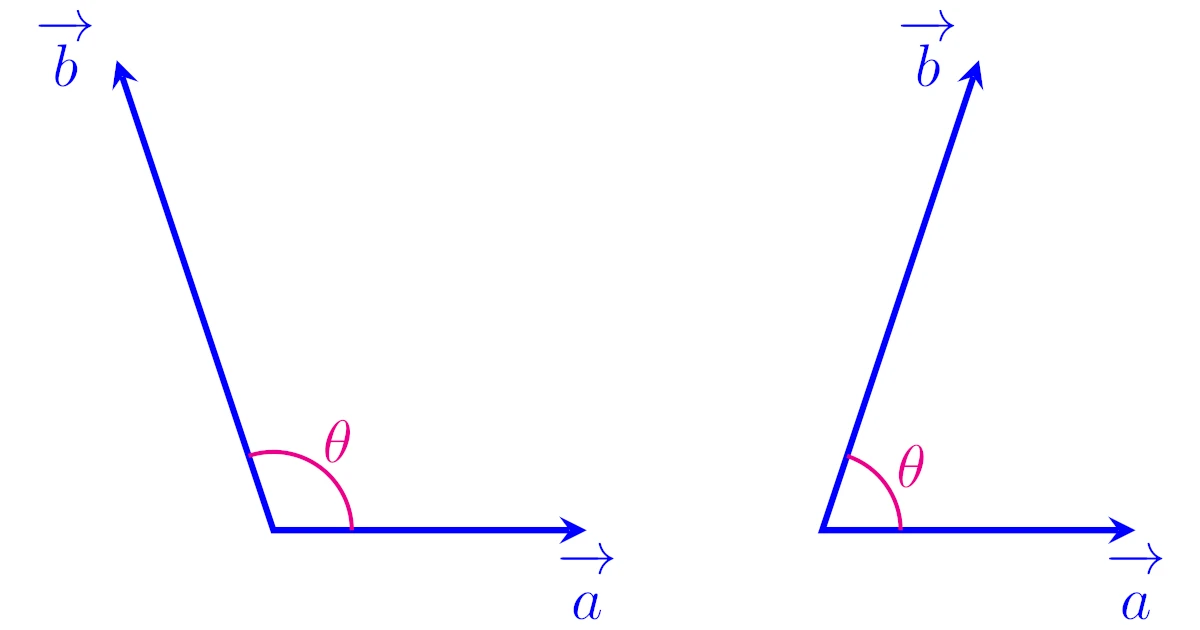
２つのベクトル$\ve{a}$, $\ve{b}$の内積は，$\ve{a}$, $\ve{b}$のなす角$\theta$を用いて

$\begin{align*}\ve{a}\cdot\ve{b}=|\ve{a}||\ve{b}|\cos{\theta}\end{align*}$

と定義されるのでした．

ベクトルの計算で内積は頻繁に現れるので，内積の性質は整理しておきたいところです．

とくに$xy$平面上の成分で表されたベクトルの内積はとても簡単に求められることは当たり前にしておきましょう．

この記事では

内積の値に関する基本性質
直交座標上の内積
内積の計算の基本性質

を順に説明します．

「ベクトル」の一連の記事

内積の値に関する基本性質
直交座標上の内積
1. 成分で表されたベクトルの内積
2. 具体例（成分で表されたベクトルのなす角）
内積の計算の基本性質

内積の値に関する基本性質

まずは内積の値に関しての基本性質を解説します．

ベクトルの長さと内積

同じベクトル$\ve{a}$と$\ve{a}$のなす角は$0^\circ$なので，ベクトルの長さ$|\ve{a}|$は以下のように内積を用いても表せます．

ベクトル$\ve{a}$に対して，$\ve{a}\cdot\ve{a}=|\ve{a}|^2$が成り立つ．

内積の定義より

$\begin{align*}\ve{a}\cdot\ve{a}=|\ve{a}||\ve{a}|\cos{0^\circ}=|\ve{a}|^2\end{align*}$

が成り立つ．

両辺で正の平方根をとれば$|\ve{a}|=\sqrt{\ve{a}\cdot\ve{a}}$とも書けますね．

内積の正負となす角の大きさ

ベクトル$\ve{a}$, $\ve{b}$が零ベクトル$\ve{0}$でなければ，$|\ve{a}|$と$|\ve{b}|$がともに正なので，内積$\ve{a}\cdot\ve{b}=|\ve{a}||\ve{b}|\cos{\theta}$の正負は$\cos{\theta}$の正負によって決まりますね．

$\theta$は$0^\circ\leqq\theta\leqq180^\circ$を動き，$\theta=90^\circ$で$\cos{\theta}$が正から負へと移りますから，以下のようにまとめることができます．

零ベクトル$\ve{0}$でないベクトル$\ve{a}$, $\ve{b}$のなす角$\theta$に対して，以下が成り立つ．

$0^\circ\leqq\theta<90^\circ$であることと，$\ve{a}\cdot\ve{b}>0$は同値
$\theta=90^\circ$であることと，$\ve{a}\cdot\ve{b}=0$は同値
$90^\circ<\theta\leqq180^\circ$であることと，$\ve{a}\cdot\ve{b}<0$は同値

このことから，ベクトルの内積を考えれば，鋭角か直角か鈍角かが判定できるわけですね．

内積のとりうる値の範囲

ベクトル$\ve{a}$, $\ve{b}$に対して，

$\begin{align*}-|\ve{a}||\ve{b}|\leqq\ve{a}\cdot\ve{b}\leqq|\ve{a}||\ve{b}|\end{align*}$

が成り立つ．

$\ve{a}$, $\ve{b}$のなす角を$\theta$とすると，内積の定義より

$\begin{align*}\ve{a}\cdot\ve{b}=|\ve{a}||\ve{b}|\cos{\theta}\end{align*}$

であり，$-1\leqq\cos{\theta}\leqq1$なので

$\begin{align*}-|\ve{a}||\ve{b}|\leqq|\ve{a}||\ve{b}|\cos{\theta}\leqq|\ve{a}||\ve{b}|\end{align*}$

である．よって，

$\begin{align*}-|\ve{a}||\ve{b}|\leqq\ve{a}\cdot\ve{b}\leqq|\ve{a}||\ve{b}|\end{align*}$

が成り立つ．

また，$\ve{a}=\ve{0}$または$\ve{b}=\ve{0}$なら全て$0$で等しく，$\ve{a}=\ve{0}$かつ$\ve{b}=\ve{0}$なら

$\begin{align*}&\ve{a}\cdot\ve{b}\leqq|\ve{a}||\ve{b}|\iff\cos{\theta}=1\iff\theta=0^\circ, \\&-|\ve{a}||\ve{b}|\leqq\ve{a}\cdot\ve{b}\iff\cos{\theta}=-1\iff\theta=180^\circ\end{align*}$

なので，

$\ve{a}\cdot\ve{b}\leqq|\ve{a}||\ve{b}|$の等号成立条件は，$\ve{a}$と$\ve{b}$が同じ向きであること
$-|\ve{a}||\ve{b}|\leqq\ve{a}\cdot\ve{b}$の等号成立条件は，$\ve{a}$と$\ve{b}$が逆向きであること

となりますね．

直交座標上の内積

$xy$平面上の成分で表されたベクトルの内積はとても簡単に計算することができます．

成分で表されたベクトルの内積

［直交座標上の内積］$xy$平面上のベクトル$\ve{a}=\pmat{a_1\\a_2}$, $\ve{b}=\pmat{b_1\\b_2}$に対して，

$\begin{align*}\ve{a}\cdot\ve{b}=a_1b_1+a_2b_2\end{align*}$

が成り立つ．

つまり，２つのベクトルの第１成分同士をかけたものと第２成分同士をかけたものを足せば，それが内積に一致するというわけですね．

$\ve{a}=\pmat{a_1\\a_2}$, $\ve{b}=\pmat{b_1\\b_2}$より

$\begin{align*}|\ve{a}|^2={a_1}^2+{a_2}^2,\quad |\ve{b}|^2={b_1}^2+{b_2}^2\end{align*}$

であり，$\ve{a}-\ve{b}=\pmat{a_1-b_1\\a_2-b_2}$より

$\begin{align*}|\ve{a}-\ve{b}|^2&=(a_1-b_1)^2+(a_2-b_2)^2 \\&=(a_1^2-2a_1b_1+b_1^2)+(a_2^2-2a_2b_2+b_2^2)\end{align*}$

である．これらを内積の展開公式$|\ve{a}-\ve{b}|^2=|\ve{a}|^2-2\ve{a}\cdot\ve{b}+|\ve{b}|^2$に代入して，

$\begin{align*}(a_1^2-2a_1b_1+&b_1^2)+(a_2^2-2a_2b_2+b_2^2) \\&=(a_1^2+a_2^2)-2\ve{a}\cdot\ve{b}+b_1^2+b_2^2\end{align*}$

であり，整理すると$\ve{a}\cdot\ve{b}=a_1a_2+b_1b_2$となる．

具体例（成分で表されたベクトルのなす角）

成分で表されたベクトルの内積が簡単に求まることから，次のような問題も解くことができますね．

$\ve{a}=\pmat{1\\3}$, $\ve{b}=\pmat{2\\-1}$に対して，$\ve{a}$と$\ve{b}$のなす角$\theta$は鋭角，直角，鈍角のどれか．

また，このときの$\cos{\theta}$を求めよ．

［直交座標上の内積］より，

$\begin{align*}\ve{a}\cdot\ve{b}&=\pmat{1\\3}\cdot\pmat{2\\-1} \\&=1\cdot2+3\cdot(-1)=-1\end{align*}$

である．よって，$\ve{a}\cdot\ve{b}$の内積は負だから，$\ve{a}$と$\ve{b}$のなす角は鈍角である．

また，

$\begin{align*}&|\ve{a}|=\sqrt{1^2+3^2}=\sqrt{10}, \\&|\ve{b}|=\sqrt{2^2+(-1)^2}=\sqrt{5}\end{align*}$

なので，内積の定義$\ve{a}\cdot\ve{b}=|\ve{a}||\ve{b}|\cos{\theta}$より

$\begin{align*}\cos{\theta}&=\frac{\ve{a}\cdot\ve{b}}{|\ve{a}||\ve{b}|} \\&=\frac{-1}{\sqrt{10}\sqrt{5}}=-\frac{1}{5\sqrt{2}}\end{align*}$

である．

内積の計算の基本性質

内積について，交換法則や分配法則といった便利な性質が成り立ちます．

ベクトル$\ve{a}$, $\ve{b}$, $\ve{c}$と実数$k$に対して，以下が成り立つ．

$\ve{a}\cdot\ve{b}=\ve{b}\cdot\ve{a}$
$k(\ve{a}\cdot\ve{b})=(k\ve{a})\cdot\ve{b}=\ve{a}\cdot(k\ve{b})$
$\ve{a}\cdot(\ve{b}+\ve{c})=\ve{a}\cdot\ve{b}+\ve{a}\cdot\ve{c}$

これらも［直交座標上の内積］の公式から証明しましょう．

ベクトル$\ve{a}$, $\ve{b}$, $\ve{c}$を$xy$平面上におき，それぞれ

$\begin{align*}\ve{a}=\pmat{a_1\\a_2},\quad \ve{b}=\pmat{b_1\\b_2},\quad \ve{c}=\pmat{c_1\\c_2}\end{align*}$

とする．

［直交座標上の内積］の公式より

$\begin{align*}&\begin{aligned}\ve{a}\cdot\ve{b}&=a_1b_1+a_2b_2 \\&=b_1a_1+b_2a_2=\ve{b}\cdot\ve{a}\end{aligned}, \\&\begin{aligned}k(\ve{a}\cdot\ve{b})&=k(a_1b_1+a_2b_2) \\&=(ka_1)b_1+(ka_2)b_2=(k\ve{a})\cdot\ve{b}, \\k(\ve{a}\cdot\ve{b})&=k(a_1b_1+a_2b_2) \\&=a_1(kb_1)+a_2(kb_2)=\ve{a}\cdot(k\ve{b})\end{aligned} \\&\begin{aligned}\ve{a}\cdot(\ve{b}+\ve{c})&=a_1(b_1+c_1)+a_2(b_2+c_2) \\&=(a_1b_1+a_2b_2)+(a_1c_1+a_2c_2) \\&=\ve{a}\cdot\ve{b}+\ve{a}\cdot\ve{c}\end{aligned}\end{align*}$