ベクトル$\ve{a}$, $\ve{b}$に対して,等式
が成り立つとき,$s=s’$, $t=t’$は成り立つでしょうか?
実は$\ve{a}$, $\ve{b}$がある条件を満たしていない場合には,必ずしも$s=s’$, $t=t’$が成り立つとは言えません.
この記事では,
- 係数比較できるための条件
- 2直線の交点の具体例
を順に解説します.
「ベクトル」の一連の記事
係数比較できるための条件
最初に結論を書いてしまいましょう.
「2つのベクトル$\ve{a}$, $\ve{b}$はともに零ベクトルでなく,平行でもない」とき,ベクトル$\ve{a}$, $\ve{b}$は一次独立であるともいいます.
この言葉を使えば,いまの定理は「$\ve{a}$, $\ve{b}$が一次独立なら係数比較ができる」と言うこともできますね.
直感的な理由
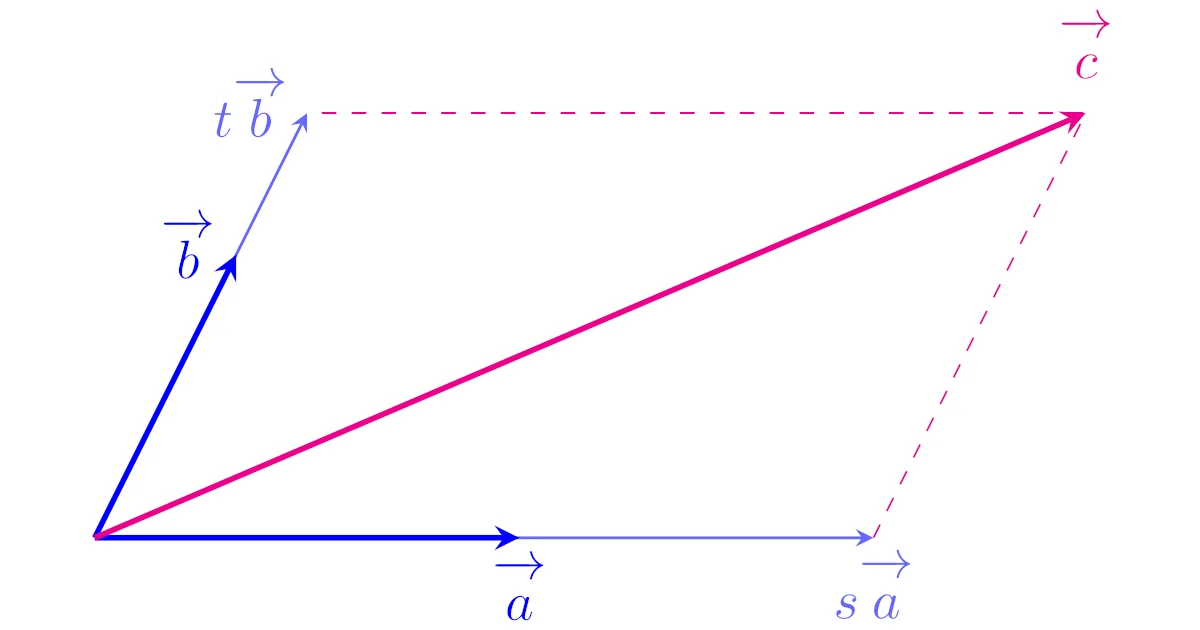
このことを直感的に理解するために,零ベクトルでない$ve{a}$, $\ve{b}$を用いて,$\ve{c}$を$\ve{c}=s\ve{a}+t\ve{b}$の形で表すことを考えます.
つまり,$\ve{a}$と$\ve{b}$をちょうど良い具合に伸ばした$s\ve{a}$と$t\ve{b}$を足し合わせて$\ve{c}$を作りたいわけですね.
このとき,$s\ve{a}$, $t\ve{b}$のどちらかの長さが少しでも違うと$s\ve{a}+t\ve{b}$が$\ve{c}$になりそうにはありませんから,$s\ve{a}+t\ve{b}=\ve{c}$となる$s$, $t$のとり方はただ1通りしかないことが見てとれます.
このことから,$\ve{a}$, $\ve{b}$が一次独立で$s\ve{a}+t\ve{b}$と$s’\ve{a}+t’\ve{b}$が等しいとき,$s$, $t$のとり方がただ1通りしかないので$s=s’$かつ$t=t’$が成り立つわけですね.
成り立たない場合
一方,零ベクトルでない$\ve{a}$, $\ve{b}$が平行なときは,必ずしも係数が一致するとは限りません.
例えば,$\ve{a}$, $\ve{b}$は平行で長さの比が$1:2$だったとしましょう.
このとき
のように,いろんな$s$, $t$に対して$s\ve{a}+t\ve{b}$が等しくなってしまいます.
このように,平行な$\ve{a}$, $\ve{b}$に対して$s\ve{a}+t\ve{b}=s’\ve{a}+t’\ve{b}$が成り立っても,必ずしも係数が等しいとは限らないわけですね.
2直線の交点の具体例
次の問題は上で見た係数比較が役に立ちます.
$\tri{ABC}$において,辺$\mrm{AB}$の中点を$\mrm{D}$,辺$\mrm{AC}$を$2:1$に内分する点を$\mrm{E}$とし,線分$\mrm{BE}$,$\mrm{C D}$の交点を$\mrm{F}$とする.
このとき,$\Ve{AF}$を$\Ve{AB}$と$\Ve{AC}$を用いて表せ.
$\mathrm{CF}:\mathrm{FD}=(1-t):t$, $\mathrm{BF}:\mathrm{FE}=(1-s):s$とおく.
このとき,$\Ve{AD}$と$\Ve{AC}$による内分の公式から
である.同様に,$\Ve{AB}$と$\Ve{AE}$による内分の公式から
である.
いま得られた$(1)$, $(2)$はどちらも$\Ve{AF}$を表しているから等しい.すなわち,
が成り立つ.$\Ve{AB}$, $\Ve{AC}$は零ベクトルでなく平行でないから,両辺で$\ve{b}$の係数と$\ve{c}$は一致するので
となる.よって,$\Ve{AF}=\dfrac{1-t}{2}\ve{b}+t\ve{c}$に$t=\dfrac{1}{2}$を代入して
を得る.
最後は$s=\dfrac{1}{4}$を$\Ve{AF}=s\ve{b}+\dfrac{2(1-s)}{3}\ve{c}$に代入しても構いません.同じ答えが得られます.
$\Ve{AF}$を$\ve{b}$と$\ve{c}$の和で2通りに表して,$\ve{b}$, $\ve{c}$が零ベクトルでなく平行でないことから係数比較できるという方法で解いたわけですね.
また,この問題はメネラウスの定理や面積比を用いた別解もよく知られており,それらの解法については以下の記事で説明しています.

コメント