小学校では「7÷3=2あまり1」のように整数の割り算の結果を商と余りを用いて表す方法を学びました.
実は多項式にも割り算があり,整数の割り算と同様の考え方で商と余りが定義されます.
多項式の割り算は次の記事で説明する因数定理などを扱う際に合わせて重要になるもので,きちんと扱えるようになっておくことが大切です.
この記事では,
- 整数の割り算
- 多項式の割り算
- 多項式の割り算の具体例
を順に解説します.
「多項式」の一連の記事
整数の割り算
小学校で習う余りを考える割り算では「7÷3=2あまり1」と表しますが,数学的にはこの=の使い方は良くありません.
この「7÷3=2あまり1」は「7は3×2よりも1大きい」と言い換えられるので,
と表すことができます.この表し方なら数学的にも扱いやすいですね.
このことをふまえて整数の割り算の商と余りをきちんと定義しましょう.
正の整数$a$, $b$に対し,
- $a=Pb+Q$
- $0\leqq Q<b$
を満たす整数$P$, $Q$をそれぞれ$a$を$b$で割った商,余りという.
(2)の$Q<b$という条件は「7÷3=1あまり4」のように余り$Q$が割る数$b$より大きくてはいけないという条件ですね.
$a\leqq0$の場合にも同様に定義できますが,簡単のため小学校の割り算に合わせて正の整数としています.
多項式の割り算
今みた整数の割り算の考え方からの類推で多項式の割り算を次のように定義します.
多項式$f(x)$と,0でない多項式$g(x)$に対し,
- $f(x)=P(x)g(x)+Q(x)$
- $(Q(x)$の次数$)<(g(x)$の次数$)$
を満たす多項式$P(x)$, $Q(x)$をそれぞれ$f(x)$を$g(x)$で割った商,余りという.
基本の計算方法
具体的に次の問題を考えてみましょう.
$x^2-x-6$を$x+1$で割ったときの商と余りを求めよ.
いま$x+1$が1次式なので
- $x^2-x-6=P(x)(x+1)+Q(x)$
- $(Q(x)$の次数$)<1$
なる$P(x)$, $Q(x)$を求めれば,それぞれ求める商,余りである.
となるから,商は$x-2$で余りは$-4$となる.
多項式$x+1$をもとにして多項式$x^2-x-6$を最高次の項から順に作っていくことで,商と余りが出来上がるわけですね.
筆算による計算方法
多項式の割り算は次のように筆算の方が計算しやすいことがあります.
$x^2-x-6$を$x+1$で割ったときの商と余りを筆算により求めよ.
以下のように筆算ができる.
よって,上に立った$x-2$が商で,下に残った$-4$が余りである.
筆算でも「多項式$x+1$をもとにして多項式$x^2-x-6$を最高次の項から順に作っていく」という考え方は上の基本の計算と同じですし,実際に同じ計算をしていることがみてとれますね.
多項式の割り算の具体例
もう少し多項式の次数を上げても同様に求められることを見ておきましょう.
具体例1(${2x^3-x^2-6}$を${x^2+x+1}$で割る)
以下の問題を基本の計算と筆算の両方で解きましょう.
$2x^3-x^2-6$を$x^2+x+1$で割った商と余りを求めよ.
基本の計算方法
基本の考え方で計算すると次のようになりますね.
よって,$2x-3$が商,$x-3$が余りです.
筆算による計算方法
筆算で計算すると次のようになりますね.
となるので,上に立った$2x-3$が商,下に残った$x-3$が余りです.
具体例2(${3x^4+x^3-2x^2+x+2}$を${x^2-x+3}$で割る)
以下の問題を基本の計算と筆算の両方で解きましょう.
$3x^4+x^3-2x^2+x+2$を$x^2-x+3$で割った商と余りを求めよ.
基本の計算方法
基本の考え方で計算すると次のようになりますね.
よって,$3x^2+4x-7$が商,$-18x+23$が余りです.
筆算による計算方法
筆算で計算すると次のようになりますね.
となるので,上に立った$3x^2+4x-7$が商,下に残った$-18x+23$が余りです.
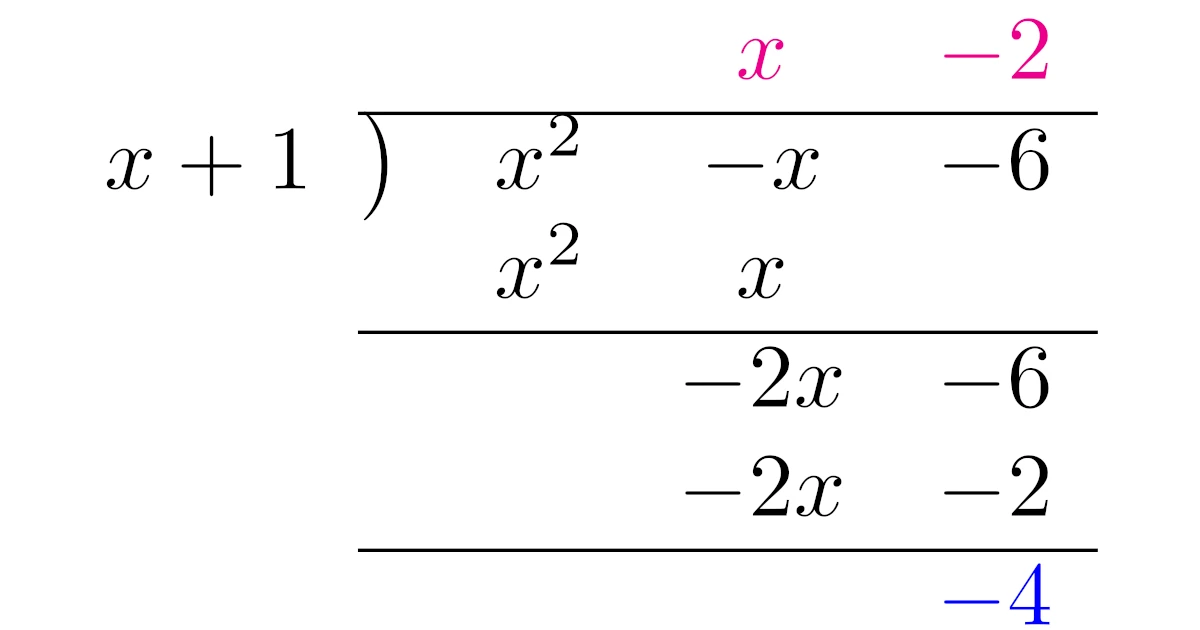
コメント