2次方程式$ax^2+bx+c=0$が解$\alpha$, $\beta$をもつとき,関係式
が成り立ちます.この2つの等式は
- 2次方程式の係数$a$, $b$, $c$
- 解$\alpha$, $\beta$
の関係式なので,(2次方程式の)解と係数の関係と呼ばれます.
解と係数の関係は覚えている必要はなく,考え方が分かっていればすぐに導くことができます.また,同様の考え方で3次以上の方程式でも解と係数の関係はすぐに導くことができます.
この記事では
- 2次方程式の解と係数の関係
- 3次以上の方程式の解と係数の関係
を順に説明します.
「多項式」の一連の記事
2次方程式の解と係数の関係
冒頭でも書いたように,2次方程式の解と係数の関係は次のようになります.
[2次方程式の解と係数の関係]$x$の2次方程式$ax^2+bx+c=0$が解$\alpha$, $\beta$をもつとき,
が成り立つ.
$\alpha$, $\beta$を2解とする2次方程式は
と表せる.これは,$x$の2次方程式$ax^{2}+bx+c=0$の両辺を$a$で割った
に一致するから,係数を比較して,
を得る.
単純に$\alpha$, $\beta$を2解とする2次方程式$(x-\alpha)(x-\beta)=0$を展開して,もとの2次方程式と係数を比較しただけなので瞬時に導けますね.
また,$a=1$の場合の解と係数の関係もよく用いるので,あえて書いておきましょう.
[2次方程式の解と係数の関係2]$x$の2次方程式$x^2+bx+c=0$が解$\alpha$, $\beta$をもつとき,
が成り立つ.
具体例1(解が2つ分かっているときの係数)
$b$, $c$を実数とする.2次方程式$2x^2+bx+c=0$の解が$\dfrac{1}{2}$,2であるとき,$b$, $c$を求めよ.
解と係数の関係より,
だから,
を得る.よって,もとの2次方程式は$2x^2-5x+2=0$である.
このように,2次方程式と解が与えられているときは,解と係数の関係を真っ先に考えたいところです.
具体例2(解が1つ分かっているときのもう1つの解と係数)
$b$を実数とする.2次方程式$x^2+bx+1=0$の解の1つが3であるとき,$b$ともう1つの解を求めよ.
もう1つの解を$\alpha$とすると,解と係数の関係より,
だから,
を得る.よって,もとの2次方程式は$x^2-\dfrac{10}{3}x+1=0$で,もう1つの解は$3$である.
具体例3(解の条件が1つ分かっているときの解と係数)
$b$を実数とする.2次方程式$x^2+bx+2=0$の一方の解が他方の解の2倍であるとする.このとき,$b$と2つの解を求めよ.
2つの解は$\alpha$, $2\alpha$とおける.解と係数の関係より,
だから,
を得る(複号同順).よって,もとの2次方程式は$x^2\mp3x+2=0$で
- $x^2-3x+2=0$のとき,解は$1$, $2$
- $x^2+3x+2=0$のとき,解は$-1$, $-2$
である.
具体例4(2次方程式の解と対称式)
2次方程式$x^2+2x+4=0$の解を$\alpha$, $\beta$とする.このとき,$\alpha^2+\beta^2$, $\alpha^2\beta+\alpha\beta^2$の値を求めよ.
解と係数の関係より
だから,
を得る.また,
を得る.
この問題の$\alpha^2+\beta^2$, $\alpha^2\beta+\alpha\beta^2$のように,$\alpha$, $\beta$を入れ替えても変わらない多項式を$\alpha$, $\beta$の対称式といいます.
一般に「$\alpha$, $\beta$の対称式は$\alpha+\beta$, $\alpha\beta$の和,差,積で表すことができる」という定理があり,このため対称式は解と係数の関係と絡めて出題されることが多いです.
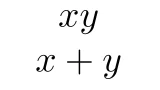
3次以上の方程式の解と係数の関係
ここまで2次方程式の解と係数の関係をみてしてきましたが,3次以上になっても同様の考え方で解と係数の関係が求まります.
そのため3次以上の解と係数の関係も一切覚える必要はなく,考え方が分かっていればすぐに導くことができます.
[3次方程式の解と係数の関係]3次方程式$ax^3+bx^2+cx+d=0$が解$\alpha$, $\beta$, $\gamma$をもつとき,
が成り立つ.
2次方程式の解と係数の関係の導出と同様に,
で右辺を展開して,
なので,係数を比較すれば3次方程式の解と係数の関係が得られます.
同様に考えれば4次方程式の解の公式,5次方程式の解の公式,……も得られますね.
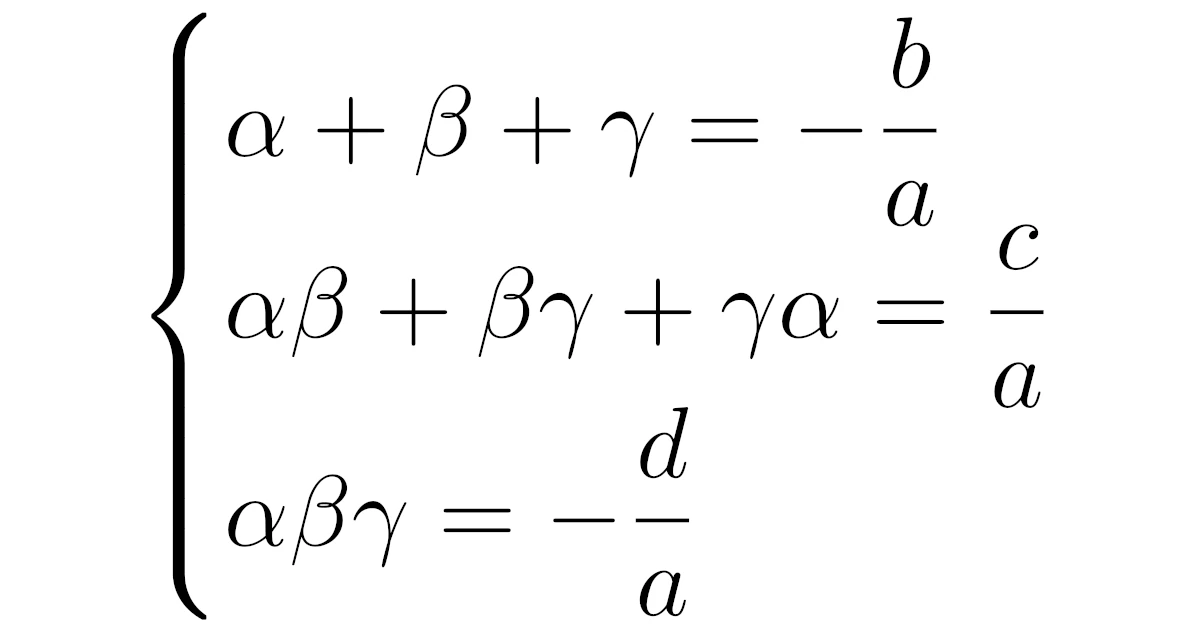
コメント